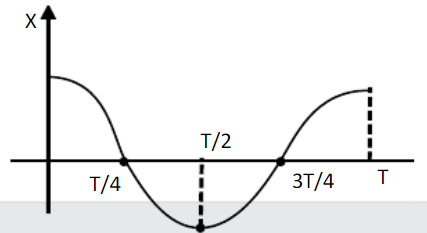
Displacement time(x-t) graph of a particle executing S.H.M is shown In the figure.The equation of S.H.M is given by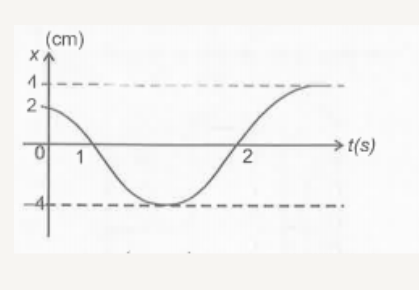

$x = 4 sin (\frac{π}{2} t + \frac{π}{6}) c m$

$x = 4 sin (π t + \frac{π}{6}) c m$

$x = 4 sin (\frac{π}{4} t + \frac{5 π}{6}) c m$

$x = 4 sin (π t + \frac{5 π}{6}) c m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video & image solution for Displacement time(x-t) graph of a particle executing S.H.M is shown In the figure.The equation of S.H.M is given by by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS MOCK TEST 9

Similar Questions

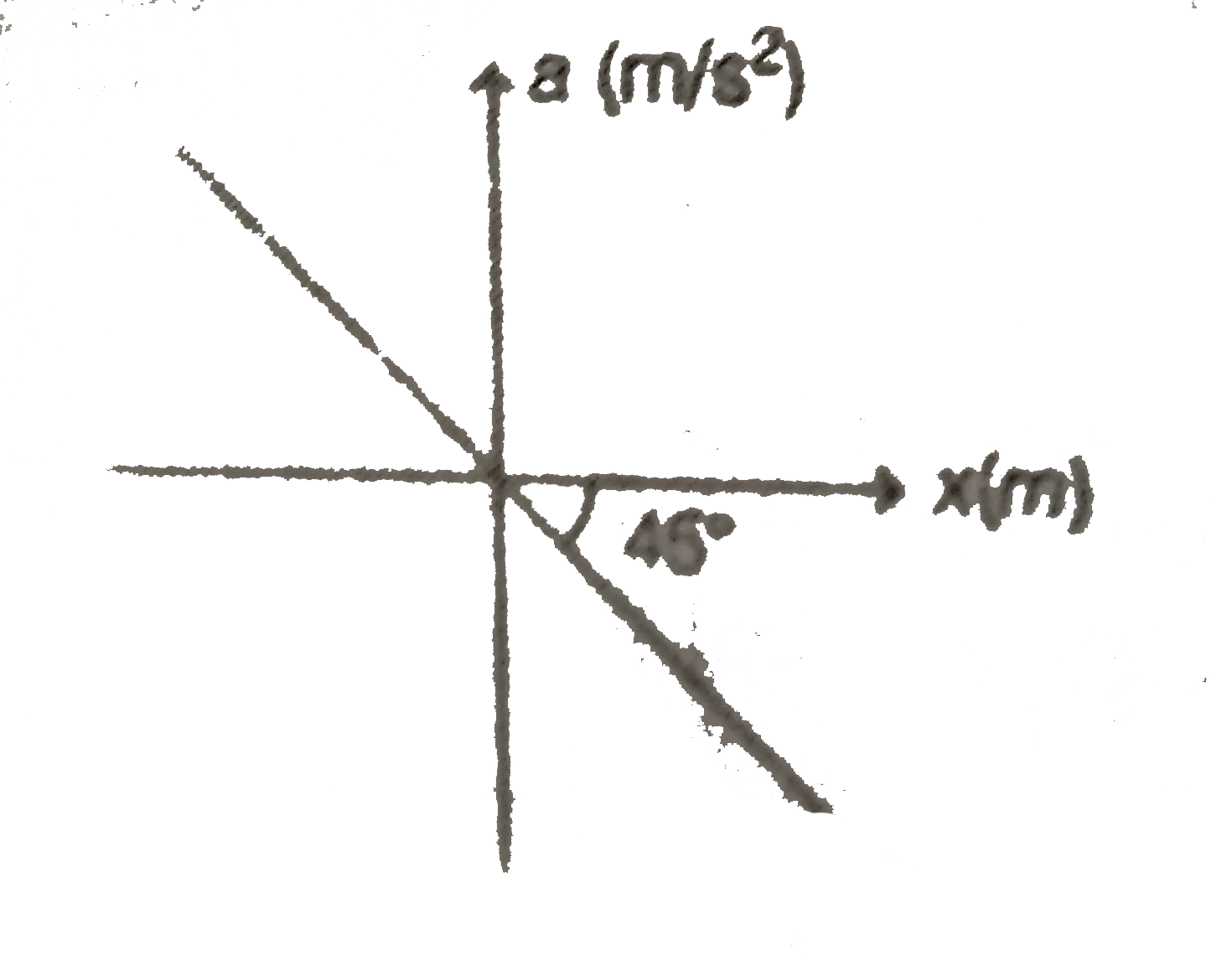
Acceleration displacement (a-x) graph of a particle executing S.H.M. is shown in the figure. The frequency of oscillation is $(tan θ = 8)$
View Solution
The displacement time graph of a particle executing S.H.M as shown in the figure.
The corresponding force-time graph of the partical will be
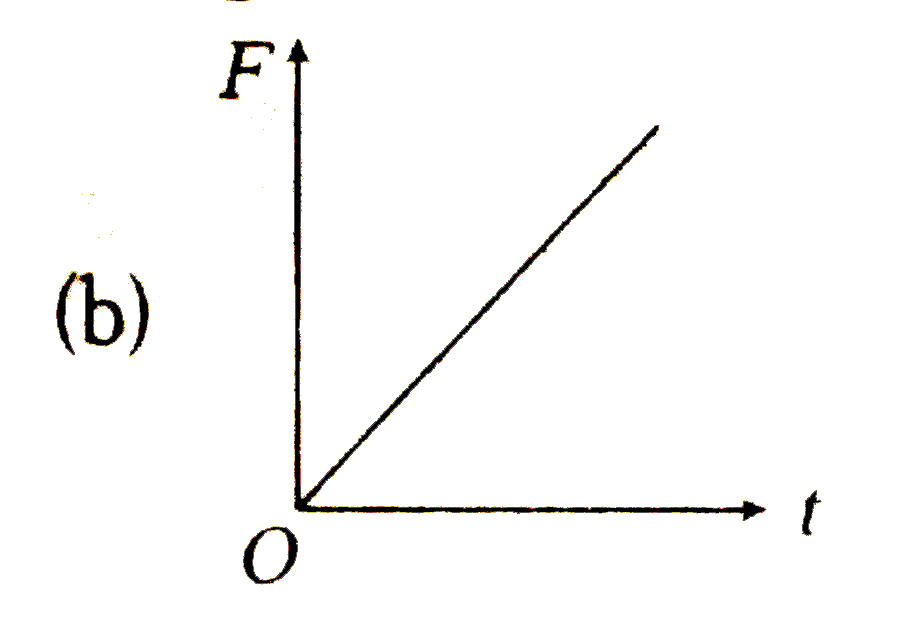
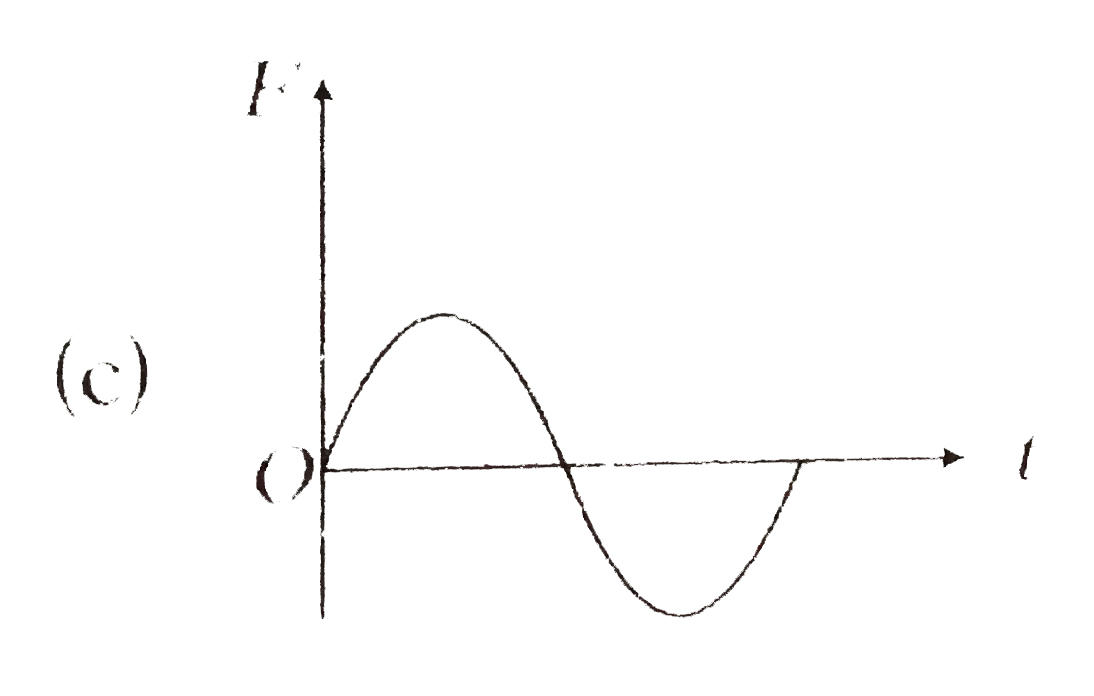
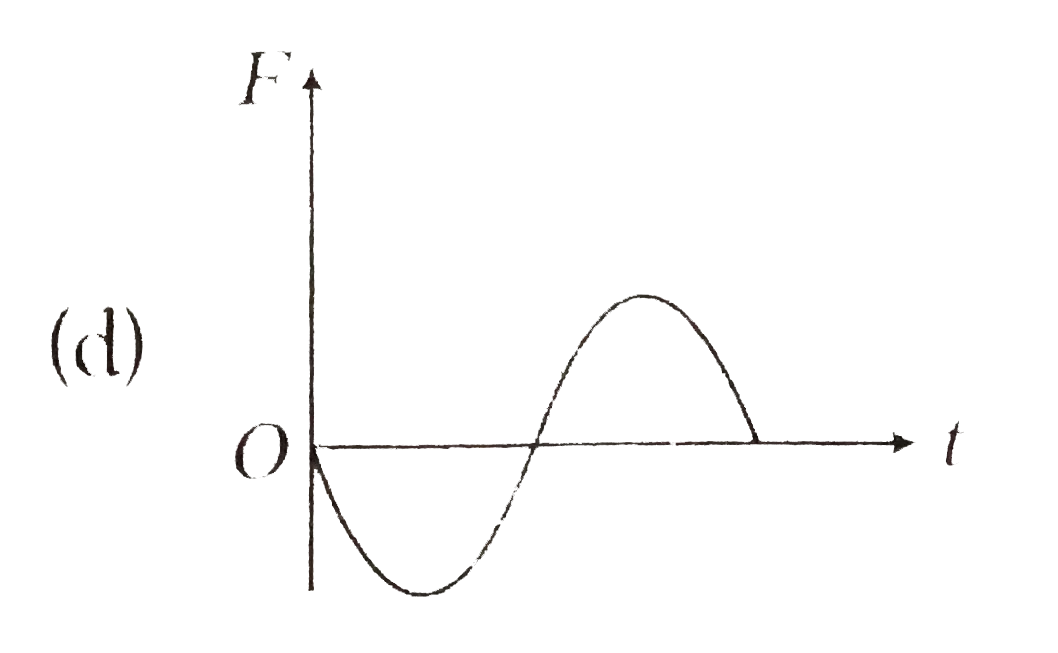
View Solution
The displacement-time graph of a particle executing SHM is as shown in the figure.

The corresponding force-time graph of the particle is
(a)

View Solution
Acceleration -displacemnet graph of a particle executing SHM is as shown in given figure. The time period of its oscillations is (in s)

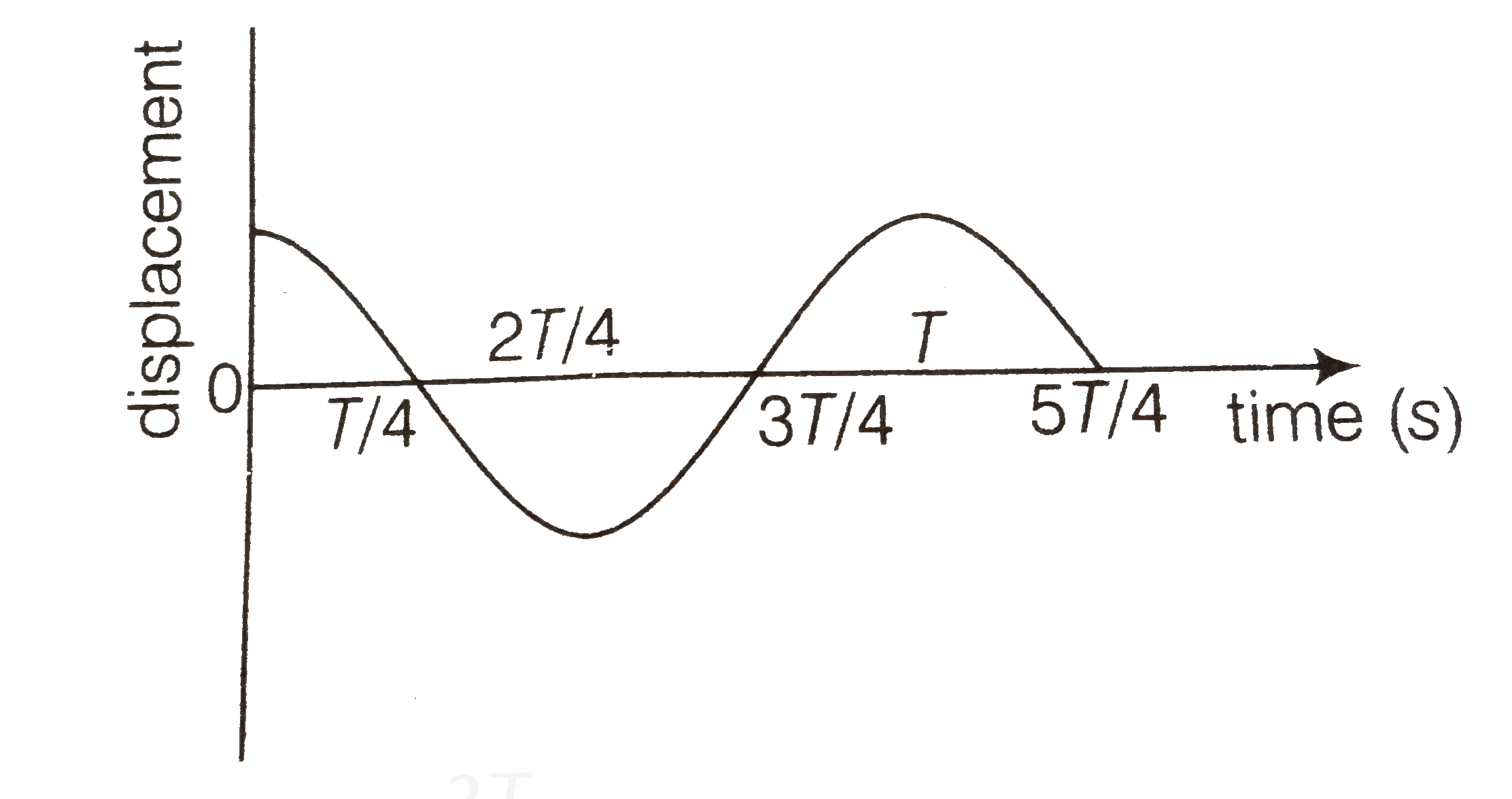
View Solution
The displacement-time graph of a particle executing SHM is shown in figure. Which of the following statement is/are true ?

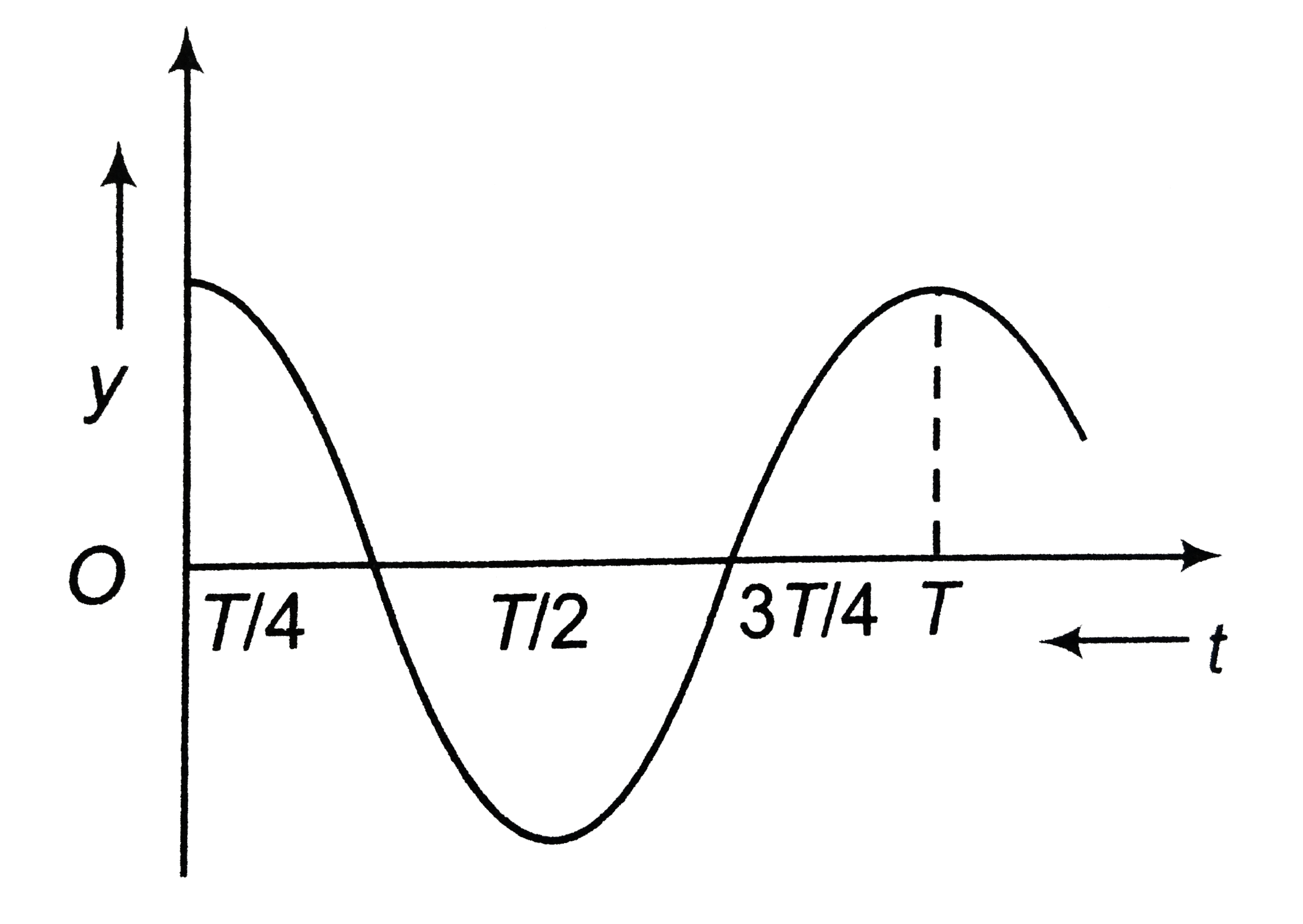
View Solution
The displacement - time graph of a particle executing SHM is shown in figure. Which of the following statements is//are true ?

View Solution
The displacement (x) is plotted with time (t) for a particle executing SHM as shown below. The correct equation of SHM is

View Solution
The displacement-time graph for a particle executing SHM is as shown in figure. Which of the following statements is correct?

View Solution
Displacement time graph of particle performing SHM is as shown in figure. Assume that mean position is at $x = 0$
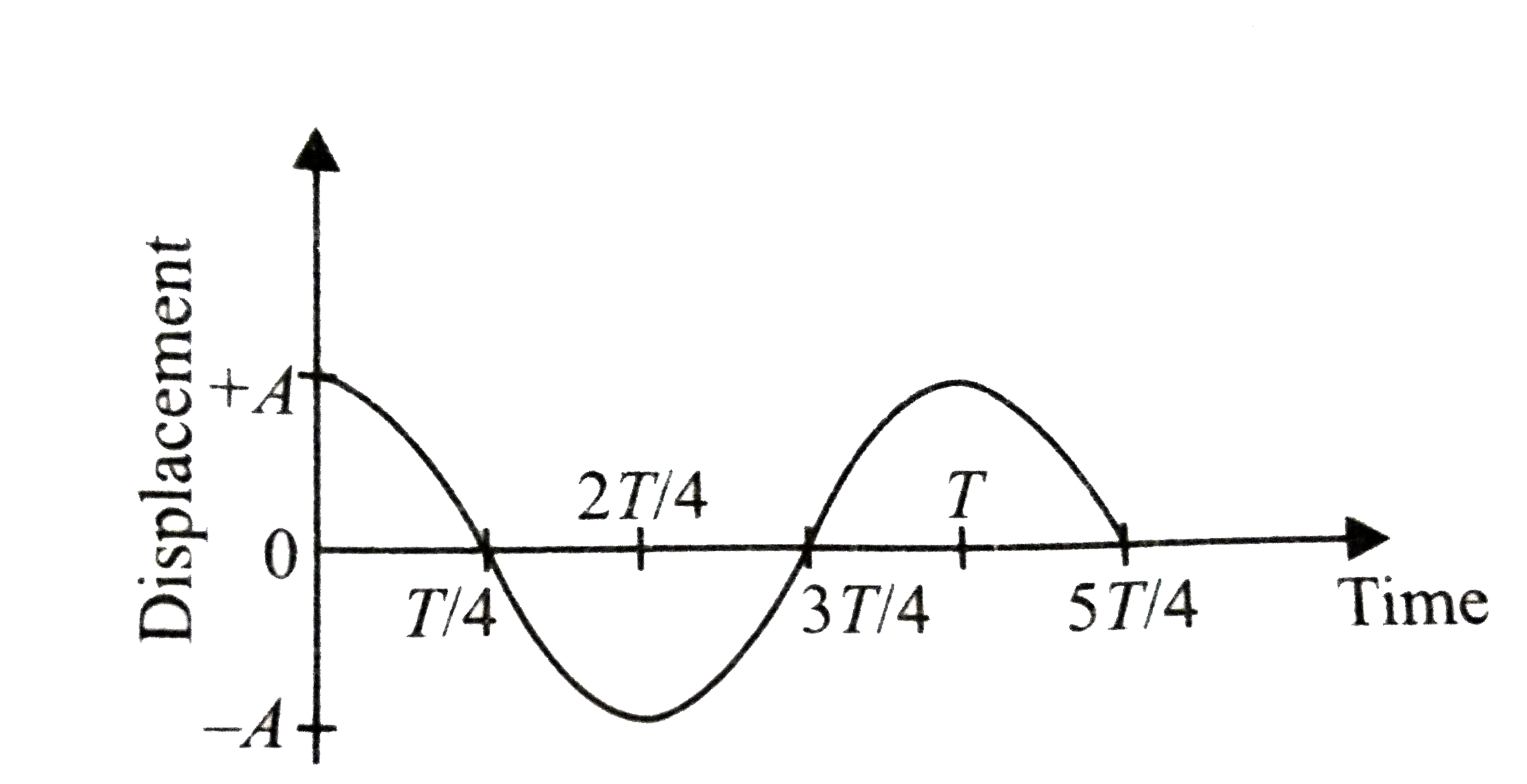
View Solution
The displacement time graph of a particle executing S.H.M. is given in figure : (sketch is schematic and not to scale).

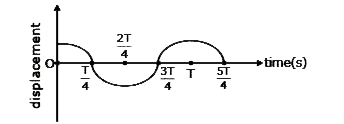
Which of the following statements is/are true for this motion?
(A) The force is zero at t = $\frac{3 T}{4}$
(B)The acceleration is maximum at t=T
(C )The speed is maximum at t = $\frac{T}{4}$
(D) The P.E. is equal to K.E. of the oscillation at t = $\frac{T}{2}$
View Solution

Displacement time(x-t) graph of a particle executing S.H.M is shown In the figure.The equation of S.H.M is given by

The correct Answer is:B

Similar Questions

Recommended Questions