Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each tract (Fig.) . Will that stones reach the bottom at the same time ? Will they reach there with the same speed ? Explain . Given nad h = 10 m, what are the speeds and times taken by the two stones ?
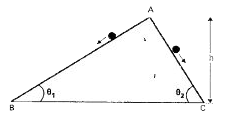
In fig OA and OB are two smooth planes inclined to the horizontal at respectively. As height of both the planes is same, therefore, both the stones, will reach the bollon with same speed.
P.E = K.E
mgh
As is clear from fig, acceleration of the two blocks are
As
From V = u + at = 0 + at (or)
As
i.e. second stone will take lesser time and reach the bottom earlier than the first stone.
Similar Questions
Two inclined frictionless tracks, one gradual and the other steep meet at O, from where two stones are allowed to slide down from rest, one on each track. Will the stones reach the bottom at the same time ? Will they reach there with the same speed ? Explain.
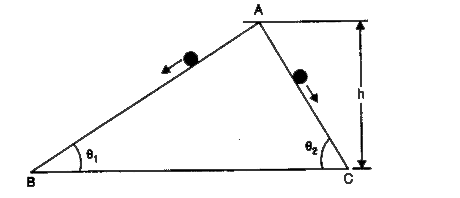
View SolutionTwo inclined frictionless tracks, one gradual and the other steep meet at A from where to stones are allowed to slide down from rest, one on each track (fig.) Will hte stones reach the bottom at the same time? Will they reach there with the same speed? Explain, given θ1=30∘, θ92)=60∘ and h=10m. What are the speeds and time taken by the two stones?
View Solution
Knowledge Check
Two inclined frictionless tracks, one gradual and the other steep meet at a from where two stones are allowed to slide down from rest, one on each track as shown in Figure. Which of the following statement is correct ?
 .ABoth the stone reach the botton at the same time but not with the same speed.BBoth the stone reach the bottom with the same speed and stone I reaches the bottom earlier than stone II Figure.CBoth the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.DBoth the stones reach the bottom at different times and with different speeds.
.ABoth the stone reach the botton at the same time but not with the same speed.BBoth the stone reach the bottom with the same speed and stone I reaches the bottom earlier than stone II Figure.CBoth the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.DBoth the stones reach the bottom at different times and with different speeds.Two inclined frictionless tracks, one gradual and the other steep meet at a from where two stones are allowed to slide down from rest, one on each track as shown in Figure. Which of the following statement is correct ?
 .ABoth the stones reach the bottom at the same time but not with the same speed.BBoth the stones reach the bottom with the same speed and stone I reaches the bottom earlier than stone II.CBoth the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.DBoth the stones reach the bottom at different times and with different speeds
.ABoth the stones reach the bottom at the same time but not with the same speed.BBoth the stones reach the bottom with the same speed and stone I reaches the bottom earlier than stone II.CBoth the stones reach the bottom with the same speed and stone II reaches the bottom earlier than stone I.DBoth the stones reach the bottom at different times and with different speedsTwo inclined frictionless tracks, one gradual and other steep meet at 'A' from where two stones are allowed to slide down from rest, one on each track as shown in figure. The speed of two stones on reaching at bottom are v1andv2 respectively. v1&v2 are related as
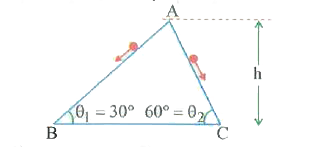 Av1>v2Bv1<v2Cv1=v2Ddata insufficient
Av1>v2Bv1<v2Cv1=v2Ddata insufficient
Two inclined frictionless tracks, one gradual and the other steep meet at A from where to stones are allowed to slide down from rest, one on each track (fig.) Will hte stones reach the bottom at the same time? Will they reach there with the same speed? Explain, given θ1=30∘, θ92)=60∘ and h=10m. What are the speeds and time taken by the two stones?

View SolutionTwo inclined frictionless tracks , one gradual and the other sleep meet at A from where two stones are allowed to slide down from rest. One on each track as shown in figure. Which of the following statement is correct?

View SolutionA stone is dropped from a height h. simultaneously, another stone is thrown up from the ground which reaches a height 4h. The two stones will cross each other after time:-
View SolutionA stone is dropped from a height h. Simultaneously, another stone is thrown up from the ground which reaches a height 4 h. The two stones cross each other after time
View SolutionA stone is dropped from a height h. simultaneously, another stone is thrown up from the ground which reaches a height 4h. The two stones will cross each other after time:-
View Solution
