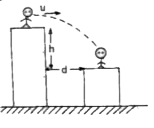
A man runs across the roof of a tall building and lumps horizontally on to the (lower) roof of an adjacent building. If his speed is 9 ms−1 and the horizontal distance between the buildings is 10 m and the height difference between the roofs is 9 m, will he be able to land on the next building ? (take g = 10 ms−2).
Difference of heights between two buildings h = 9 m, g = 10 ms−2
Time of flight of a man t=√2hg=√2×910
=1.341 spc
Horizontal speed of a man u = 9 ms−1
Horizontal distance travelled by a man dm
= Horizontal speed × Time of flight
=u×t=9×1.341=12.07m
Given, the horizontal distance between the buildings db= 10 m
Since dm>db, the man can able to land on the next building.
Similar Questions
A man runs across the roof-top of a tall building and jumps horizontally with hope of landing on the roof of the next building which is at a lower height than the first. If his speed is 9m/s,the horizontal distance between the two buildings is 10m and height difference is 9m, will he be able to land on the next building ? (take g=10m/s2).
View SolutionA man runs across the roof-top of a tall building and jumps horizontally with hope of landing on the roof fo the bext building which is at a lower height than the first. If his speed is 9m/s,the (horizontal ) destanc hetween the two buildings is 10m and height difference is 9m, will he be able to land on the bext building ? (taken g=10 m//s^(2)).
View Solution
Knowledge Check
A body is dropped from the roof of a multistoried building it passes the ceiling of the 15th storey at a speed of 20ms−1 if the height of each storey is 4m, the number of stereys in the building is (takeg=10ms−2 and neglect air resistance)
A20B25C30D35A man 2.5 m tall is 32.5 m away from a building. The angle of elevation of the top of the building from his eyes is 60∘. What is the height of the building? Also, calculate the distance between the eye of man and top point of the building.
A5879 m, 65 mB60 m, 59.5 mC58m, 60 mD59.5 m, 60,5 mFrom two points A and B on the same side of a building the angles of elevation of the top of the building are 30∘and60∘ respectively. if the height of the building is 10 m find the distances between A and B correct to two decimal places
A10 . 66 mB13 . 43 mC11 . 55 mD12 . 26 m
The angles of elevation oand depression of the top and bottom of a lighthouse from the top of a building, 60 m high, are 30∘ and 60∘ respectively. Find
(i) the difference between the heights of the lighthouse and the building.
(ii) distance between the lighthouse and the building.
View SolutionThe angle of depressions of the top and bottom of 10m tall building from the top of a multistoried building are ,30∘ and 60∘respectively,find the height of the multistoried building and the distance between the two buildings.
View SolutionThe angles of depression of the top and bottom of 12,m tall building from the top of a multistoried building are 30∘ and 45∘ respectively. Find the height of the multi storeyed building and the distance between the two buildings.
View SolutionA ball is thrown upward from the top of a 25.0 m tall building. The ball's initial speed is 12.0 m/s. At the same instant, a person is running on the ground at a distance of 31.0 m from the building. What must be the average speed of the person if he is to catch the ball at the bottom of the building ?
View SolutionA body is dropped from the roof of a multi storied building. It passes the ceiling of the 15th storey at a speed of 20ms−1. If the height of each storey is 4m, the number of storeys in the building is (takeg=10ms−2 and neglect air resistance)
View Solution
