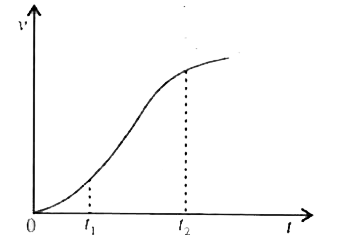
The velocity-time graph of a particle in one-dimensional motion is shown in Fig.

Which of the following formulae are correct for describing the motion of the particle over the time-interval $t_{1}$ to $t_{2}$ :
a) $x (t_{2}) = x (t_{1}) + v (t_{1}) (t_{2} - t_{1}) + (\frac{1}{2}) a {(t_{2} - t_{1})}_{2}^{2}$
b) $v (t_{2}) = v (t_{1}) + a (t_{2} - t_{1})$
c) $v_{average} = (x (t_{2}) - x (t_{1})) / (t_{2} - t_{1})$
d) $v_{average} = (v (t_{2}) - v (t_{1})) / (t_{2} - t_{1})$
e) $x (t_{2}) = x (t_{1}) + v_{average} (t_{2} - t_{1}) + (\frac{1}{2}) a_{average} {(t_{2} - t_{1})}_{2}^{2}$
f) $x (t_{2}) = x (t_{1})$ = area under the v - t curve bounded by the t-axis and the dotted line shown.

Text Solution

Verified by Experts

From the graph we note that the slope is not constant and is not uniform, hence the relations (iii), (iv), (v) are correct.

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Similar Questions

एकविमीय गति में किसी कण का वेग - समय ग्राफ चित्र में दिखाया गया है-

दिए सूत्रों में $t_{1}$ से $t_{2}$ तक के समय अंतराल की अवधि में कण की गति का वर्णन करने के लिए कौन - से सूत्र सही हैं
(i) $x (t_{2}) = x (t_{1}) + v (t_{1}) (t_{2} - t_{1}) + (1 / 2) a {(t_{2} - t_{1})}_{2}^{2}$
(i8i) $v (t_{2}) = v (t_{1}) + a (t_{2} - t_{1})$
(iii) $v_{average} = [x (t_{2}) - x (t_{1})] / (t_{2} - t_{1})$
(iv) $a_{average} = [v (t_{2}) - v (t_{1})] / (t_{2} - t_{1})$
(v) $x (t_{2}) = x (t_{1}) + v_{average} (t_{2} - t_{1}) + (1 / 2) a_{average} {(t_{2} - t_{1})}_{2}^{2}$
(vi) $x (t_{2}) - x (t_{1}) = t -$ अक्ष तथा दिखाई गई बिंदुकित रेखा के बीच दर्शाए गए वक्र के अंतर्गत आने वाला क्षेत्रफल |
View Solution
The velocity-time graph of a particle in one-dimensional motion is shown in Fig.

Which of the following formulae are correct for describing the motion of the particle over the time-interval $t_{1}$ to $t_{2}$ :
(a) $x (t_{2}) = x (t_{1}) + υ (t_{1}) (t_{2} - t_{1}) + (1 / 2) a {(t_{2} - t_{1})}_{2}^{2}$
(b) $υ (t_{2}) = υ (t_{1}) + a (t_{2} - t_{1})$
(c ) $υ_{average} = (x (t_{2}) - x (t_{1})) / (t_{2} - t_{1})$
(d) $a_{average} = (υ (t_{2}) - υ (t_{1})) / (t_{2} - t_{1})$
(e ) $x (t_{2}) = x (t_{1}) + υ_{average} (t_{2} - t_{1}) + (1 / 2) a_{average} {(t_{2} - t_{1})}_{2}^{2}$
(f) $x (t_{2}) - x (t_{1}) =$ area under the $υ - t$ curve bounded by the t-axis and the dotted line shown.
View Solution
The velocity-time graph of a particle in one-dimensional motion is shown in Fig.

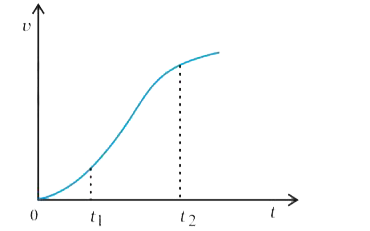
Which of the following formulae are correct for describing the motion of the particle over the time-interval $t_{1}$ to $t_{2}$ :
(a) $x (t_{2}) = x (t_{1}) + υ (t_{1}) (t_{2} - t_{1}) + (1 / 2) a {(t_{2} - t_{1})}_{2}^{2}$
(b) $υ (t_{2}) = υ (t_{1}) + a (t_{2} - t_{1})$
(c ) $υ_{average} = (x (t_{2}) - x (t_{1})) / (t_{2} - t_{1})$
(d) $a_{average} = (υ (t_{2}) - υ (t_{1})) / (t_{2} - t_{1})$
(e ) $x (t_{2}) = x (t_{1}) + υ_{average} (t_{2} - t_{1}) + (1 / 2) a_{average} {(t_{2} - t_{1})}_{2}^{2}$
(f) $x (t_{2}) - x (t_{1}) =$ area under the $υ - t$ curve bounded by the t-axis and the dotted line shown.
View Solution
Prove that the point of intersection of the tangents at $t_{1} and t_{2}$ on the parabola $y^{2} = 4 a x$ is (at1t2,a(t1+t2))
View Solution
For any arbitrary motion in space , which of the following relations are true : (a) $V_{average} = (1 / 2) (v (t_{1}) + v (t_{2}))$
(b) $V_{average} = [r (t_{2}) - r (t_{1})] / (t_{2} - t_{1})$
(c ) $V (t) = V (0) + a t$
(d) $r (t) = r (0) + v (0) T + (1 / 2) a t^{2}$
(e ) $a_{average} = [v (t_{2}) - v (t_{1})] / (t_{2} - t_{1})$
(The average stands for average of the quantity over the time interval $t_{1} to t_{2})$
View Solution
For any arbitrary motion in space , which of the following relations are true : (a) V_("average")=(1//2)(v(t_(1))+v(t_(2))) (b) V_("average")=[r(t_(2))-r(t_(1))]//(t_(2)-t_(1)) (c ) V(t)=V(0)+at (d) r(t) =r(0)+v(0)T+(1//2)at^(2) (e ) a_("average")=[v(t_(2))-v(t_(1))]//(t_(2)-t_(1)) (The average stands for average of the quantity over the time interval t_(1)" to "t_(2))
View Solution
For any arbitrary motion in space , which of the following relations are true : (a) $V_{average} = (1 / 2) (v (t_{1}) + v (t_{2}))$
(b) $V_{average} = [r (t_{2}) - r (t_{1})] / (t_{2} - t_{1})$
(c ) $V (t) = V (0) + a t$
(d) $r (t) = r (0) + v (0) T + (1 / 2) a t^{2}$
(e ) $a_{average} = [v (t_{2}) - v (t_{1})] / (t_{2} - t_{1})$
(The average stands for average of the quantity over the time interval $t_{1} to t_{2})$
View Solution
For any arbitrary motion in space , which of the following relations are true : (a) $V_{average} = (1 / 2) (v (t_{1}) + v (t_{2}))$
(b) $V_{average} = [r (t_{2}) - r (t_{1})] / (t_{2} - t_{1})$
(c ) $V (t) = V (0) + a t$
(d) $r (t) = r (0) + v (0) T + (1 / 2) a t^{2}$
(e ) $a_{average} = [v (t_{2}) - v (t_{1})] / (t_{2} - t_{1})$
(The average stands for average of the quantity over the time interval $t_{1} to t_{2})$
View Solution

From the graph we note that the slope is not constant and is not uniform, hence the relations (iii), (iv), (v) are correct.

Similar Questions

Recommended Questions