Show that a(b×c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors a, b and c.
Let a parallele piped be formed on three vectors.
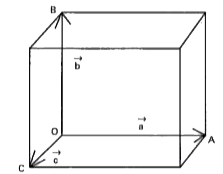
−−→OA=→a,−−→OB=→band−−→OC=→c
Now, →b×→c=bc
sin90∘ˆn=bcˆn
Where ˆn is unit vector along −−→OA perpendicular to the plne containing →band→c.
Now →a.(→b×→c)=→a.bcˆn=(a)(bc)cosO∘=abc
Which is equal in magnitude to the volume of the parallel piped.
Similar Questions
Knowledge Check
Volume of parallelepiped determined by vectors ¯a,¯b and ¯c is 5.
Then the volume of the parallelepiped determined by the vectors 3(¯a+¯b).(¯b+¯c) and 2(¯c+¯a) isA100B30C24D60If a, b, c are three non-coplanar vectors such that volume of parallelopiped formed with a ,b , c as coterminous edges is equal to volume of parallelopiped formed with a×b,b×c,c×a as coterminous edges, then :
A[abc]=0B[abc]=1C[abc]=−1D[abc]ε[−1,1]
Show that →a.(→b×→c) is equal in magnitude to the volume of the parallelopiped formed on the three vectiors, →a,→band→c.
View SolutionVolume of parallelepiped formed by vectors →a×→b,→b×→c and →c×→a is 36 then find the volume of parallelepiped formed by the vectors →a,→b and →c
View SolutionIf the volume of parallelepiped determined by vectors (2¯aׯb),(¯bׯ¯¯¯3c) and 5(¯cׯa) is equal to the volume of the parallelepiped determined by vectors 5(¯a+¯b),6(¯b+¯c) and 2(¯c+¯a), then find the volume of parallelepiped determined by vectors ¯,¯b and ¯c in cubic units.
View SolutionVolume of parallelepiped determined by vectors ¯a,¯b and ¯c is 5.
Then the volume of the parallelepiped determined by the vectors 3(¯a+¯b).(¯b+¯c) and 2(¯c+¯a) is
View SolutionVolume of parallelepiped determined by vectors →a,→band→c is 5. Then the volume of the parallelepiped determined by vectors 3(→a+→b),(→b+→c)and2(→c+→a) is
View SolutionVolume of parallelepiped formed by vectors →a×→b,→b×→cand→c×→ais36sq. units. Column I|Column II Volume of parallelepiped formed by vectors →a,→b,and→c is|p. 0sq.units Volume of tetrahedron formed by vectors →a,→b,and→c is|q. 12 sq. units Volume of parallelepiped formed by vectors →a+→b,→b+→cand→c+→a is|r. 6 sq. units Volume of parallelepiped formed by vectors →a−→b,→b−→cand→c−→a is|s. 1 sq. units
View Solution
