In deriving Bernoulli's equation, we equated the work done on the fluid in the tube to its change in the potential and kinetic energy.
a) What is the largest average velocity of blood flow in any artery of diameter 2×10−3 m if the flow must remain laminar ?
b) Do the dissipative forces become more important as the fluid velocity increases ? Discuss qualitatively.
a) If dissipative forces are present, then some forces in liquid flow due to pressure different is spent against dissipative forces. Due to which the pressure drop becomes large.
b) The dissipative forces become more important with increasing flow velocity, because of tabulence.
Similar Questions
In deriving Bernoulli's equation , we equated the workdone on the fluid in the tube to its change in the potential and kinetic energy (a) How does the pressure change as the fluid moves along the tube if dissipative forces are present ? (b) Do the dissipative forces becomes more important as the fluid velocity increase? Discuss qualitatively.
View SolutionIn deriving Bernoulli's equation , we equated the workdone on the fluid in the tube to its change in the potential and kinetic energy (a) How does the pressure change as the fluid moves along the tube if dissipative forces are present ? (b) Do the dissipative forces becomes more important as the fluid velocity increase? Discuss qualitatively.
View Solution
Knowledge Check
When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Calculate the highest average speed that blood (ρ≈1000kg/m3) could have and still remain in laminar flow when it flows through the arorta (R=8×10−3m) Take the coeffiicient of viscosity of blood to be 4×10−3Pa−sA0.5m/sB1.0m/sC1.5m/sD2.0m/s
(a) What is the largest average velocity of blood flow in an artery of radius 2×10−3m if the flow must remian laminar?
(b) What is the corresponding flow rate? Take viscosity of blood to be 2.084×10−3Pa−s. Density of blood is 1.06×103kg/m3.
View Solution(a) What is the largest average velocity of blood flow in an artery of radius 2×10−3m if the flow must remian laminar?
(b) What is the corresponding flow rate? Take viscosity of blood to be 2.084×10−3Pa−s. Density of blood is 1.06×103kg/m3.
View SolutionWhat should be the maximum average velocity of water in a tube of diameter 2 em so that the flow is laminar ? Viscosity of water is 10−3Nsm−2 ? For laminar flow R-1000.
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Calculate the highest average speed that blood (ρ≈1000kg/m3) could have and still remain in laminar flow when it flows through the arorta (R=8×10−3m) Take the coeffiicient of viscosity of blood to be 4×10−3Pa−s
View Solution(a) What is kinetic energy due to ? Derive an expression for it in case of a body of mass m moving with velocity v.
(b) If W is the work done to give a speed v to a car from rest, how much work is done to increase its speed to 2v ?
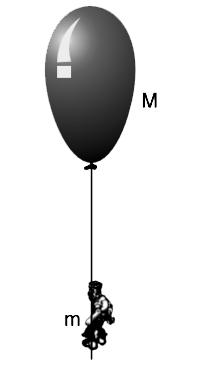
View SolutionA hot air balloon (mass M) has a passenger (mass m) and is stationary in the mid air. The passenger climbs out and slides down a rope with constant velocity u relative to the balloon.
(a) Show that when the passenger is sliding down, there is no change in mechanical energy (kinetic + gravitational potential energy) of the system (Balloon + passenger). Calculate the speed of balloon.
(b) Calculate the power of the buoyancy force on the system when the man is sliding. For easy calculation, assume that volume of man is negligible compared to the balloon.
(c) If buoyancy force is doing positive work, where is this work done lost? You have proved that sum of kinetic and potential energy of the system remains constant
View SolutionWhen the force on a object depends on the position of the object, we cannot find the work done by it on the object by simple multiplying the force by the displacement. The reason is that there is no one value for the force-it changes. So, we must find the work in tiny little displacements and then add up all the workk results. We effectively say, "Yes, the force varies over any given tiny little displacement. but the variation is so small we can approximate the force as being constant during the displacements infinitesimal, then our error becomes infinitesimal and the result becomes precise. But, to add an infinite number of work contributions by hand would take us forever, longer than a semester.So we add them up via an integration, which allows us to do all this in minutes (much less than a semester).
Force →F=(3x2N)ˆi+(4N)ˆj, with x in meters, acts on a particle, changing only the kinetic energy of th particle. How much work is done on the particle as it moves from coordinates (2 , 3 m) to 3 m, 0 m)? Does the speed of the particle increase, decrease, or remain the same?
View Solution
