If 190 MeV energy is released due to fission of each nucleus of U-235, what mass of U-235 undergoes fission per hour in a reactor of power 300 MW ?
Take 1 a.m.u. .
To solve the problem, we will follow these steps:
Step 1: Convert the energy released per fission from MeV to Joules
The energy released during the fission of each U-235 nucleus is given as 190 MeV. We need to convert this energy into Joules.
Energy (E)=190MeV×1.6×10−19J/MeV=3.04×10−11J
Step 2: Calculate the total energy produced in one hour
The power of the reactor is given as 300 MW. We need to calculate the total energy produced in one hour.
Power (P)=300MW=300×106W
Time (t)=1hour=3600seconds
Total Energy (E_total)=P×t=(300×106)×3600=1.08×1012J
Step 3: Calculate the number of fissions that occur in one hour
Now, we can find the number of U-235 nuclei that undergo fission using the total energy produced and the energy released per fission.
Number of fissions (N)=EtotalE=1.08×10123.04×10−11≈3.55×1022nuclei
Step 4: Calculate the mass of U-235 that undergoes fission
The mass of one U-235 nucleus is given as 235 amu. We need to convert this mass into kilograms and then calculate the total mass of U-235 that undergoes fission.
Mass of one nucleus=235amu=235×1.66×10−27kg≈3.901×10−25kg
Total mass (m)=N×mass of one nucleus=3.55×1022×3.901×10−25≈13.9grams
Final Answer
The mass of U-235 that undergoes fission per hour in the reactor is approximately 13.9 grams.
---
The energy released during the fission of each U-235 nucleus is given as 190 MeV. We need to convert this energy into Joules.
The power of the reactor is given as 300 MW. We need to calculate the total energy produced in one hour.
Time (t)=1hour=3600seconds
Total Energy (E_total)=P×t=(300×106)×3600=1.08×1012J
Now, we can find the number of U-235 nuclei that undergo fission using the total energy produced and the energy released per fission.
The mass of one U-235 nucleus is given as 235 amu. We need to convert this mass into kilograms and then calculate the total mass of U-235 that undergoes fission.
Total mass (m)=N×mass of one nucleus=3.55×1022×3.901×10−25≈13.9grams
The mass of U-235 that undergoes fission per hour in the reactor is approximately 13.9 grams.
Topper's Solved these Questions
- RADIOACTIVITYBOOK - ICSECHAPTER - RADIOACTIVITYEXERCISE - EXERCISE-12(A)
50 Videos
- RADIOACTIVITYBOOK - ICSECHAPTER - RADIOACTIVITYEXERCISE - MULTIPLE CHOICE TYPE
6 Videos
- QUESTION PAPER-2019BOOK - ICSECHAPTER - QUESTION PAPER-2019EXERCISE - SECTION-II
42 Videos
- REFRACTION OF LIGHTBOOK - ICSECHAPTER - REFRACTION OF LIGHTEXERCISE - DIAGRAM BASED MCQ:
5 Videos
Similar Questions
If 200 MeV energy is released in the fission of a single nucleus of .92U235, how many fissions must occur per sec to produce a power of 1 kW?
View SolutionIf 200 MeV of energy is released in the fission of one nucleus of .92U235, The number of nuclei that must undergo fission to produce energy of 1000J in 1 sec is
View Solution
Knowledge Check
If 200MeV energy is released in the fission of a single U235 nucleus, the number of fissions required per second to produce 1 kilowatt power shall be (Given 1eV=1.6×10−19J).
A3.125×1013B1.52×106C3.125×1012D3.125×1014
If 200MeV energy is released in the fission of a single U235 nucleus, the number of fissions required per second to produce 1 kilowatt power shall be (Given 1eV=1.6×10−19J).
View Solution200 Mev energy is released when one nucleus of .235U undergoes fission. Find the number of fissions per second required for producing a power of 1 mega watt.
View SolutionAn atomic power nuclear reactor can deliver 300MW. The energy released due to fission of each nucleus of uranium atom U238 is 170MeV. The number of uranium atoms fissioned per hour will be.
View SolutionIn the given arrangement the block is released from the position where the spring is unstretched. The speed of the block when it has descended through 2cm is x10. Find the value of x.
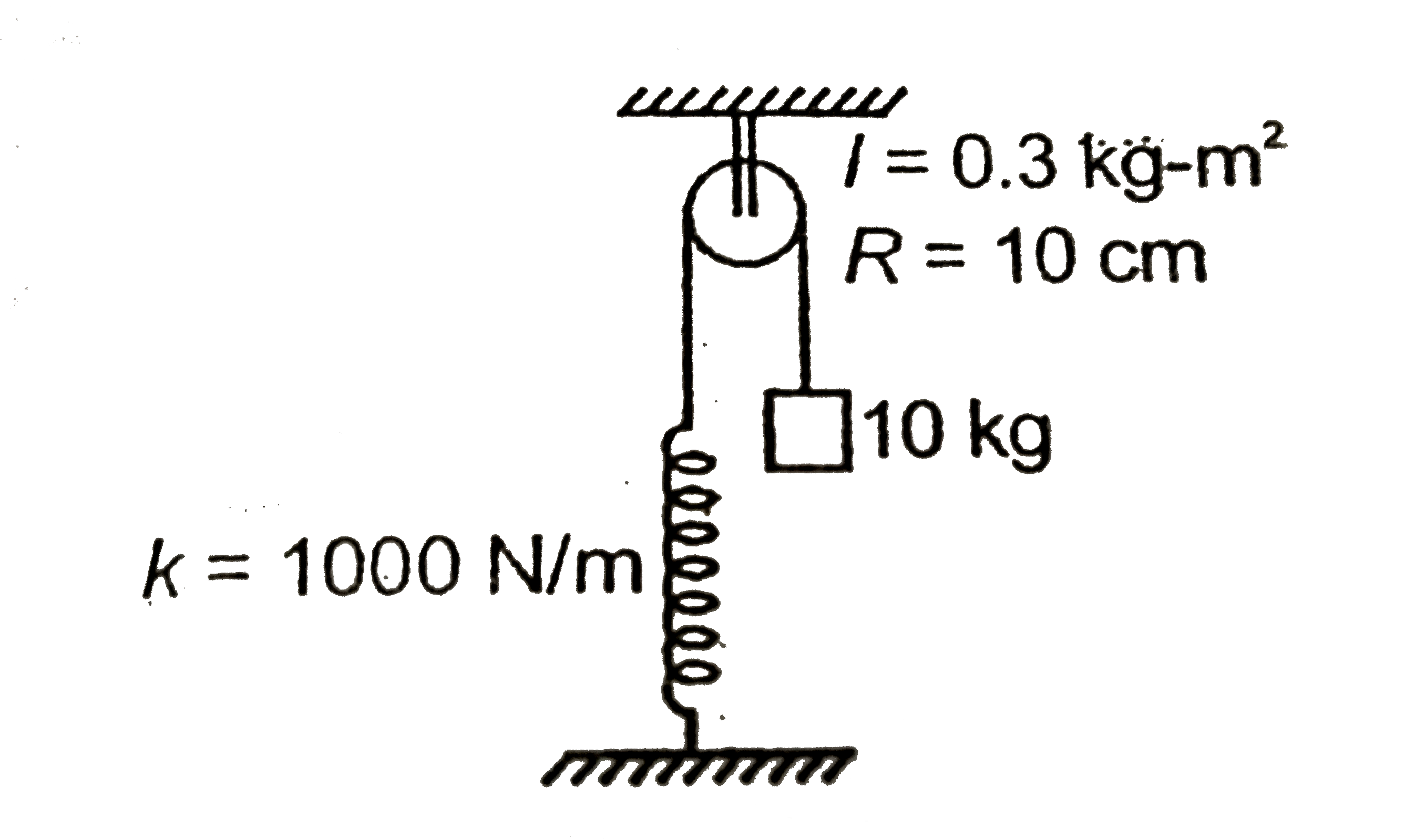
View SolutionWrite the approximate value of the energy released in the fission of one nucleus of 23592U. What is the reason for it ?
View SolutionEnergy released in the fission of a single .92U235 nucleus is 200MeV. The fission rate of a .92U235 fuelled reactor operating at a power level of 5W is.
View SolutionWhat is the energy released by fassion of 1 g of U235? (Assume 200 Me V energy is liberated on fission of 1 nucleus)
View Solution
