A half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
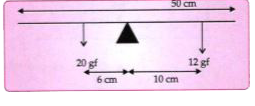
Is the rod in equilibrium ?
Since the clockwise moment (= 20 gf × 6 cm = 120 gf cm) is equal to the anticlockwise moment (= 12 gf × 10 cm = 120 gf cm), the rod is in equilibrium.
Topper's Solved these Questions
Similar Questions
A half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below:
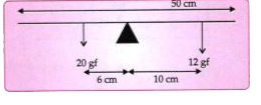
The direction of 20 kgf force is reversed. What is the magnitude of the resultant moment of the forces on the rod ?
View SolutionA half metre rod is pivoted at the centre with two weights of 20 gf and 12 gf suspended at a perpendicular distance of 6 cm and 10 cm from the pivot respectively as shown below.
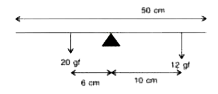
Which of the two forces acting on the rigid rod causes clockwise moment?
View Solution
Knowledge Check
Find the weight of a metre scale balanced at 30cm mark such that two weights one of 30gf and 10gf are suspended at 5cm mark and 40cm mark respectively.
A10gfB105gfC25gfD32.5gf
A very light rod of length l pivoted at O is connected with two springs of stiffness k1 & k2 at a distance of a & l from the pivot respectively. A block of mass ma attached with the spring k2 is kept on a smooth horizontal surface. Find the angular frequency of small oscillation of the block m.
_S01_031_Q01.png)
View SolutionA uniform metre rule is pivoted as its mid point. A weight of 50gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?
View SolutionA body is pivoted at a point. A force of 10N is applied at a distance of 30cm from the pivot. Calculate the moment of force about the pivot.
View SolutionA rod is pivoted about its centre. A 10 N force is applied 4 m from the pivot and another force of 5 N is applied 2 m from the pivot, as shown. The magnitude of the total torque about the pivot is

View SolutionFind the length of tangent drawn to a circle of radius 6 cm, from a point at a distance of 10 cm from the centre.
View SolutionThe diagram in Fig.1.34 shows a uniform metre rule weighing 100gf, pivoted at its centre O. Two weights 150 gf and 250 gf hang from the points A and B respectively of the metre rule such that OA= 40cm and OB=20cm . Calculate (i) the total anticlockwise moment about O, (ii) the total clockwise moment about O, (iii) the difference of anticlockwise and clockwise moments, and (iv) the distance from O where a 100gf weight should be placed to balanced the metre rule.
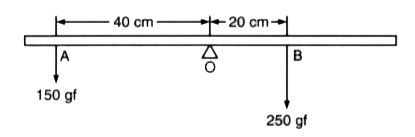
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.
View Solution
