The diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
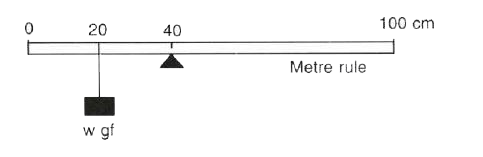
the resultant moment and its direction if the weight w is moved to the mark 30 cm.
Resultant moment =50gf×(40−10)cm−100gf×(50−40)cm
=1500gfcm−1000gfcm=500gfcm
It will rotate the metre rule anticlockwise.
Topper's Solved these Questions
Similar Questions
The diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
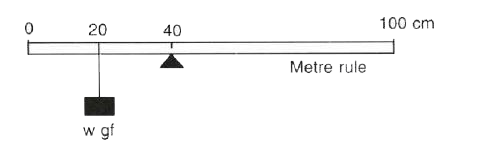
the value of w.
View SolutionThe diagram alongside shows a uniform metre rule of weight 100 gf being balanced on a knife edge placed at the 40 cm mark, by suspending a weight w gf at the mark 20 cm, find:
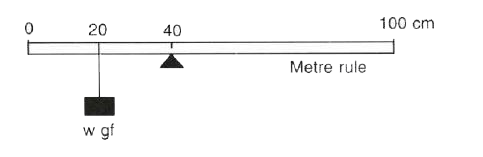
the position of another weight of 50 gf to balance the rule in part (ii).
View SolutionA uniform metre rod is balanced at the 70 cm mark by suspending a weight of 50 gf at the 40 cm mark and 200 gf at the 95 cm mark. Draw a diagram of the arrangement and calculate the weight of the metre rod.
View SolutionA uniform metre rule between horizontally on a knife edge placed at the 58cm mark when a weight of 20gf is suspended from one end.
(i) Draw a diagram of the arrangement.
(ii) What is the weight of the rule?
View SolutionA uniform metre rule of mass 100g is balanced on a fulcrum at mark 40cm by suspending an unknown mass m at the mark 20cm.
(i) Find the value of m.
(ii) To which side the rule will tilt if the mass m is moved to the mark 10cm?
(iii) What is the resultant moment now?
(iv) How can it be balanced by another mass of 50 g?
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
Draw a diagram of the arrangement.
View SolutionA uniform half metre rule balances horizontally on a knife edge at 29 cm mark when a weight of 20 gf is suspended from one end.
What is the weight of the half metre rule ?
View SolutionFigure, shows a uniform metre rule of weight W supported on a fulcrum at the 60 cm mark by applying the effort E at the 90 cm mark.

(a) State with reason whether the weight W of the rule is greater than, less than or equal to the effort E.
(b) Find the mechanical advantage in a ideal case.
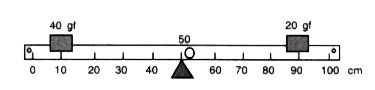
View SolutionFig.1.33 shows a uniform metre rule placed on a fulcrum at its mid point O and having a weight 40gf at the 10cm mark and a weight of 20gf at the 90cm mark. (i) Is the metre rule in equilibrium? If not , how will the turn?
(ii) How can the rule be brought in equilibrium by using an additional weight of 40 gf?
View SolutionA uniform metre rule is pivoted as its mid point. A weight of 50gf is suspended at one end of it. Where should a weight of 100gf be suspended to keep the rule horizontal?
View Solution