The separation between two masses is reduced to half. How is the magnitude of gravitational force between them affected ?
To solve the problem of how the gravitational force between two masses is affected when the separation between them is reduced to half, we can follow these steps:
1. Understand the Gravitational Force Formula:
The gravitational force F between two masses m1 and m2 separated by a distance r is given by Newton's law of gravitation:
F=Gm1m2r2
where G is the gravitational constant.
2. Initial Force Calculation:
Let’s denote the initial separation as r1. The initial gravitational force F1 can be expressed as:
F1=Gm1m2r21
3. New Separation:
According to the problem, the separation is reduced to half. Therefore, the new separation r2 is:
r2=r12
4. New Force Calculation:
Now, we need to calculate the new gravitational force F2 when the separation is r2:
F2=Gm1m2r22
Substituting r2:
F2=Gm1m2(r12)2
5. Simplifying the New Force:
Simplifying F2:
F2=Gm1m2r214=4Gm1m2r21
6. Relating New Force to Initial Force:
From the expression for F1:
F1=Gm1m2r21
We can express F2 in terms of F1:
F2=4⋅F1
7. Conclusion:
Therefore, when the separation between the two masses is reduced to half, the magnitude of the gravitational force between them becomes four times the initial gravitational force:
F2=4F1
Final Answer:
When the separation between two masses is reduced to half, the magnitude of the gravitational force between them increases to four times the initial gravitational force.
The gravitational force F between two masses m1 and m2 separated by a distance r is given by Newton's law of gravitation:
F=Gm1m2r2
where G is the gravitational constant.
Let’s denote the initial separation as r1. The initial gravitational force F1 can be expressed as:
F1=Gm1m2r21
According to the problem, the separation is reduced to half. Therefore, the new separation r2 is:
r2=r12
Now, we need to calculate the new gravitational force F2 when the separation is r2:
F2=Gm1m2r22
Substituting r2:
F2=Gm1m2(r12)2
Simplifying F2:
F2=Gm1m2r214=4Gm1m2r21
From the expression for F1:
F1=Gm1m2r21
We can express F2 in terms of F1:
F2=4⋅F1
Therefore, when the separation between the two masses is reduced to half, the magnitude of the gravitational force between them becomes four times the initial gravitational force:
F2=4F1
When the separation between two masses is reduced to half, the magnitude of the gravitational force between them increases to four times the initial gravitational force.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(A) (Multiple Choice Type)2videos
LAWS OF MOTION
- BOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - 3(B)26videos
LAWS OF MOTION
- BOOK - ICSECHAPTER - LAWS OF MOTIONEXERCISE - EXAMPLES24videos
LAWS OF MOTION
- BOOK - ICSECHAPTER - ICSE ANNUAL EXAMINATION -2020EXERCISE - SECTION-II45videos
ICSE ANNUAL EXAMINATION -2020
- BOOK - ICSECHAPTER - LIGHTEXERCISE - TOPIC 2 Spherical Mirrors (4 Marks Questions )9videos
LIGHT
Similar Questions
Knowledge Check
- Question 1 - Select One
The gravitational force between two bodies is :
Aalways repulsiveBalways attractiveCattractive only at large distancesDrepulsive only at large distances. - Question 2 - Select One
If the distance between two point particles is doubled, then the gravitational force between them
Adecreases by a factor of 4Bdecreases by a factor of 2Cincreases by a factor of 2Dincreases by a factor of 4
If the distance between two particles is reduced to half, the gravitational attraction between them will be
View SolutionIf the distance between earth and sun is doubled, they by what factor will the gravitational force between them be changed ?
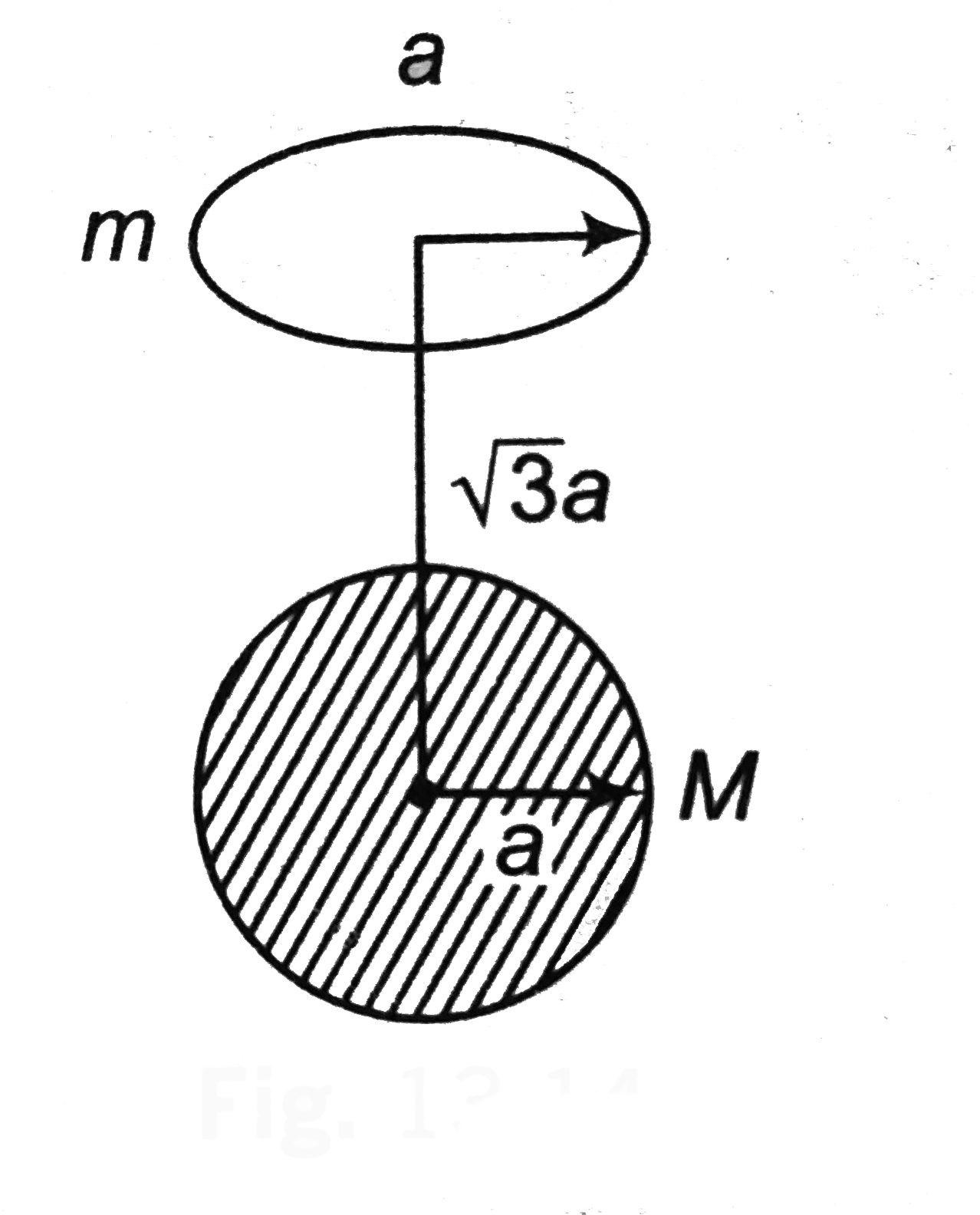
View SolutionA uniform ring of mass m is lying at a distance √3 a from the centre of mass M just over the sphere (where a is the radius of the ring as well as that of the sphere). Find the magnitude of gravitational force between them .
 View Solution
View SolutionHow does the distance of separation between two bodies affect the magnitude of the non-contact force between them ?
View SolutionIf the masses of two bodies are quadrupled and the distance between their centers is doubled, then how many times the force of gravitation between them will be changed ?
View SolutionIf the masses of two bodies are quadrupled and the distance between their centres is doubled, then how many times the force of gravitation between them will be changed ?
View Solution

