ABCD is a square with each side 12 cm. P is a point on BC such that area of ΔABP : area of trapezium APCD = 1:5. Find the length of CP.
The correct Answer is:8 cm
To solve the problem, we need to find the length of CP given that ABCD is a square with each side measuring 12 cm, and the ratio of the area of triangle ABP to the area of trapezium APCD is 1:5.
1. Understand the Geometry:
- We have a square ABCD with vertices A(0, 12), B(0, 0), C(12, 0), and D(12, 12).
- Point P is on side BC, which means its coordinates can be expressed as P(0, y) where 0 ≤ y ≤ 12.
2. Identify Areas:
- The area of triangle ABP can be calculated using the formula for the area of a triangle:
Area=12×base×height
- Here, the base AB is 12 cm (the height from A to line BP is the y-coordinate of P).
3. Calculate Area of Triangle ABP:
- The base AB = 12 cm and height = y (the y-coordinate of point P).
- Thus, the area of triangle ABP is:
AreaABP=12×12×y=6y
4. Calculate Area of Square ABCD:
- The area of square ABCD is:
AreaABCD=12×12=144 cm2
5. Calculate Area of Trapezium APCD:
- The area of trapezium APCD can be found by subtracting the area of triangle ABP from the area of square ABCD:
AreaAPCD=AreaABCD−AreaABP=144−6y
6. Set Up the Ratio:
- According to the problem, the ratio of the area of triangle ABP to the area of trapezium APCD is 1:5:
6y144−6y=15
7. Cross Multiply to Solve for y:
- Cross multiplying gives:
5×6y=1×(144−6y)
- This simplifies to:
30y=144−6y
- Adding 6y to both sides results in:
36y=144
- Dividing both sides by 36 gives:
y=4
8. Find Length of CP:
- Since P is on BC, and BC is vertical, the length CP is the distance from C(12, 0) to P(0, 4).
- The length CP can be calculated as:
CP=12−y=12−4=8 cm
Final Answer:
The length of CP is 8 cm.
- We have a square ABCD with vertices A(0, 12), B(0, 0), C(12, 0), and D(12, 12).
- Point P is on side BC, which means its coordinates can be expressed as P(0, y) where 0 ≤ y ≤ 12.
- The area of triangle ABP can be calculated using the formula for the area of a triangle:
Area=12×base×height
- Here, the base AB is 12 cm (the height from A to line BP is the y-coordinate of P).
- The base AB = 12 cm and height = y (the y-coordinate of point P).
- Thus, the area of triangle ABP is:
AreaABP=12×12×y=6y
- The area of square ABCD is:
AreaABCD=12×12=144 cm2
- The area of trapezium APCD can be found by subtracting the area of triangle ABP from the area of square ABCD:
AreaAPCD=AreaABCD−AreaABP=144−6y
- According to the problem, the ratio of the area of triangle ABP to the area of trapezium APCD is 1:5:
6y144−6y=15
- Cross multiplying gives:
5×6y=1×(144−6y)
- This simplifies to:
30y=144−6y
- Adding 6y to both sides results in:
36y=144
- Dividing both sides by 36 gives:
y=4
- Since P is on BC, and BC is vertical, the length CP is the distance from C(12, 0) to P(0, 4).
- The length CP can be calculated as:
CP=12−y=12−4=8 cm
The length of CP is 8 cm.
Topper's Solved these Questions
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(C)
27 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(A)
18 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
Similar Questions
Each side of a square ABCD is 12 cm A point P l lies on side DC such that area of ΔADP : area of trapezium ABCP = 2 : 3 Find DP .
View SolutionIn the given figure, ABCD is a square of side 7 cm. DPBA and DQBC are quardrants of circles each of the radius 7 cm. Find the area of the shaded region.

View Solution
Knowledge Check
The lengths of parallel sides of a trapezium are in the ratio 3:5 and the distance between them is 10cm. If the area of the trapezium is 120cm2, find the lengths of its parallel sides.
A9cm and 17cmB8cm and 15cmC9cm and 15cmD5cm and 17cm
Find the area of a square whose side is 5cm.
View SolutionIn the given figure, ABCD is a square of side 21 cm. AC and BD are two diagonals of the square. Two semi circles are drawn with AD and BC as diameters. Find the area of the shaded region
(Take π=227)
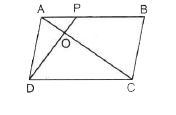
View SolutionThe given figure shows a parallelogram ABCD with area 324sq. cm. P is a point in AB such that AP:PB= 1:2. Find the area of ΔAPD.
View SolutionIn Figure-5, ABCD is a square with side 7 cm. A circle in drawn [circumscribing the square. Find the area of the shaded region.
View SolutionIn Figure ABCD is a square with side 7 cm. A circle is drawn circumscribing the square . Find the area of the shaded region .

View SolutionA square has the same area as that of a rectangle. The length and the breadth of the rectangle are 9cm and 4cm, respectively.
Find the length of a side of the square.
View SolutionIn Figure - 5, ABCD is a square with side 7 cm A circle is drawn circumscribing the square. Find the area of the shaded region.

View Solution
