In a triangle ABC, right-angled at B, side BC = 20 cm and angle A= 30°. Find the length of AB.
The correct Answer is: cm
To solve the problem step-by-step, we will use the properties of right triangles and trigonometric ratios.
Step 1: Understand the Triangle
We have a right triangle ABC, where:
- Angle B is the right angle (90°).
- Angle A is given as 30°.
- Side BC (the side opposite to angle A) is given as 20 cm.
Step 2: Find Angle C
Using the property that the sum of angles in a triangle is 180°, we can find angle C:
Angle C=180°−Angle A−Angle B=180°−30°−90°=60°
Step 3: Identify the Sides
In triangle ABC:
- AB is the side we want to find (let's denote it as x).
- BC is the side opposite angle A, which is 20 cm.
- AC is the hypotenuse of the triangle.
Step 4: Use the Tangent Function
Since we know angle A (30°) and the opposite side (BC), we can use the tangent function:
tan(A)=OppositeAdjacent=BCAB
This can be rewritten as:
tan(30°)=20x
Step 5: Substitute the Value of Tangent
We know that:
tan(30°)=1√3(or approximately 0.577)
So we can substitute this into the equation:
1√3=20x
Step 6: Cross Multiply to Solve for x
Cross multiplying gives us:
x=20√3
Step 7: Calculate the Approximate Value
To find the numerical value, we can use the approximate value of √3≈1.732:
x≈20×1.732=34.64 cm
Final Answer
The length of AB is 20√3 cm or approximately 34.64 cm.
---
We have a right triangle ABC, where:
- Angle B is the right angle (90°).
- Angle A is given as 30°.
- Side BC (the side opposite to angle A) is given as 20 cm.
Using the property that the sum of angles in a triangle is 180°, we can find angle C:
Angle C=180°−Angle A−Angle B=180°−30°−90°=60°
In triangle ABC:
- AB is the side we want to find (let's denote it as x).
- BC is the side opposite angle A, which is 20 cm.
- AC is the hypotenuse of the triangle.
Since we know angle A (30°) and the opposite side (BC), we can use the tangent function:
tan(A)=OppositeAdjacent=BCAB
This can be rewritten as:
tan(30°)=20x
We know that:
tan(30°)=1√3(or approximately 0.577)
So we can substitute this into the equation:
1√3=20x
Cross multiplying gives us:
x=20√3
To find the numerical value, we can use the approximate value of √3≈1.732:
x≈20×1.732=34.64 cm
The length of AB is 20√3 cm or approximately 34.64 cm.
Topper's Solved these Questions
Similar Questions
ΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionThe given figure shows an equilateral triangle ABC whose side is 10 cm and a right-angled BDC inside it, whose side BD = 8 cm and ∠D=90∘. Find the area of the shaded portion.
 View Solution
View SolutionIn a right triangle ABC, right angled at C, if a = 7 cm and b = 7√3 cm, then ∠A=
View SolutionConstruct a right-angled triangle ABC, right-angled at A, with hypotenuse BC = 10 cm long and one of the sides AB = 6 cm long. Also, find the midpoint D of the hypotenuse. Join AD and measure AD.
View SolutionConstruct a right-angled triangle ABC, right-angled at A, with hypotenuse BC = 7.5 cm and one of the sides AB = 5.5 cm. Also, from the point A, drop a perpendicular on BC, intersecting BC at D. Find AB : AD.
View SolutionIn triangle ABC, ∠B=90∘ and tan A = 0.75 If AC = 30 cm, find the lengths of AB and BC.
View SolutionThe given figure shows an equilateral triangle ABC whose each side is 10 cm and a right-angled triangle BDC whose side BD = 8 cm and ∠D=90∘. Find the area of the shaded portion.
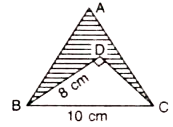 View Solution
View SolutionConstruct a right-angled triangle ABC, right-angled at A, with hypotenuse BC = 6.3 cm long and one of the sides AB = 4.8 cm long. Also, find the mid-point D of the hypotenuse. Join AD and measure AD.
View SolutionIn triangle ABC,AB=6,AC=3√6,∠B=60∘ and ∠C=45∘. Find length of side BC.
View SolutionIn trapezium ABCD, as shown, AB // DC, AD = DC = BC = 20 cm and ∠A=60∘. Find:
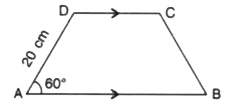
(i) length of ABView Solution

