A line through origin meets the line x=3y+2 at right angles at point X. Find the co-ordinates of X.
The correct Answer is:(15,−35)
To solve the problem step by step, we will find the coordinates of the point X where the line through the origin meets the line x=3y+2 at right angles.
Step 1: Identify the equations of the lines
The line through the origin can be represented as:
y=mx
where m is the slope of the line.
The given line is:
x=3y+2
Step 2: Convert the given line to slope-intercept form
To find the slope of the given line, we need to rearrange it into the form y=mx+c. Starting from:
x=3y+2
we can rearrange it as follows:
3y=x−2
y=13x−23
From this, we can see that the slope m1 of the line x=3y+2 is:
m1=13
Step 3: Determine the slope of the line through the origin
Since the two lines are perpendicular, the product of their slopes must equal -1. Let the slope of the line through the origin be m:
m⋅m1=−1
m⋅13=−1
Solving for m:
m=−3
Step 4: Write the equation of the line through the origin
Now that we have the slope, the equation of the line through the origin is:
y=−3x
Step 5: Solve the two equations simultaneously
We need to find the point of intersection of the lines y=−3x and y=13x−23. We can set them equal to each other:
−3x=13x−23
Step 6: Clear the fractions
To eliminate the fraction, multiply the entire equation by 3:
−9x=x−2
Step 7: Rearrange the equation
Rearranging gives:
−9x−x=−2
−10x=−2
Dividing by -10:
x=15
Step 8: Find the y-coordinate
Now substitute x=15 back into the equation of the line through the origin to find y:
y=−3(15)=−35
Step 9: Write the coordinates of point X
Thus, the coordinates of point X where the two lines meet at right angles are:
(15,−35)
Summary of the solution
The coordinates of point X are:
(15,−35)
The line through the origin can be represented as:
y=mx
where m is the slope of the line.
x=3y+2
To find the slope of the given line, we need to rearrange it into the form y=mx+c. Starting from:
x=3y+2
we can rearrange it as follows:
3y=x−2
y=13x−23
m1=13
Since the two lines are perpendicular, the product of their slopes must equal -1. Let the slope of the line through the origin be m:
m⋅m1=−1
m⋅13=−1
Solving for m:
m=−3
Now that we have the slope, the equation of the line through the origin is:
y=−3x
We need to find the point of intersection of the lines y=−3x and y=13x−23. We can set them equal to each other:
−3x=13x−23
To eliminate the fraction, multiply the entire equation by 3:
−9x=x−2
Rearranging gives:
−9x−x=−2
−10x=−2
Dividing by -10:
x=15
Now substitute x=15 back into the equation of the line through the origin to find y:
y=−3(15)=−35
Thus, the coordinates of point X where the two lines meet at right angles are:
(15,−35)
The coordinates of point X are:
(15,−35)
Topper's Solved these Questions
- EQUATION OF A LINEBOOK - ICSECHAPTER - EQUATION OF A LINEEXERCISE - EXERCISE 14(D)
41 Videos
- CYLINDER, CONE AND SPHERE BOOK - ICSECHAPTER - CYLINDER, CONE AND SPHERE EXERCISE - EXERCISE 20 (G)
23 Videos
- FACTORISATIONBOOK - ICSECHAPTER - FACTORISATIONEXERCISE - M.C.Q(Competency Based Questions )
15 Videos
Similar Questions
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
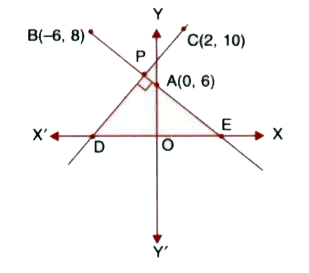
co-ordinates of points E and D.
View SolutionA line through the point (3, 0) meets the variable line y=tx at right angle at the point P. Find, in terms of t, the co-ordinates of P.
Find the value of k for which Plies on the curve x2+y2=kx.
View SolutionA point P (-2, 3) is reflected in line x = 2 to point P'. Find the co-ordinates of P'.
View SolutionIn the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
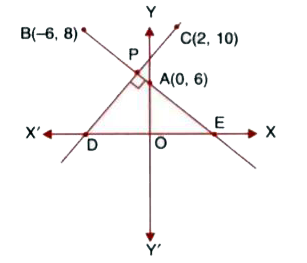
equation of line AB.
View SolutionIn the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find :
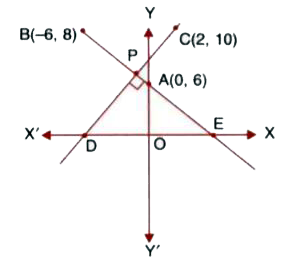
equation of line CD.
View SolutionThe perpendicular from the origin to the line y=mx+cmeets it at the point (1,2). Find the values of m and c.
View SolutionIf a line passes through the points (a,1) and (3,−5), meets the line 3x+y−1=0 at right angle, then find the value of 'a'.
View SolutionThe line 3x - 4y + 12 = 0 meets x-axis at point A and y-axis at point B. Find :
the co-ordinates of A and B.
View SolutionThe equation of a line is 3x−4y+12=0. It meets the x-axis at point A and the y-axis at point B. Find :
the co-ordinates of points A and B.
View SolutionThe line through the points (h, 3) and (4, 1) intersects the line 7x−9y−19=0at right angle. Find the value of h.
View Solution
