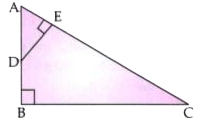
ABC is a right angled triangle with . D is any point on AB and DE is perpendicular to AC. Prove that:

.
Step by step video & image solution for ABC is a right angled triangle with ABC = 90^@. D is any point on AB and DE is perpendicular to AC. Prove that: DeltaADE~DeltaACB. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(D)
18 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
ABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC. Prove that :

(i) ΔADE~ΔACB.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

Find, area of AADE: area of quadrilateral BCED.
View SolutionABC is a right angled triangle with ABC=90∘. D is any point on AB and DE is perpendicular to AC. Prove that:

If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC. Prove that :
(iii) Find area of Δ ADE : area of quadrilateral BCED.If AC = 13 cm, BC = 5 cm and AE = 4 cm.
View SolutionABC is a right angled triangle with ∠ABC=90∘, D is any point on AB and DE is perpendicular to AC.
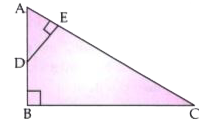
(ii) If AC = 13 cm, BC = 5 cm and AE = 4 cm. Find DE and AD.
View SolutionABC is a right triangle right-angled at B. Let D and E be any points on AB and BC respectively. Prove that AE2+CD2=AC2+DE2
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that
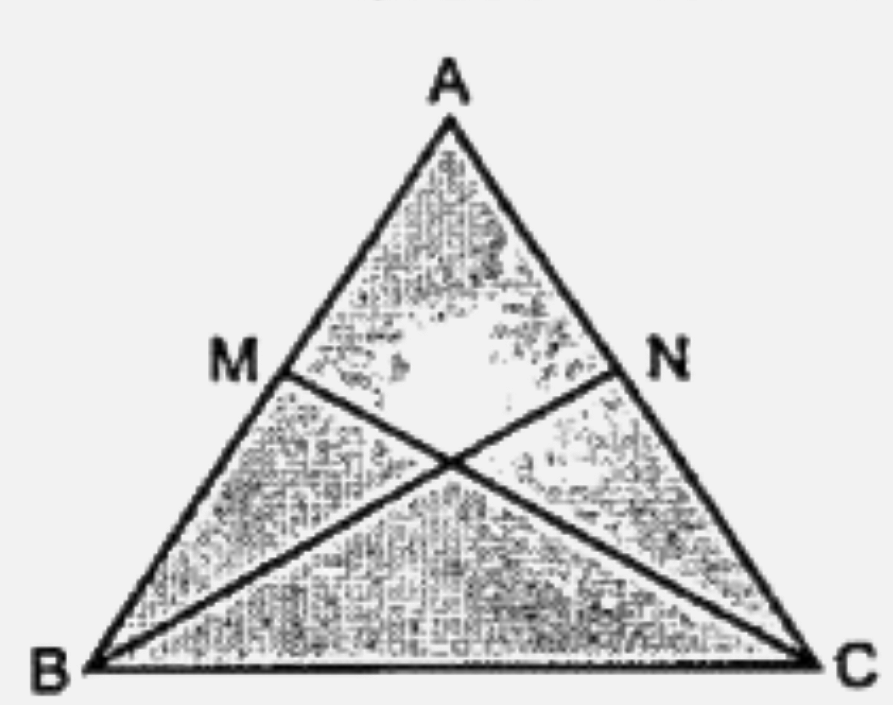
ΔAMC≅ΔANB
View SolutionThe following figure shows a triangle ABC in which AB=AC. M is a point on AB and N is a point on AC such that BM = CN. Prove that

ΔBMC≅ΔCNB
View SolutionIn triangle ABC, AB=AC and BD is perpendicular to AC. Prove that : BD2−CD2=2CD×AD
View SolutionABC is a triangle, right angled at B. If BCDE is a square on side BC and ACFG is a square on AC, prove that AD = BF.
View Solution
