The radius of a circle is given as 15 cm and chord AB subtends an angle of 131∘ at the centre C of the circle . Using trigonometry. calculate :
the length of AB,
The correct Answer is:27 . 3 m
To find the length of chord AB in a circle with a radius of 15 cm that subtends an angle of 131 degrees at the center, we can follow these steps:
Step 1: Understand the Geometry
- Draw a circle with center C and radius 15 cm.
- Mark points A and B on the circumference such that chord AB subtends an angle of 131 degrees at the center C.
Step 2: Identify Key Points
- Since CA and CB are both radii of the circle, we have:
- CA = 15 cm
- CB = 15 cm
- The angle ∠ACB = 131 degrees.
Step 3: Bisect the Angle
- Draw a perpendicular line from point C to chord AB, meeting it at point P. This line bisects chord AB into two equal segments, AP and PB.
- Therefore, AP = PB = AB/2.
- The angle ∠APC = ∠BPC = 131/2 = 65.5 degrees.
Step 4: Use Trigonometry
- In triangle ACP, we can use the sine function:
sin(65.5∘)=APAC
where AC is the radius (15 cm).
Step 5: Solve for AP
- Rearranging the equation gives:
AP=AC⋅sin(65.5∘)
Substituting the values:
AP=15⋅sin(65.5∘)
- Using the value of sin(65.5∘)≈0.91:
AP=15⋅0.91≈13.65 cm
Step 6: Find the Length of AB
- Since AP is half of AB:
AB=2⋅AP=2⋅13.65≈27.30 cm
Final Answer
The length of chord AB is approximately 27.30 cm.
---
- Draw a circle with center C and radius 15 cm.
- Mark points A and B on the circumference such that chord AB subtends an angle of 131 degrees at the center C.
- Since CA and CB are both radii of the circle, we have:
- CA = 15 cm
- CB = 15 cm
- The angle ∠ACB = 131 degrees.
- Draw a perpendicular line from point C to chord AB, meeting it at point P. This line bisects chord AB into two equal segments, AP and PB.
- Therefore, AP = PB = AB/2.
- The angle ∠APC = ∠BPC = 131/2 = 65.5 degrees.
- In triangle ACP, we can use the sine function:
sin(65.5∘)=APAC
where AC is the radius (15 cm).
- Rearranging the equation gives:
AP=AC⋅sin(65.5∘)
Substituting the values:
AP=15⋅sin(65.5∘)
- Using the value of sin(65.5∘)≈0.91:
AP=15⋅0.91≈13.65 cm
- Since AP is half of AB:
AB=2⋅AP=2⋅13.65≈27.30 cm
The length of chord AB is approximately 27.30 cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - HEIGHTS AND DISTANCES EXERCISE - Exercise 22 B19videos
HEIGHTS AND DISTANCES
- BOOK - ICSECHAPTER - GST [GOODS AND SERVICES TAX] EXERCISE - Exercise 1(B)16videos
GST [GOODS AND SERVICES TAX]
- BOOK - ICSECHAPTER - LINEAR INEQUATIONSEXERCISE - Competency Based Questions15videos
LINEAR INEQUATIONS
Similar Questions
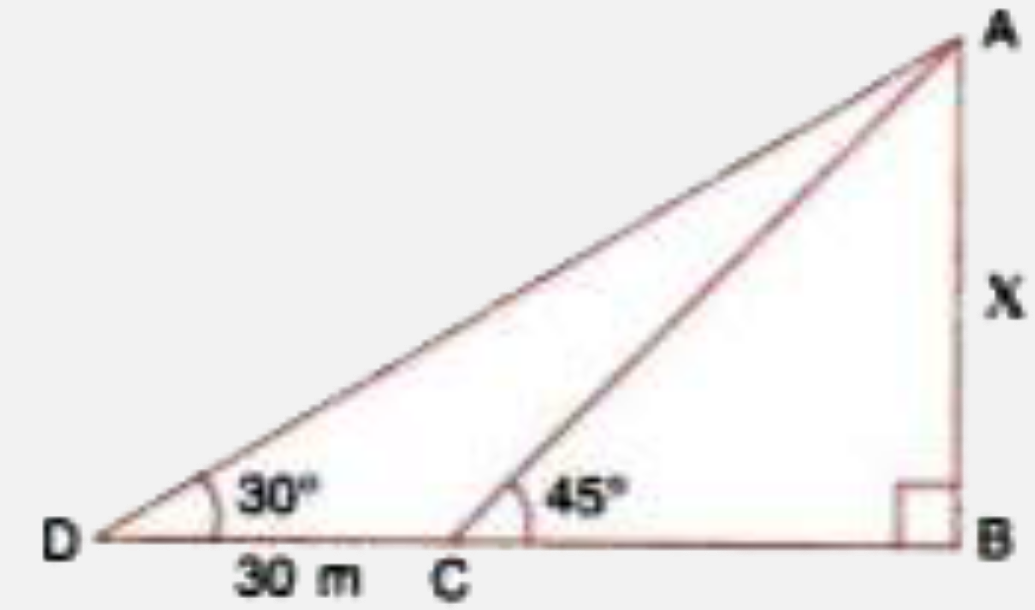
In the figure, given below, it is given that AB is perpendicular ot BD and is of length X metres. DC = 30 m, ∠ADB=30∘and∠ACB=45∘. Without using tables, find X
 03:08View Solution
03:08View SolutionFill in the blanks :
When the goods/services are sold for Rs. 15,000 under intra-state transaction from station A to station B and the rate of GST is 12%,
As per GST system
(a) S.P. at station A = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(b) CGST = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
SGST = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(c ) C.P. at station B = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(d) If profit = Rs. 5,000
S.P. at station B = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Now the same goods/services are moved under inter-state transaction from station B to station and the rate of tax is 12%.
(e ) GST = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(f) C.P. at station C = . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .02:13View SolutionTwo real numbers or two algebraic expressions related by the symbols >,<,≤or≥ form an inequation. If the highest power of the variables used in the inequation is 1, then the inequation is called linear inequation. For the linear inequation 3x−5≤8, answer teh following questions.
If x∈I, then the highest value of x is02:45View SolutionIn the given figure,chord AB subtends an angle of 115^(@) at the centre O of a circle of radius 20cm. Calculate AB correct to nearest cm.
01:22View SolutionIn a circle , chord AB subtends an angle of 60∘ at the centre and chord CD subtends 120∘, at it. Then which chord is longer ?
02:38View SolutionThe radius of a circle is 8 cm and O is its centre. If ∠AOB=60∘ and AB is a chord, then what is the length of the chord AB?
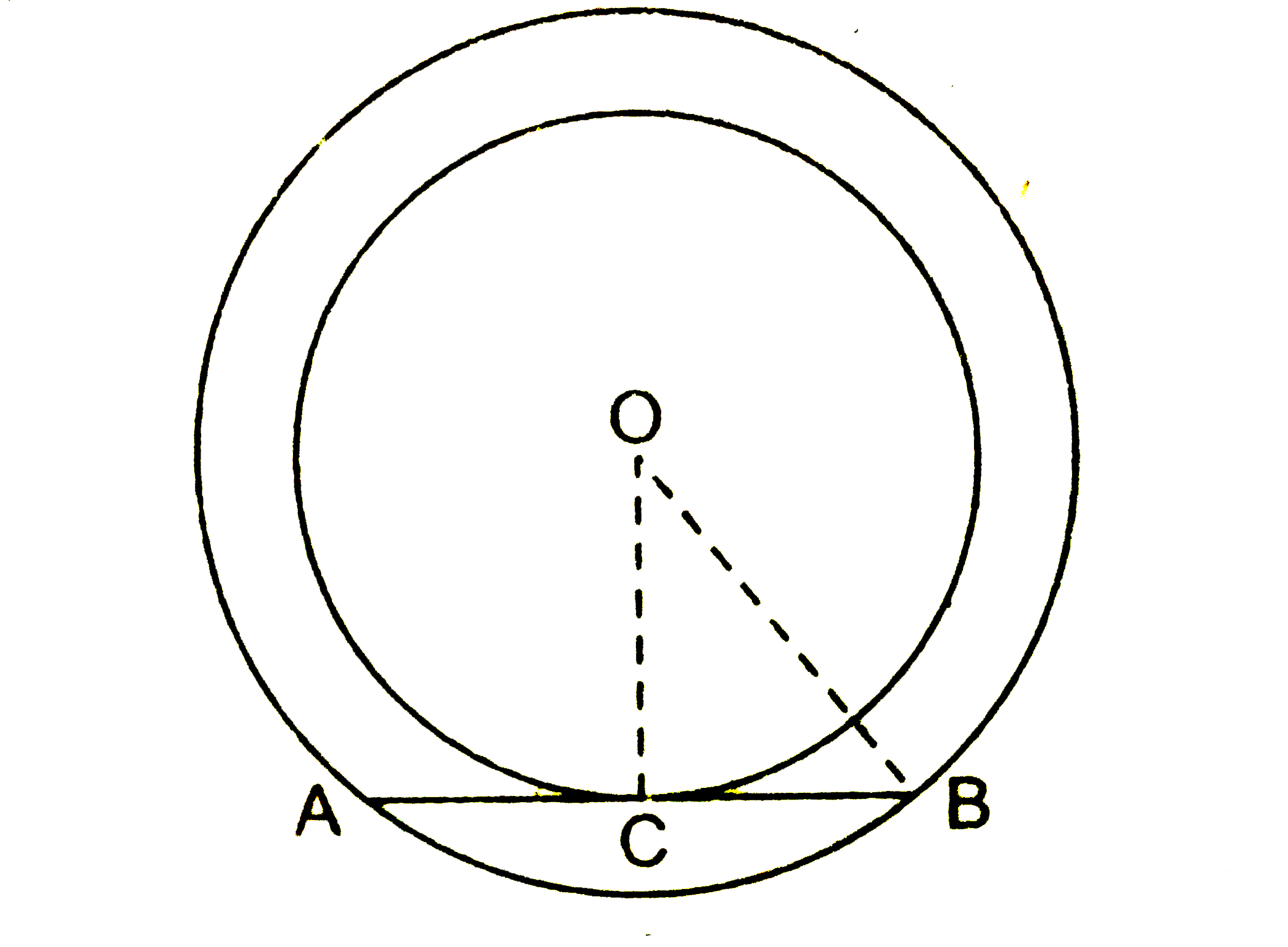
04:46View Solution15 सेमी और 17 सेमी त्रिज्या के दो समकेन्द्रीय वृत्त हैं। यदि बड़े वृत की जीवा AB अन्दर वाले वृत्त हैं। यदि बड़े वृत्त की जीवा AB अन्दर वाले वृत्त को बिन्दु C पर स्पर्श करती हैं, तो जीवा AB की माप ज्ञात कीजिए।
 View Solution
View SolutionThe length of the radius of circle is 5 cm and length of its chord AB is 8 cm . Calculate the distance of the chord AB form the centre O.
View SolutionThe angle subtended at the centre of a circle , by a chord whose length is equal to the radius of the circle will be
View SolutionIn circle with centre O , if AB is chord then angle subtend by chord AB at centre is
02:53View SolutionIn circle, if AB and CDare equal chords then angle subtended by chord AB is
03:16View SolutionIf chords AB and CD of congruent circles subtend equal angles at their centres, then
03:49View SolutionA chord AB is drawn in a circle with centre O and radius 5 cm. If the shortest distance between centre and chord is 4 cm, find the length of chord AB?
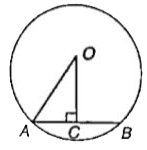
07:46View SolutionIn the given figure, O is the centre of the circle. Radius of the circle is 17 cm. lf OC=8cm, then the length of the chord AB is :
 03:50View Solution
03:50View SolutionO is the centre of a circle. AB is a chord of the circle but not its diameter. OC is perpendicular to AB. If OC = CB and radius of the circle be 7 cm, then the length of AB is
02:13View Solution

