Calculate the mean of the distribution, given below, using the short cut method:
The correct Answer is:46.9
To calculate the mean of the given distribution using the shortcut method, follow these steps:
Step 1: Create a Frequency Distribution Table
First, we need to set up a table with the class intervals and their corresponding frequencies.
| Class Interval | Frequency (F) |
|----------------|---------------|
| 11 - 20 | 2 |
| 21 - 30 | 6 |
| 31 - 40 | 10 |
| 41 - 50 | 12 |
| 51 - 60 | 9 |
| 61 - 70 | 7 |
| 71 - 80 | 4 |
Step 2: Calculate the Mid Values (X)
Next, we calculate the mid value for each class interval using the formula:
Mid Value=Lower Limit+Upper Limit2
| Class Interval | Mid Value (X) |
|----------------|----------------|
| 11 - 20 | 15.5 |
| 21 - 30 | 25.5 |
| 31 - 40 | 35.5 |
| 41 - 50 | 45.5 |
| 51 - 60 | 55.5 |
| 61 - 70 | 65.5 |
| 71 - 80 | 75.5 |
Step 3: Assume a Mean (A)
We need to assume a mean (A). The middle class interval is 41 - 50, so we take the mid value of this class as our assumed mean:
A=45.5
Step 4: Calculate the Deviation (D)
Now, we calculate the deviation (D) for each mid value using the formula:
D=X−A
| Mid Value (X) | Deviation (D = X - A) |
|----------------|------------------------|
| 15.5 | -30 |
| 25.5 | -20 |
| 35.5 | -10 |
| 45.5 | 0 |
| 55.5 | 10 |
| 65.5 | 20 |
| 75.5 | 30 |
Step 5: Calculate FD (Frequency × Deviation)
Next, we calculate the product of frequency (F) and deviation (D) for each class.
| Frequency (F) | Deviation (D) | FD (F × D) |
|----------------|----------------|------------|
| 2 | -30 | -60 |
| 6 | -20 | -120 |
| 10 | -10 | -100 |
| 12 | 0 | 0 |
| 9 | 10 | 90 |
| 7 | 20 | 140 |
| 4 | 30 | 120 |
Step 6: Sum of FD and Sum of Frequencies
Now, we sum up the FD column and the frequency column.
- Sum of FD = -60 - 120 - 100 + 0 + 90 + 140 + 120 = 70
- Sum of Frequencies (ΣF) = 2 + 6 + 10 + 12 + 9 + 7 + 4 = 50
Step 7: Calculate the Mean
Finally, we can calculate the mean using the shortcut formula:
Mean=A+ΣFDΣF
Substituting the values we have:
Mean=45.5+7050
Mean=45.5+1.4=46.9
Final Answer
The mean of the distribution is 46.9.
---
First, we need to set up a table with the class intervals and their corresponding frequencies.
|----------------|---------------|
| 11 - 20 | 2 |
| 21 - 30 | 6 |
| 31 - 40 | 10 |
| 41 - 50 | 12 |
| 51 - 60 | 9 |
| 61 - 70 | 7 |
| 71 - 80 | 4 |
Next, we calculate the mid value for each class interval using the formula:
Mid Value=Lower Limit+Upper Limit2
|----------------|----------------|
| 11 - 20 | 15.5 |
| 21 - 30 | 25.5 |
| 31 - 40 | 35.5 |
| 41 - 50 | 45.5 |
| 51 - 60 | 55.5 |
| 61 - 70 | 65.5 |
| 71 - 80 | 75.5 |
We need to assume a mean (A). The middle class interval is 41 - 50, so we take the mid value of this class as our assumed mean:
A=45.5
Now, we calculate the deviation (D) for each mid value using the formula:
D=X−A
|----------------|------------------------|
| 15.5 | -30 |
| 25.5 | -20 |
| 35.5 | -10 |
| 45.5 | 0 |
| 55.5 | 10 |
| 65.5 | 20 |
| 75.5 | 30 |
Next, we calculate the product of frequency (F) and deviation (D) for each class.
|----------------|----------------|------------|
| 2 | -30 | -60 |
| 6 | -20 | -120 |
| 10 | -10 | -100 |
| 12 | 0 | 0 |
| 9 | 10 | 90 |
| 7 | 20 | 140 |
| 4 | 30 | 120 |
Now, we sum up the FD column and the frequency column.
- Sum of Frequencies (ΣF) = 2 + 6 + 10 + 12 + 9 + 7 + 4 = 50
Finally, we can calculate the mean using the shortcut formula:
Mean=A+ΣFDΣF
Mean=45.5+7050
Mean=45.5+1.4=46.9
The mean of the distribution is 46.9.
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (C)
10 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (A)
17 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
Calculate the mean of the following distribution :

View SolutionCalculate the mean of the following distribution:
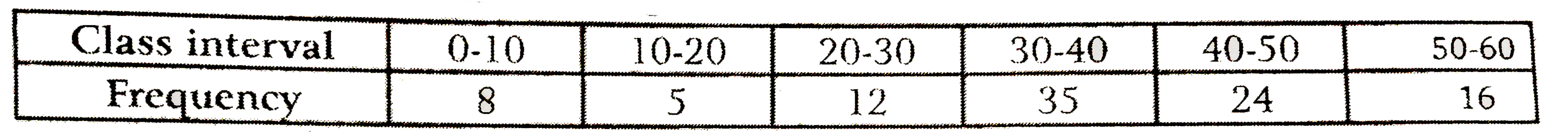
View SolutionSolve using short cut methods: 54×35
View SolutionSolve using short cut methods: 74×25
View SolutionCalculate the mean mark in the distribution given below:

Also, state the modal class.
View SolutionSolve using short cut methods: 64×125
View SolutionSolve using short cut methods: 47×999
View SolutionSolve using short cut methods: 246×15
View SolutionCalculate the mean for the following distribution:
View SolutionFind the mean from the following distribution table using short cut method :

View Solution
