If P={x:x∈W and 4≤x≤8} and Q={x:x∈N and x<6}. Find :
(i) P∪Q and P∩Q
(ii) Is (P∪Q)⊃(P∩Q) ?
The correct Answer is:P∪Q={1,2,3,4,5,6,7,8} and P∩Q={4,5}, (ii) yes
To solve the given problem, we will follow these steps:
Step 1: Define the sets P and Q
- Set P: This set consists of whole numbers x such that 4≤x≤8.
Therefore, P={4,5,6,7,8}.
- Set Q: This set consists of natural numbers x such that x<6.
Therefore, Q={1,2,3,4,5}.
Step 2: Find P∪Q (Union of P and Q)
The union of two sets includes all the elements from both sets without repetition.
- P∪Q={4,5,6,7,8}∪{1,2,3,4,5}
Combining these sets, we get:
- P∪Q={1,2,3,4,5,6,7,8}
Step 3: Find P∩Q (Intersection of P and Q)
The intersection of two sets includes only the elements that are present in both sets.
- P∩Q={4,5,6,7,8}∩{1,2,3,4,5}
The common elements are:
- P∩Q={4,5}
Step 4: Check if P∪Q is a subset of P∩Q
We need to determine if P∪Q⊆P∩Q.
- We found P∪Q={1,2,3,4,5,6,7,8}
- We found P∩Q={4,5}
Since P∪Q contains elements (1, 2, 3, 6, 7, 8) that are not in P∩Q, we conclude that:
- P∪Q is not a subset of P∩Q.
Final Answers:
1. P∪Q={1,2,3,4,5,6,7,8}
2. P∩Q={4,5}
3. No, P∪Q is not a subset of P∩Q.
---
Therefore, P={4,5,6,7,8}.
Therefore, Q={1,2,3,4,5}.
- We found P∩Q={4,5}
2. P∩Q={4,5}
3. No, P∪Q is not a subset of P∩Q.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - SETS EXERCISE - EXERCISE 6( E)11videos
SETS
- BOOK - ICSECHAPTER - SETS EXERCISE - EXERCISE 6( C)11videos
SETS
- BOOK - ICSECHAPTER - REPRESENTING 3-D IN 2 -DEXERCISE - EXCERSICE13videos
REPRESENTING 3-D IN 2 -D
- BOOK - ICSECHAPTER - SPECIAL TYPES OF QUADRILATERALSEXERCISE - EXERCISE22videos
SPECIAL TYPES OF QUADRILATERALS
Similar Questions
If A = {5, 6, 7, 8, 9}, B={x:3<x<8 and x∈W} and C={x:x≤5 and x∈N}. Find :
(i) A∪B and (A∪B)∪C
(ii) B∪C and A∪(B∪C)
(iii) A∩B and (A∩B)∩C
(iv) B∩C and A∩(B∩C)
Is (A∪B)∪C=A∪(B∪C)?
Is (A∩B)∩C)=A∩(B∩C)?View SolutionIf A={x∈W:5<x<10},B={3,4,5,6,7} and C={x=2n,n∈N and n≤4}. Find:
(i) A∩(B∪C), (ii) (B∪A)∩(B∪C)
(iii) B∪(A∩C), (iv) (A∩B)∪(A∩C)
Name the sets which are equal.View SolutionIf P = {factors of 36} and Q = {factors of 48}, find :
(i) P∪Q, (ii) P∩Q, (iii) Q−P , (iv) P'∩QView SolutionLet P = { x: x is a factor of 18 } and Q = { x : x is a factor of 24}.
Find : (a) P∪Q
(b) P∩QView SolutionGiven A={x∈N:x<6},B={3,6,9} and C={x∈N:2x−5≤8}. Show that:
(i) A∪(B∩C)=(A∪B)∩(A∪C)
(ii) A∩(B∪C)=(A∩B)∪(A∩C)View SolutionIf P {x : x is a letter in the word CHANDIGARH } and Q = {x : x is a letter in the word JAMNAGAR }, then
find P∪QandP∩QView SolutionIf A = {x∣x∈B,x≤10} and B = {x∣x∈W,x≤15andx is a multiple of 5 } , then
find n(A) , n(B) , n(A∪B)andn(A∩B)View SolutionIf P {x : x is a letter in the word CHANDIGARH } and Q = {x : x is a letter in the word JAMNAGAR }, then
find n(P) , n(Q) n(P∪Q)andn(P∩Q)View SolutionIf P = {all months of a year } and Q = {months of a year whose name begin with letter M } find P∪QandP∩Q State whether the sets P and Q are joint or disjoint sets .
View SolutionFrom the adjoining Venn , diagram , find the following sets :
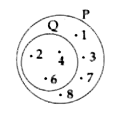
(i) P (ii) Q (iii) P∪Q (iv) P∩QView Solution

