Find the odd one out in each group. a. Methionine, Tryptophan, Valine, Alanine. b. Collagen, Actin, Myosin, Glutelin, Serine. c. Maltose, Sucrose, Lactose, Cellulose. d. Oxido reductase, Transferase, Lyase, Ligase, Maltase.
a. Alanine (non-essential amino acid) b. Serine c. Cellulose d. Maltose
Similar Questions
The following words are from the text you have read. The synonyms for each word are given. Find the odd one out.
(a) serious, grave, ridiculous, stern, solemn
(b) suitable, unfitting, appropriate, right, proper
(c ) hostile, unfriendly, averse, agreeable, unreceptive
(d) peaceful, harmonious, quiet, serene, violent
(e) appalling, atrocious, wonderful, awful, dreadful
View SolutionThe English alphabet is categorised into 5 groups, each starting with a vowel and encompassing the immediately following consonants in the group. Thus, the first group would have letters A, B,C and D, the second E, F, G and H, and so on. These groups are assigned values as 10 for the first, 20 for the second, and so on, up to 50 the last. Every letter in a particular group will have the same value of the group when used to form words. The value of each letter should add up to compute the value of the word. If the word has letters only from the same group, the value of the word would be the value of the letter multiplied by the number of letters in the word. However, if the letters in a word are from different groups, the value of the first letter of the word and any other letter of that group will be the same as that of its group, but that of the subsequent letter will he ‘double’ as much as the value of its group. For example: The value of ‘CAB’ will be 30 (i.e. 10+10+10) as all the three letters are from the first group, each one having a value of 10. The value of ‘BUT’ will be 10+(50⋅2)+(40⋅2)=190 The value of ‘JUNK’ will be 30+(50⋅2)+30+30=190. Now, find out the value of each word in the following questions
which one or two or three of the words denoted by A, B, C correspond to the given value ?
80
(A)HEAD
(B)AHEAD
(C)ODD
1) A and B only
2) B and C only
3) A and C only
4) All the three
5) None of these
View SolutionThe English alphabet is categorised into 5 groups, each starting with a vowel and encompassing the immediately following consonants in the group. Thus, the first group would have letters A, B,C and D, the second E, F, G and H, and so on. These groups are assigned values as 10 for the first, 20 for the second, and so on, up to 50 the last. Every letter in a particular group will have the same value of the group when used to form words. The value of each letter should add up to compute the value of the word. If the word has letters only from the same group, the value of the word would be the value of the letter multiplied by the number of letters in the word. However, if the letters in a word are from different groups, the value of the first letter of the word and any other letter of that group will be the same as that of its group, but that of the subsequent letter will he ‘double’ as much as the value of its group. For example: The value of ‘CAB’ will be 30 (i.e. 10+10+10) as all the three letters are from the first group, each one having a value of 10. The value of ‘BUT’ will be 10+(50⋅2)+(40⋅2)=190 The value of ‘JUNK’ will be 30+(50⋅2)+30+30=190. Now, find out the value of each word in the following questions:
SHOP
1) 70
2) 120
3) 130
4) 140
5) None of these
View SolutionThe English alphabet is categorised into 5 groups, each starting with a vowel and encompassing the immediately following consonants in the group. Thus, the first group would have letters A, B,C and D, the second E, F, G and H, and so on. These groups are assigned values as 10 for the first, 20 for the second, and so on, up to 50 the last. Every letter in a particular group will have the same value of the group when used to form words. The value of each letter should add up to compute the value of the word. If the word has letters only from the same group, the value of the word would be the value of the letter multiplied by the number of letters in the word. However, if the letters in a word are from different groups, the value of the first letter of the word and any other letter of that group will be the same as that of its group, but that of the subsequent letter will he ‘double’ as much as the value of its group. For example: The value of ‘CAB’ will be 30 (i.e. 10+10+10) as all the three letters are from the first group, each one having a value of 10. The value of ‘BUT’ will be 10+(50⋅2)+(40⋅2)=190 The value of ‘JUNK’ will be 30+(50⋅2)+30+30=190. Now, find out the value of each word in the following questions:
HIGH
1) 40
2) 60
3) 70
4) 80
5) None of these
View SolutionThe English alphabet is categorised into 5 groups, each starting with a vowel and encompassing the immediately following consonants in the group. Thus, the first group would have letters A, B,C and D, the second E, F, G and H, and so on. These groups are assigned values as 10 for the first, 20 for the second, and so on, up to 50 the last. Every letter in a particular group will have the same value of the group when used to form words. The value of each letter should add up to compute the value of the word. If the word has letters only from the same group, the value of the word would be the value of the letter multiplied by the number of letters in the word. However, if the letters in a word are from different groups, the value of the first letter of the word and any other letter of that group will be the same as that of its group, but that of the subsequent letter will he ‘double’ as much as the value of its group. For example: The value of ‘CAB’ will be 30 (i.e. 10+10+10) as all the three letters are from the first group, each one having a value of 10. The value of ‘BUT’ will be 10+(50⋅2)+(40⋅2)=190 The value of ‘JUNK’ will be 30+(50⋅2)+30+30=190. Now, find out the value of each word in the following questions:
SPORT
1) 200
2) 360
3) 380
4) 250
5) None of these
View SolutionThe English alphabet is categorised into 5 groups, each starting with a vowel and encompassing the immediately following consonants in the group. Thus, the first group would have letters A, B,C and D, the second E, F, G and H, and so on. These groups are assigned values as 10 for the first, 20 for the second, and so on, up to 50 the last. Every letter in a particular group will have the same value of the group when used to form words. The value of each letter should add up to compute the value of the word. If the word has letters only from the same group, the value of the word would be the value of the letter multiplied by the number of letters in the word. However, if the letters in a word are from different groups, the value of the first letter of the word and any other letter of that group will be the same as that of its group, but that of the subsequent letter will he ‘double’ as much as the value of its group. For example: The value of ‘CAB’ will be 30 (i.e. 10+10+10) as all the three letters are from the first group, each one having a value of 10. The value of ‘BUT’ will be 10+(50⋅2)+(40⋅2)=190 The value of ‘JUNK’ will be 30+(50⋅2)+30+30=190. Now, find out the value of each word in the following questions
which one or two or three of the words denoted by A, B, C correspond to the given value ?
200
(A)HOW
(B)SKY
(C)BEGAY
1) A and B only
2) B and C only
3) A and C only
4) All the three
5) None of these
View SolutionThe English alphabet is categorised into 5 groups, each starting with a vowel and encompassing the immediately following consonants in the group. Thus, the first group would have letters A, B,C and D, the second E, F, G and H, and so on. These groups are assigned values as 10 for the first, 20 for the second, and so on, up to 50 the last. Every letter in a particular group will have the same value of the group when used to form words. The value of each letter should add up to compute the value of the word. If the word has letters only from the same group, the value of the word would be the value of the letter multiplied by the number of letters in the word. However, if the letters in a word are from different groups, the value of the first letter of the word and any other letter of that group will be the same as that of its group, but that of the subsequent letter will he ‘double’ as much as the value of its group. For example: The value of ‘CAB’ will be 30 (i.e. 10+10+10) as all the three letters are from the first group, each one having a value of 10. The value of ‘BUT’ will be 10+(50⋅2)+(40⋅2)=190 The value of ‘JUNK’ will be 30+(50⋅2)+30+30=190. Now, find out the value of each word in the following questions
which one or two or three of the words denoted by A, B, C correspond to the given value ?
90
(A)BEG
(B)WAD
(C)NOD
1) A and B only
2) B and C only
3) A and C only
4) All the three
5) None of these
View SolutionIn each question below, a group of digits/symbols is given, followed by four combinations of letters numbered (a), (b), (c) and (d). You have to find out which of the combinations (a), (b), (c) and (d) correctly represents the group of digits/symbols based on the following coding system and the conditions those follow and mark the number of that combination as your answer. If none of the four combinations correctly represents the group of digits/symbols, mark (e) i.e., "None of these as the answer
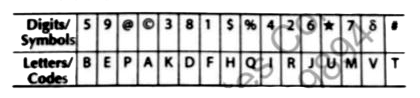
Conditions
(i) If the first unit in the group is an even digit and the last unit is a symbol, both these are to be coded as the code for the symbol.
(ii) If the first unit in the group is an odd digit and the last unit is an even digit their codes are to be interchanged.
(iii) If both the first and the last units in the group are symbols, both these are to be coded as or
387#(c)9
View SolutionIn each question below, a group of digits/symbols is given, followed by four combinations of letters numbered (a), (b), (c) and (d). You have to find out which of the combinations (a), (b), (c) and (d) correctly represents the group of digits/symbols based on the following coding system and the conditions those follow and mark the number of that combination as your answer. If none of the four combinations correctly represents the group of digits/symbols, mark (e) i.e., "None of these as the answer
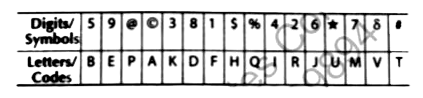
Conditions
(i) If the first unit in the group is an even digit and the last unit is a symbol, both these are to be coded as the code for the symbol.
(ii) If the first unit in the group is an odd digit and the last unit is an even digit their codes are to be interchanged.
(iii) If both the first and the last units in the group are symbols, both these are to be coded as or
@91$26
View SolutionIn each question below, a group of digits/symbols is given, followed by four combinations of letters numbered (a), (b), (c) and (d). You have to find out which of the combinations (a), (b), (c) and (d) correctly represents the group of digits/symbols based on the following coding system and the conditions those follow and mark the number of that combination as your answer. If none of the four combinations correctly represents the group of digits/symbols, mark (e) i.e., "None of these as the answer
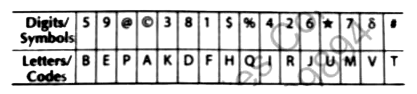
Conditions
(i) If the first unit in the group is an even digit and the last unit is a symbol, both these are to be coded as the code for the symbol.
(ii) If the first unit in the group is an odd digit and the last unit is an even digit their codes are to be interchanged.
(iii) If both the first and the last units in the group are symbols, both these are to be coded as or
4@312 ∂
View Solution
