ABC is a triangle in vertical plane. Its two base angles ∠BAC and ∠BCA are 45∘ and tan−1(1/3) respectively. A particle is projected from point A such that it passes through vertices B and C. Find angle of projection in degrees:
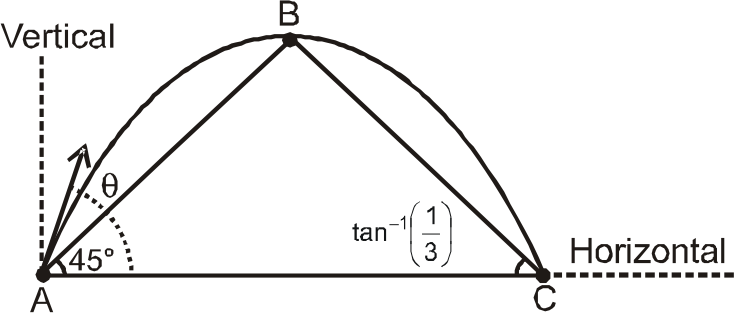
60∘
53∘
tan−1(5/4)
tan−1(5/3)
The correct Answer is:B
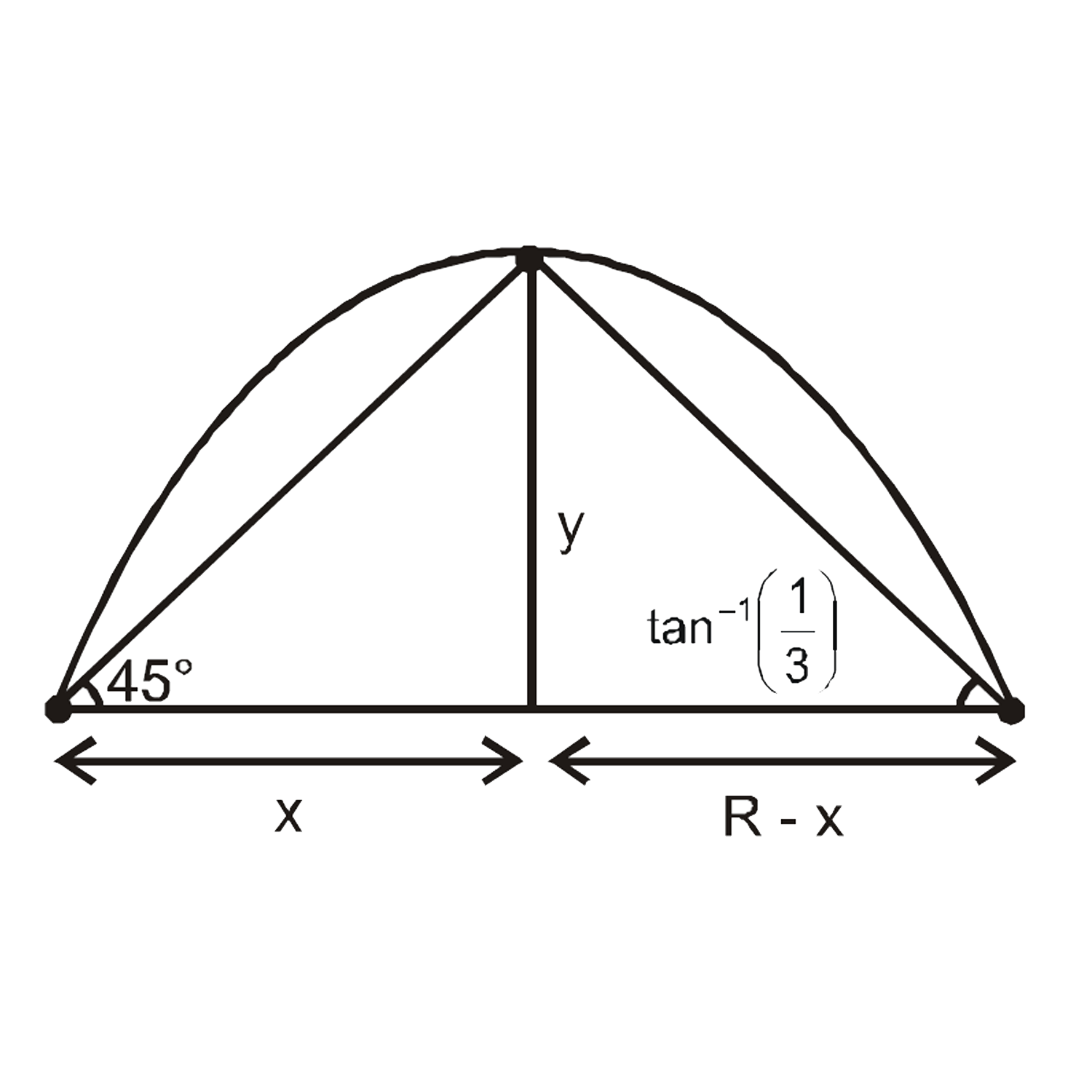
equation y=xtanθ(1−xR)
at Bx=y
tanθ=RR−Y .....(i)
tan45∘=YX
x=y .....(ii)
(13)=YR−x ....(iii)
Solving equation 2 and 3
R=4y=4x {it om (i)
tanθ=RR−R4
tanθ=43
θ=53∘
Topper's Solved these Questions
Similar Questions
If two angles of a triangle are tan−1(2)andtan−1(3), then find the third angles
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionIn triangle ABC, the co-ordinates of vertices A, B and C are (4, 7), (-2, 3) and (0, 1) respectively. Find the equation of median through vertex A.
Also, find the equation of the line through vertex B and parallel to AC.
View SolutionIf the vertices A,B,C of a triangle ABC are (1,2,3),(-1,0,0) ,(0,1,2) , respectively, then find ∠ABC.
View SolutionIn an isosceles triangle, each base angle is four times its vertical angle. Find each angle of the triangle.
View SolutionThe vertical angle of an isosceles triangle is 1000. Find its base angles.
View SolutionThe position vectors of vertices of △ABC are (1,−2),(−7,6)and(115,25) respectively. The measure of the interior angle A of the △ABC, is,
View SolutionEach base angle of an isosceles triangle is 15∘ more than its vertical angle. Find each angle of the triangle.
View SolutionThe vertical angle of an isosceles triangle is twice the sum if its base angles. Find each angle of the triangle.
View SolutionThe vertices of ABC are (−2, 1), (5, 4) and (2, −3) respectively. Find the area of the triangle and the length of the altitude through A .
View Solution
