Two particles are moving in different circles in same plane with different angular velocities as shown in figure. At t = 0, initial positions of particles A and B are shown by dots on the respective circles. Initial distance between particles is 1m. Particle A move anticlockwise in the first circle whereas B moves clockwise in the second circle. Angle described (rotated) by A and B in time 't' are θA=(π2t) and θB=(πt) respectively. here θ is in radian and t is in second. Radius of each circle is shown in diagram.
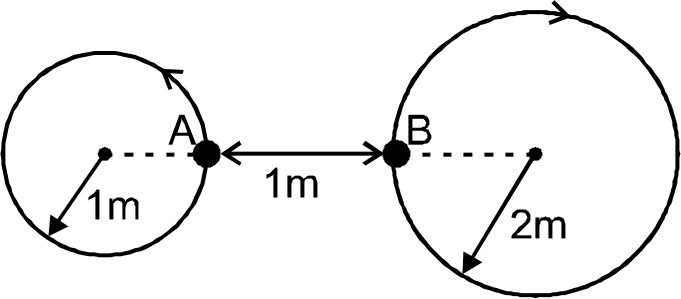
At time t=2 second, the angular velocity of the particle A with respect to the particle B is
π23m/s
π27
π24
None of these
At time t=1 s positions of A and B are
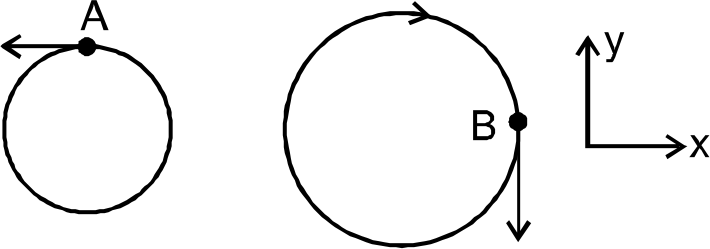
Acceleration of A →aA=ω21r1(−ˆj)=(π2)2(1)(−ˆj)
Topper's Solved these Questions
Similar Questions
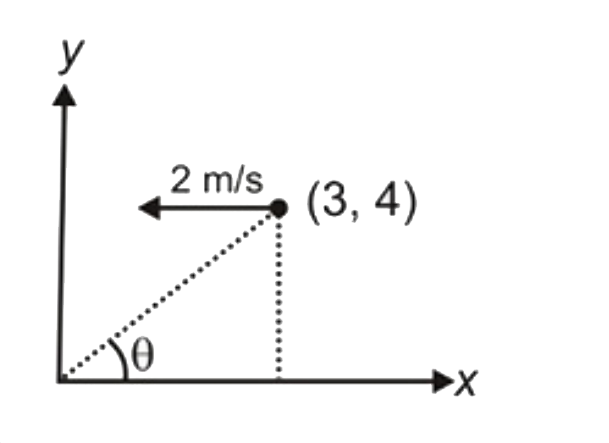
A particle is moving in x-y plane as shown in the figure. Angular velocity of the particle with respect to the origin is
View SolutionA particle is moving in a circle with uniform speed its motion is
View SolutionParticles AandB move with constant and equal speeds in a circle as shown in (Fig. 5.164). Find the angular velocity of the particle A with respect to B, if the angular velocity of particle Aw.r.t.O is ω.
 .
.
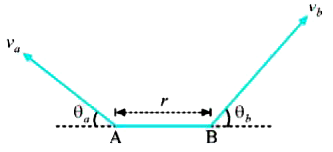
View SolutionTwo particles A and B are moving as shown in figure. At this moment of time, the angular speed of A with respect to B is?
View SolutionA particle is moving in a circle:
View SolutionA particle is moving in a circle in front of a plane mirror in the situation as shown in figure. The plane of motion of the particle is perpendicular to the plane of mirror. Then the motion of image of particle with respected to the partickle is

View SolutionTwo particles A and B moving in a plane have velocities as shown in figure .Relative velocity of A w.r.t B
View SolutionTwo particles AandB are moving with uniform velocity as shown in (Fig. 5.130) given below at t=0.
(a) Will the two particles collide ?
(b) Find out the shortest distance between two particles.
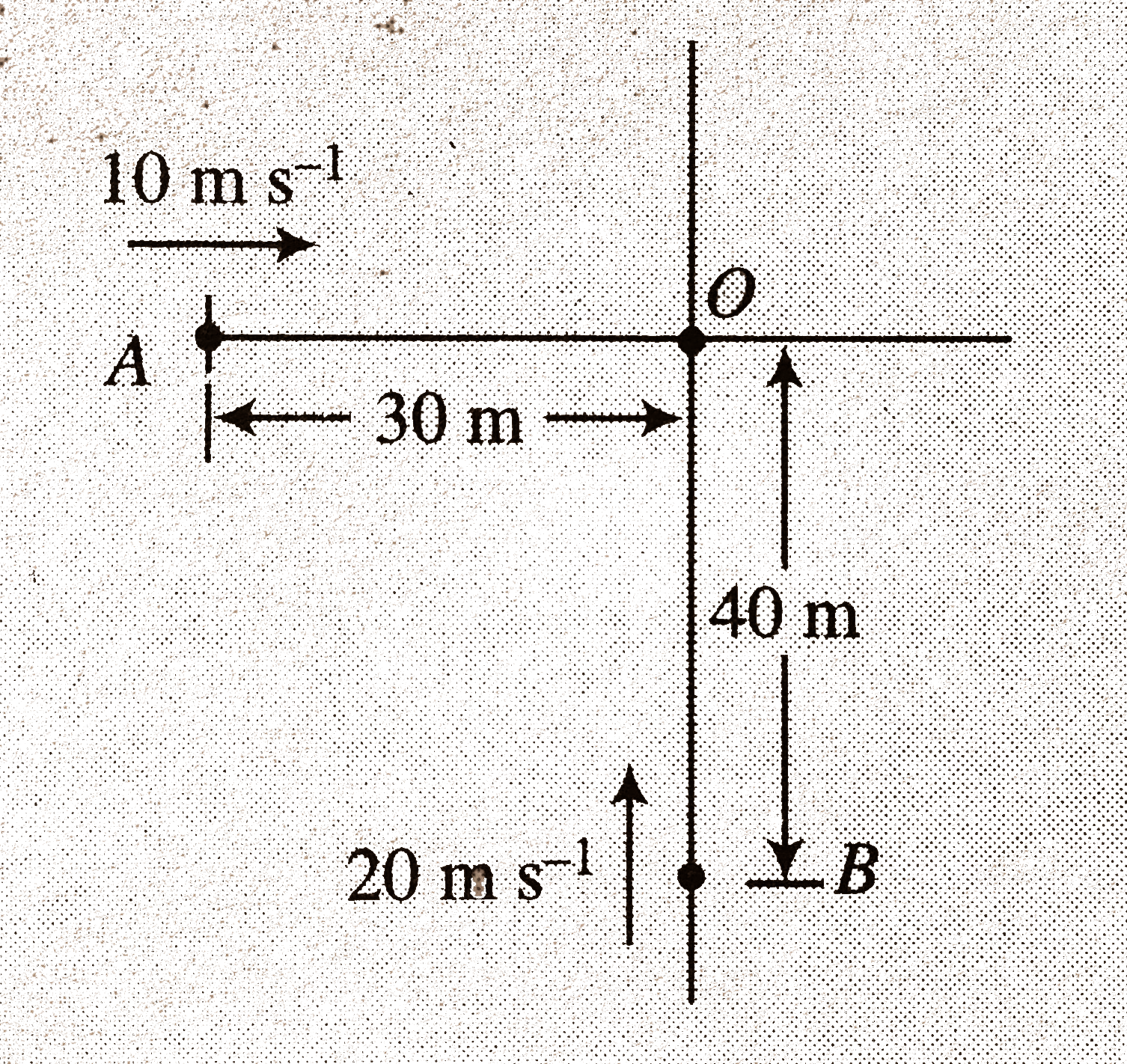 .
.
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
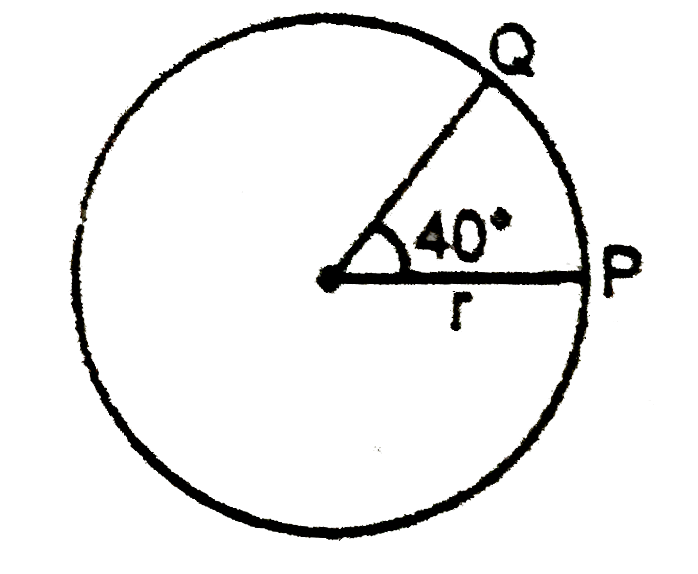
View SolutionA particle is moving in a circle of radius r with speed v as shown in the figure. The magnitude of change in velocity in moving from P to Q is
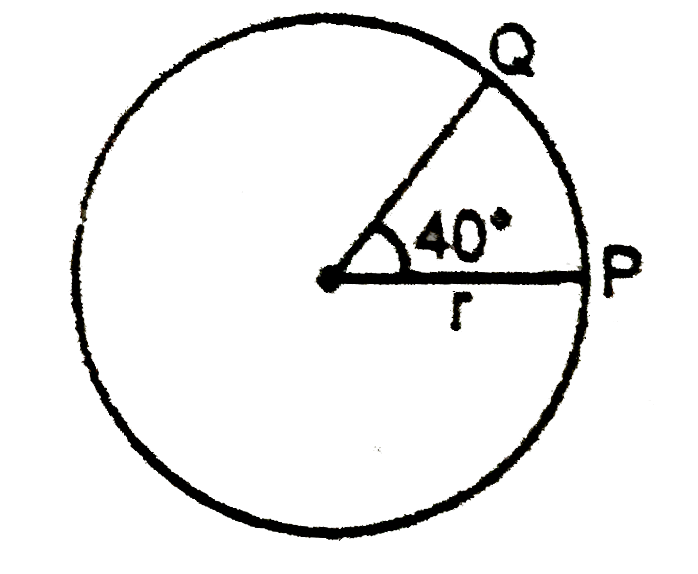
View Solution
