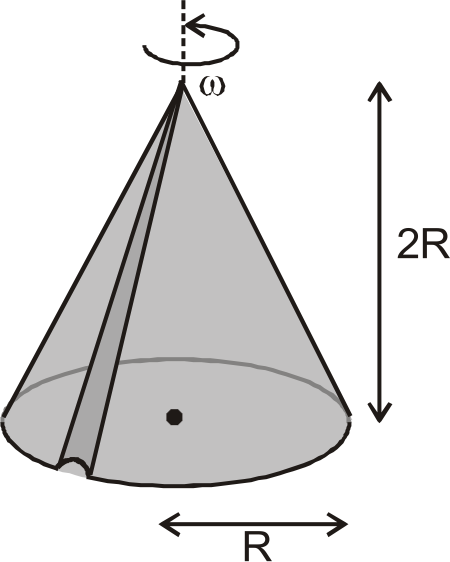
A uniform solid cone of mass m, base radius ‘R’ and height 2R, has a smooth groove along its slant height as shown in figure. The cone is rotating with angular speed ω, about the axis of symmetry. If a particle of mass ‘m’ is released from apex of cone, to slide along the groove, then angular speed of cone when particle reaches to the base of cone is
3ω13
4ω13
5ω13
9ω13
Initially
I1=310mR2&ω1=ω
Finally I2=1310mR2&ω2=ωnew
Using conservation of anular momentum
I1ω1=I2ω2
ω2=ωnew=3ω13
Topper's Solved these Questions
Similar Questions
Knowledge Check
A cone has a slant height of 8 and a lateral area of 48π. What is the radius of the base of the cone ?
A3B6C12D16
A wheel of moment of inertial I and radius R is rotating about its axis at an angular speed ω. It picks up a stationary particle of mass m at its edge. Find the new angular speed of the wheel.
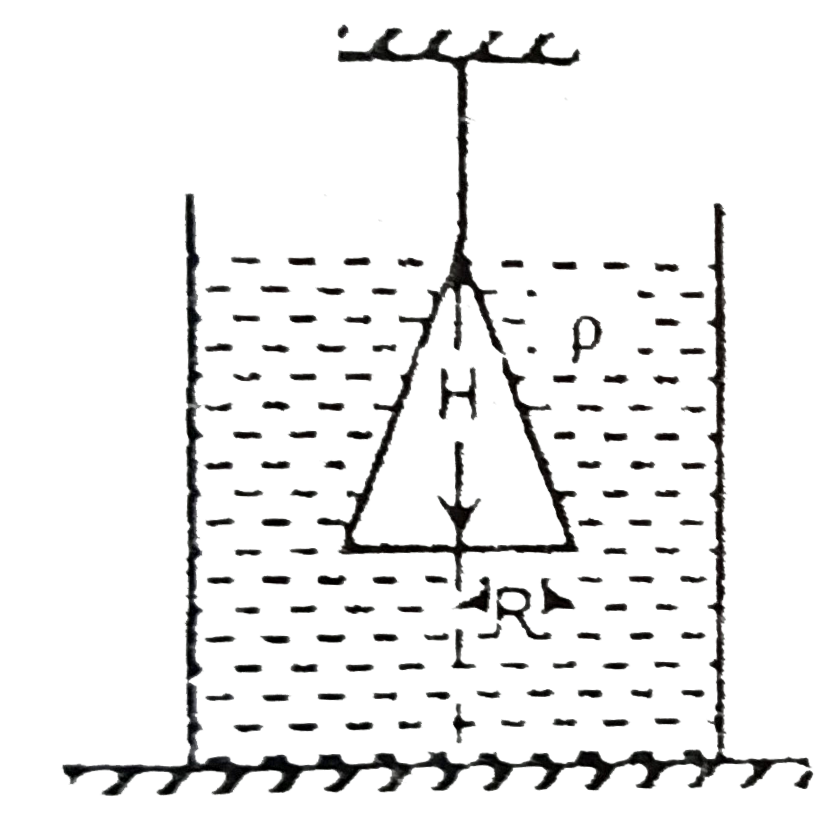
View SolutionA cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
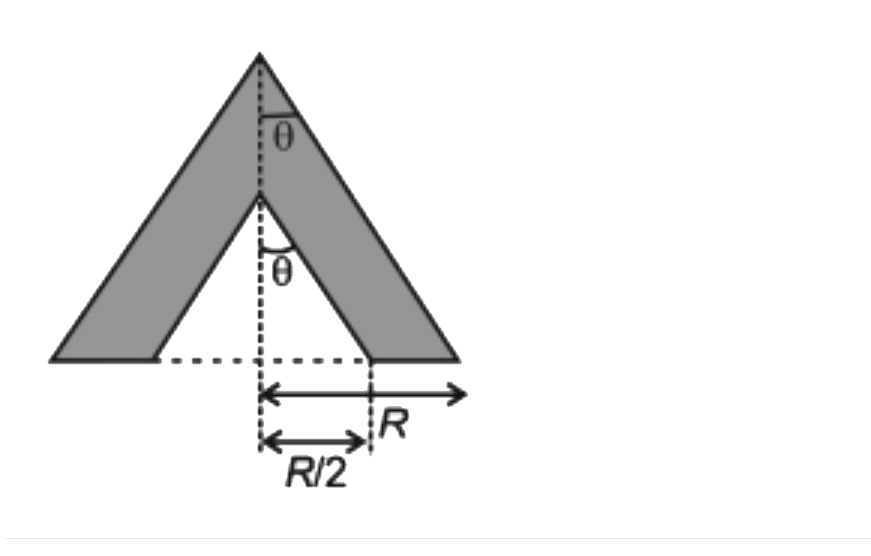
View SolutionFrom a uniform solid cone of base radius R and height H, a symmetric cone of the base radius R2 is removed as shown. Then the centre of mass is shifted by H/n. Find the value of of n.
View SolutionThe ratio of the base radius and height of a cone is 5 : 12. Find its slant height and radius if its volume is 800πm3.
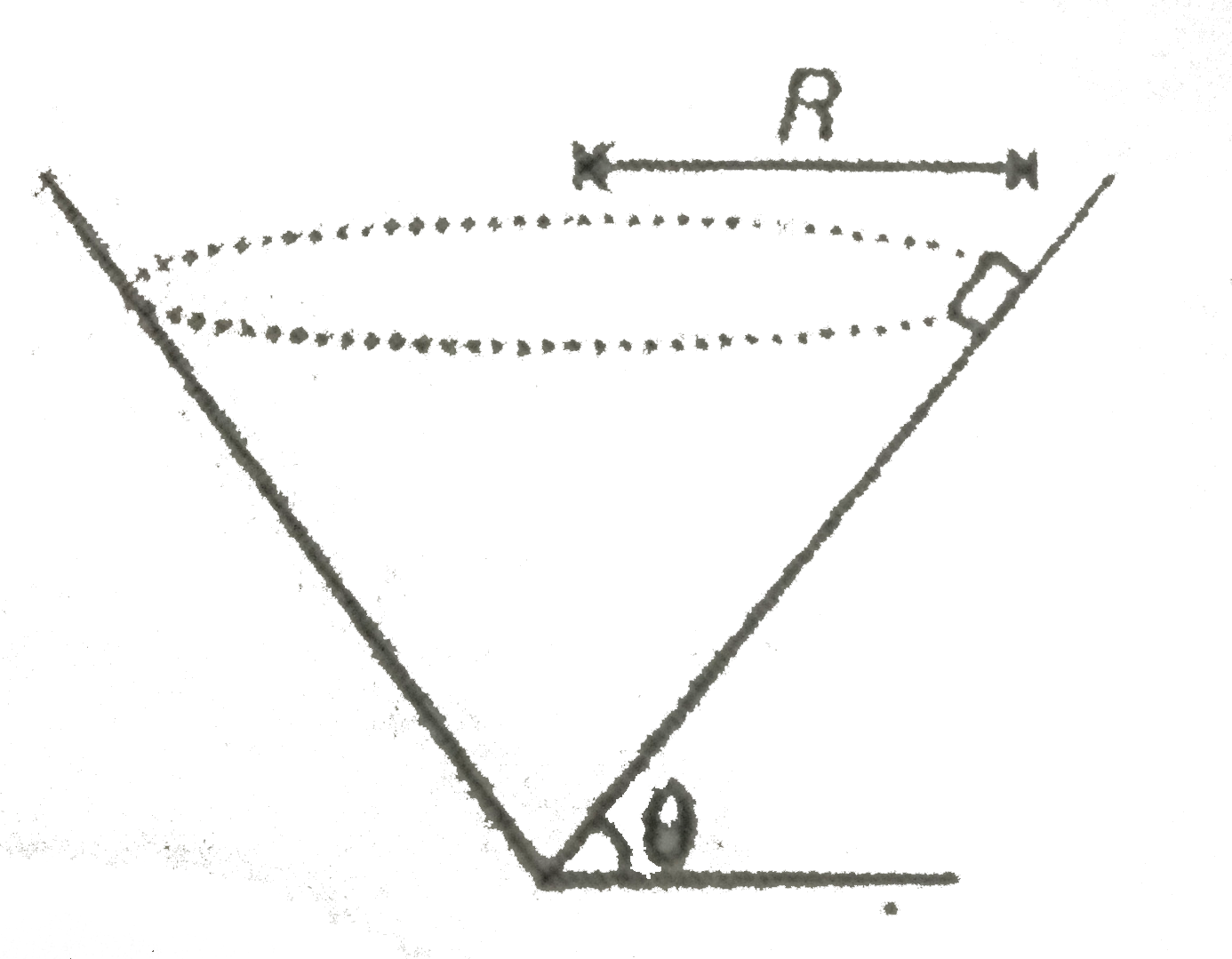
View SolutionA block of mass m is moving in a circle of radius R with speed v inside a smooth cone as shown in figure. Choose the wrong options
View SolutionA cylinder and a cone are of the same base radius and of same height. Find the ratio of the volume of the cylinder to that of the cone.
View SolutionA particle is at rest with respect to the wall of an inverted cone rotating with uniform angular velocity ω about its central axis. The displacement of particle along the surface up or down, the equilibrium of particle is

View Solution
