A substance is found to hav a magnetic moments of 3.9BM.How many unpaired electrons does it contain?
The correct Answer is:μB(3.9)=,n=3
To solve the problem of determining the number of unpaired electrons in a substance with a magnetic moment of 3.9 Bohr magnetons (BM), we can follow these steps:
1. Understand the Formula for Magnetic Moment:
The magnetic moment (μ) is related to the number of unpaired electrons (n) by the formula:
μ=√n(n+2)
Given that the magnetic moment is 3.9 BM, we can set up the equation:
3.9=√n(n+2)
2. Square Both Sides:
To eliminate the square root, we square both sides of the equation:
(3.9)2=n(n+2)
This simplifies to:
15.21=n(n+2)
3. Rearrange the Equation:
Rearranging gives us a standard quadratic equation:
n2+2n−15.21=0
4. Use the Quadratic Formula:
The quadratic formula is given by:
n=−b±√b2−4ac2a
Here, a=1, b=2, and c=−15.21. Plugging in these values:
n=−2±√(2)2−4⋅1⋅(−15.21)2⋅1
5. Calculate the Discriminant:
First, calculate the discriminant:
b2−4ac=4+60.84=64.84
6. Find the Square Root:
Calculate the square root of the discriminant:
√64.84≈8.06
7. Substitute Back into the Formula:
Now substitute back into the quadratic formula:
n=−2±8.062
8. Calculate Possible Values for n:
This gives us two potential solutions:
n1=6.062≈3.03(take the positive root)
n2=−10.062(discard as it is negative)
9. Round to the Nearest Whole Number:
Since the number of unpaired electrons must be a whole number, we round 3.03 to 3.
Final Answer:
The substance contains 3 unpaired electrons.
The magnetic moment (μ) is related to the number of unpaired electrons (n) by the formula:
μ=√n(n+2)
Given that the magnetic moment is 3.9 BM, we can set up the equation:
3.9=√n(n+2)
To eliminate the square root, we square both sides of the equation:
(3.9)2=n(n+2)
This simplifies to:
15.21=n(n+2)
Rearranging gives us a standard quadratic equation:
n2+2n−15.21=0
The quadratic formula is given by:
n=−b±√b2−4ac2a
Here, a=1, b=2, and c=−15.21. Plugging in these values:
n=−2±√(2)2−4⋅1⋅(−15.21)2⋅1
First, calculate the discriminant:
b2−4ac=4+60.84=64.84
Calculate the square root of the discriminant:
√64.84≈8.06
Now substitute back into the quadratic formula:
n=−2±8.062
This gives us two potential solutions:
n1=6.062≈3.03(take the positive root)
n2=−10.062(discard as it is negative)
Since the number of unpaired electrons must be a whole number, we round 3.03 to 3.
The substance contains 3 unpaired electrons.
Topper's Solved these Questions
- D BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - D BLOCK ELEMENTSEXERCISE - EXERCISE-I PART-II
56 Videos
- D BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - D BLOCK ELEMENTSEXERCISE - EXERCISE-I PART-III
15 Videos
- D BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - D BLOCK ELEMENTSEXERCISE - BOARD LEVEL EXERCISE
21 Videos
- D & F BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - D & F BLOCK ELEMENTSEXERCISE - ORGANIC CHEMISTRY(Aldehydes , Ketones, Carboxylic acid)
15 Videos
- DPPBOOK - RESONANCE ENGLISHCHAPTER - DPPEXERCISE - QUESTIONS
368 Videos
Similar Questions
Knowledge Check
How many stereogenic centres does it contain ?
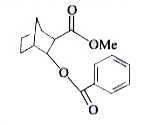 A1B2C3D4
A1B2C3D4
How many unpaired electrons are present in NO molecule ?
View SolutionA metal ion from the first transition series has a magnetic moment (calculated) of 2.83BM. How many unpaired electrons are expected to be presetn in the ion?
View SolutionA metal ion from the first transition series has a magnetic moment (calculated) as 3.87B.M. How many unpaired electrons are expected to be present in the ion?
View SolutionHow many types of proteins does membrane contain?
View SolutionHow many number of unpaired electrons are present in K+ ?
View SolutionHow many number of unpaired electrons are present in Ca2+ ?
View SolutionHow many number of unpaired electrons are present in Mn2+ ?
View Solution
