Given the visible green light has a wavelength of 510 nm then corresponding frequency and wave number are respectively (C=3×108ms−1) :
5.8×1014Hz,0.001nm
6×1016Hz,0.004nm−1
5.8×1014Hz,0.001nm−1
5×1012Hz,0.008nm
The correct Answer is:C
To solve the problem of finding the corresponding frequency and wave number for the visible green light with a wavelength of 510 nm, we will follow these steps:
Step 1: Convert Wavelength from Nanometers to Meters
The given wavelength (λ) is in nanometers. We need to convert it to meters for our calculations.
λ=510nm=510×10−9m
Step 2: Use the Speed of Light to Find Frequency
We can use the formula that relates the speed of light (C), frequency (ν), and wavelength (λ):
ν=Cλ
Where:
- C=3×108m/s
- λ=510×10−9m
Substituting the values:
ν=3×108m/s510×10−9m
Calculating this gives:
ν≈5.88×1014Hz
Step 3: Calculate Wave Number
The wave number (k) is defined as the reciprocal of the wavelength:
k=1λ
Using the wavelength in meters:
k=1510×10−9m
Calculating this gives:
k≈1.96×106m−1
Alternatively, if we want to express this in terms of nanometers:
k=1510nm≈0.00196nm−1
Final Answers
Thus, the corresponding frequency and wave number for the visible green light are:
- Frequency (ν) = 5.88×1014Hz
- Wave number (k) = 1.96×106m−1 or 0.00196nm−1
---
The given wavelength (λ) is in nanometers. We need to convert it to meters for our calculations.
We can use the formula that relates the speed of light (C), frequency (ν), and wavelength (λ):
- C=3×108m/s
- λ=510×10−9m
The wave number (k) is defined as the reciprocal of the wavelength:
Thus, the corresponding frequency and wave number for the visible green light are:
- Wave number (k) = 1.96×106m−1 or 0.00196nm−1
Similar Questions
Calculate the wavelength , frequency and wave number of a light wave whose time period is 3×10−10s.
View SolutionCalculate the wavelength, frequency, and wave number of a light wave whose period is 2.0×10−10s.
View SolutionCalculate the frequency , wave number of the microwaves with 4×107nm
View SolutionCalculate the frequency , wave number of the microwaves with wavelength 4×107nm
View SolutionA plane electromagnetic wave of frequency 25 GHz is propagating in vacuum along the z-direction. At a particular point in space and time, the magentic field is given by →B=5×10−8ˆiT. The corresponding electric field E is (speed of light c=3×108ms−1
View SolutionIn a historical experiment to determine Planck's constant, a metal surface was irradiated with light of different wavelengths. The emitted photoelectron energies were measured by applying a stopping potential. The relevant data for the wavelength (λ). ) of incident light and the corresponding stopping potential (V0) are given below :
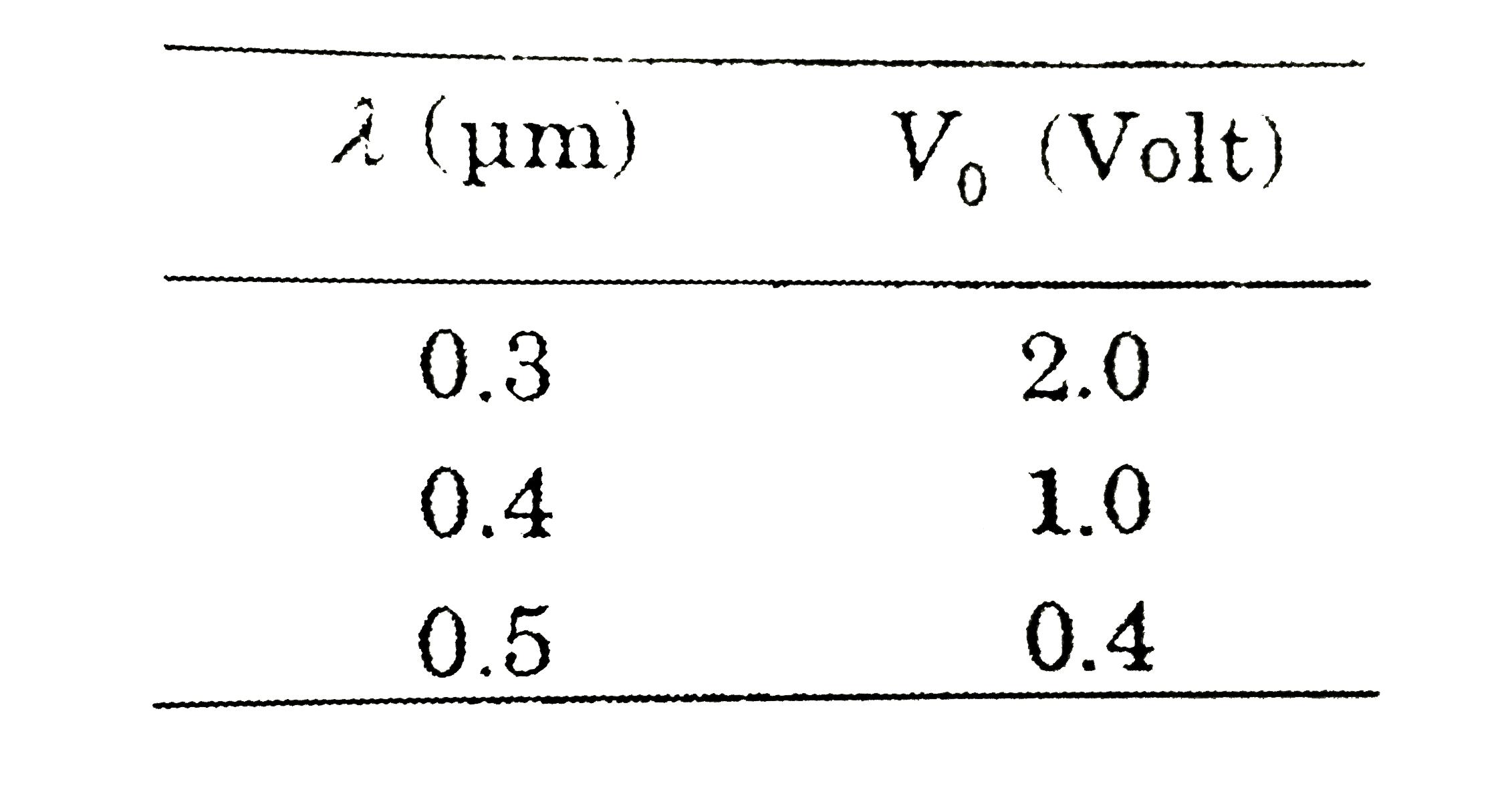
Given that c=3×108ms−1ande=1.6×10−19C Planck's constant (in units of J s) found from such an experiment is
View SolutionYellow light emitted from a sodium lamp has a wavelength ( λ ) of 580nm. Calculate the frequency (ν). Wave number and energy of yellow light photon .
View SolutionCalculate the wavelength of an ultraviolet wave , if its frequency is 12×1016 cycles per second and c=3×108ms−1?
View SolutionA plane wave front of yellow light with wavelength 0.5μm in air suffers refraction in a medium in which velocity of light is 2×108ms−1 them, the wavelength of the light associated with a wave front in the medium would be
View SolutionCalculate the frequency of yellow light of wavelength 550 nm. The speed of light is 3×108ms−1.
View Solution
