1 mol of an idel gas is allowed to expand isothermally at 27∘C till its volume is tripped. If the expansion is carried out reversibly then select the correct option(s) : (R=253JmolK,log3=0.48)
qsys=2763J/mol
ΔSsys.=7.21J/K mol
ΔSuniverse=0
ΔSsurr.=−9.21J/K mol
The correct Answer is:A, C, D
To solve the problem step by step, we will calculate the various thermodynamic quantities involved in the isothermal expansion of the ideal gas.
Step 1: Understand the Given Data
- Number of moles (n) = 1 mol
- Initial temperature (T) = 27°C = 300 K (since K = °C + 273)
- Volume is tripled, so if the initial volume is V, the final volume is 3V.
- Given R = 25/3 J/(mol·K)
- Given log(3) = 0.48
Step 2: Calculate the Change in Entropy of the System (ΔS_system)
The formula for the change in entropy for an isothermal process is:
ΔSsystem=nRln(VfinalVinitial)
Substituting the values:
ΔSsystem=1⋅253⋅2.303⋅log(3)
Calculating:
ΔSsystem=1⋅253⋅2.303⋅0.48
ΔSsystem=25⋅2.303⋅0.483
ΔSsystem≈9.21J/(K⋅mol)
Step 3: Calculate the Change in Entropy of the Surroundings (ΔS_surrounding)
For a reversible process, the total change in entropy of the universe is zero:
ΔSuniverse=ΔSsystem+ΔSsurrounding=0
Thus,
ΔSsurrounding=−ΔSsystem=−9.21J/(K⋅mol)
Step 4: Calculate the Heat Transfer (Q_system)
For an isothermal process, the heat transfer can be calculated using:
Qsystem=T⋅ΔSsystem
Substituting the values:
Qsystem=300⋅9.21
Calculating:
Qsystem=2763J/mol
Step 5: Summary of Results
- ΔSsystem≈9.21J/(K⋅mol)
- ΔSsurrounding≈−9.21J/(K⋅mol)
- Qsystem≈2763J/mol
- ΔSuniverse=0
Conclusion
The correct options based on the calculations are:
- Option A: Qsystem=2763J/mol
- Option C: ΔSsystem=9.21J/(K⋅mol)
- Option D: ΔSsurrounding=−9.21J/(K⋅mol)
- Number of moles (n) = 1 mol
- Initial temperature (T) = 27°C = 300 K (since K = °C + 273)
- Volume is tripled, so if the initial volume is V, the final volume is 3V.
- Given R = 25/3 J/(mol·K)
- Given log(3) = 0.48
The formula for the change in entropy for an isothermal process is:
ΔSsystem=nRln(VfinalVinitial)
Substituting the values:
ΔSsystem=1⋅253⋅2.303⋅log(3)
Calculating:
ΔSsystem=1⋅253⋅2.303⋅0.48
ΔSsystem=25⋅2.303⋅0.483
ΔSsystem≈9.21J/(K⋅mol)
For a reversible process, the total change in entropy of the universe is zero:
ΔSuniverse=ΔSsystem+ΔSsurrounding=0
Thus,
ΔSsurrounding=−ΔSsystem=−9.21J/(K⋅mol)
For an isothermal process, the heat transfer can be calculated using:
Qsystem=T⋅ΔSsystem
Substituting the values:
Qsystem=300⋅9.21
Calculating:
Qsystem=2763J/mol
- ΔSsystem≈9.21J/(K⋅mol)
- ΔSsurrounding≈−9.21J/(K⋅mol)
- Qsystem≈2763J/mol
- ΔSuniverse=0
The correct options based on the calculations are:
- Option A: Qsystem=2763J/mol
- Option C: ΔSsystem=9.21J/(K⋅mol)
- Option D: ΔSsurrounding=−9.21J/(K⋅mol)
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - Chemistry
701 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PT-01
30 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - III CHEMISTRY
46 Videos
- SURFACE CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - Section - 5
1 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
Knowledge Check
1 mole of gas expands isothermally at 37∘C. The amount of heat is absorbed by it until its volume doubled is (R=8.31Jmol−1K−1)
Aa. 411.25 calBb. 418.50 calCc. 420.25 calDd. 425.40 cal
1mol of an ideal gas is allowed to expand isothermally at 27∘C untill its volume is tripled. Calculated DelyasysS and ΔunivS under the following conditions:
a. The expansion is carried out reversibly.
b. The expansion is a free expansion.
View SolutionFor an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using expression =−nRTln.VfVi. A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversible to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively. Choose the correct option
View SolutionOne mole of an ideal gas at 27∘C expanded isothermally from an initial volume of 1 litre to 10 litre. The ΔU for this process is : (R=2calK−1mol−1)
View SolutionIt is known fact that gases expand to fill all available volume and their final pressure becomes equal at every point in connected systeam.
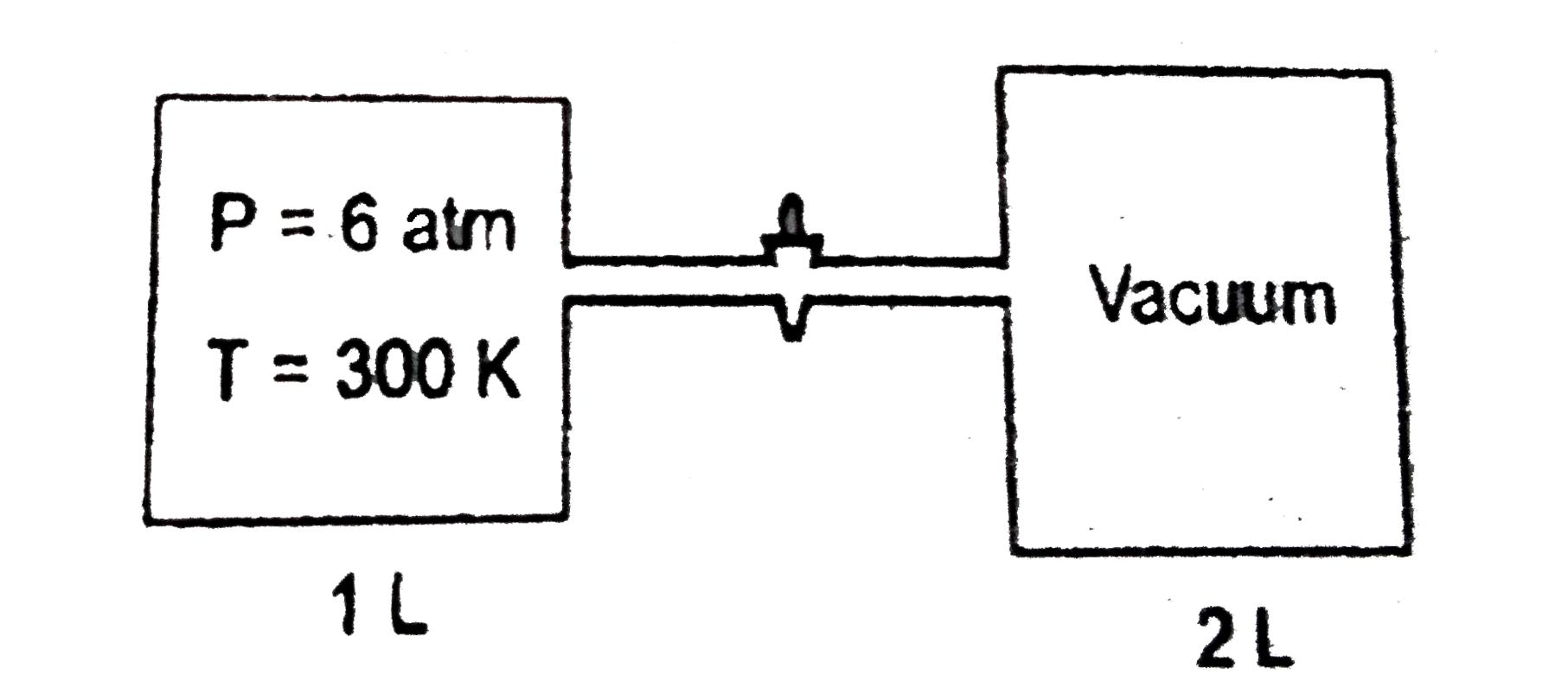
If the gas in the above part weigh 15.36g, then select the correct statement(s) :
(R=112l.atm/mol.K)
View SolutionAn ideal gas is allowed to expand against a constant pressure of 2 bar from 10L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case ?
(Give that, 1 L bar = 100 J)
View SolutionTwo moles of helium gas expanded isothermally and irreversibly at 27∘C from volume 1dm3 to 1m3 at constant pressure of 100 k Pa. Calculate the work done.
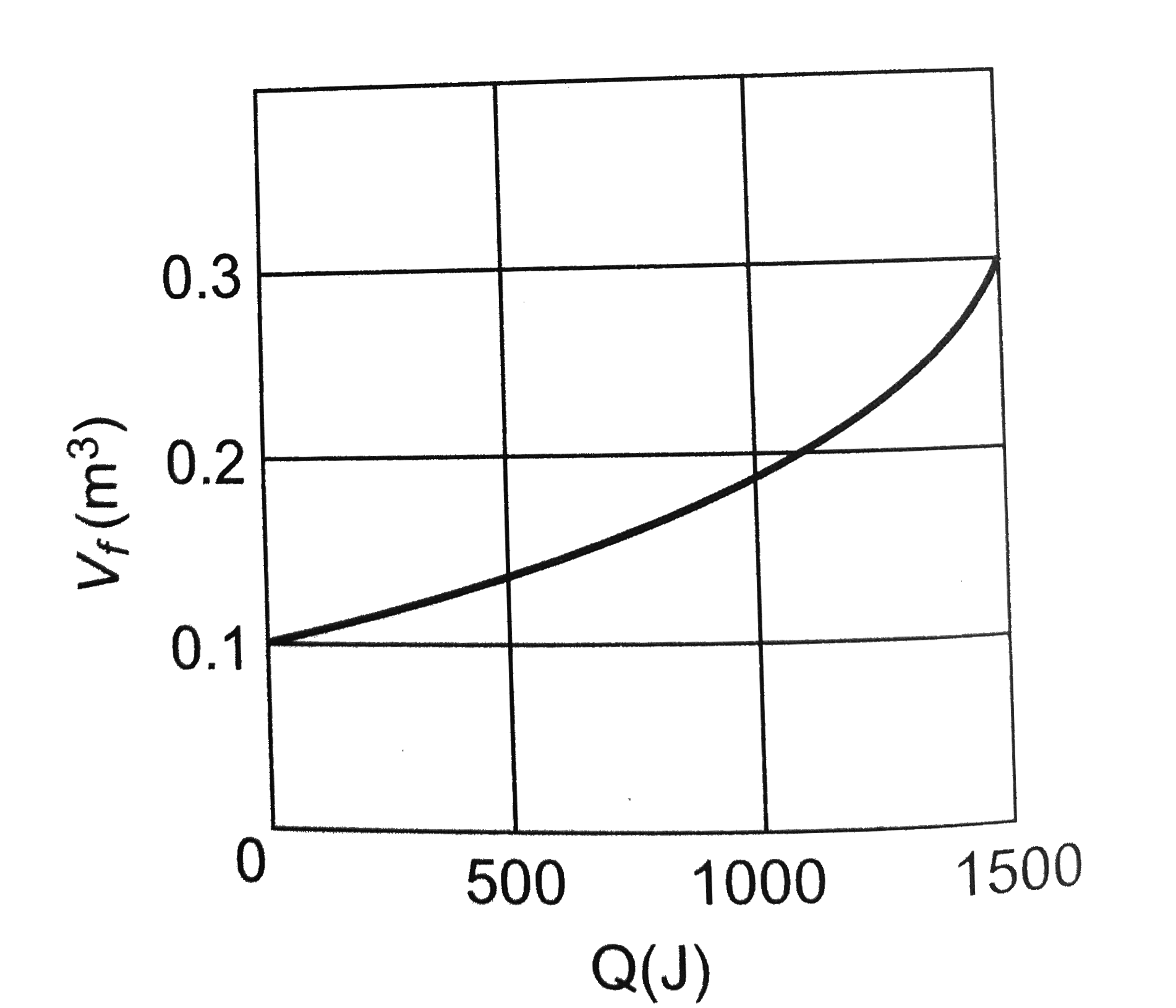
View SolutionSuppose 0.5 moles of an ideal gas undergoes an isothermal expansion as energy is added to it as heat Q. graph shows the final volume Vf versus Q. the temperature of the gas is (useIn9=2andR=253J/mol−K)
View Solution
