In previous question discuss the case when body move downward, upwards and remains at same position when we increases temperature.
To solve the problem regarding the behavior of a body submerged in a fluid when the temperature is increased, we will analyze three cases: when the body moves downward, moves upward, and remains at the same position.
1. Understanding the Variables:
- Let V0 be the original volume of the body.
- Let V1 be the volume of the body submerged at temperature θ1.
- Let V2 be the volume of the body submerged at temperature θ2.
- Let ρf be the density of the fluid and ρs be the density of the solid body.
- The fraction of the volume submerged is given by F=VV0.
2. Setting Up the Equilibrium Condition:
- For equilibrium at temperature θ1:
Weight of the body=Buoyant force
mg=V1ρfg
Simplifying, we get:
V1ρf=m
3. Considering the Change in Temperature:
- When the temperature increases from θ1 to θ2, the volume of the fluid and the body will change due to thermal expansion.
- The new volume of the body at temperature θ2 can be expressed as:
V2=V0(1+3αsΔθ)
- Where Δθ=θ2−θ1 and αs is the coefficient of linear expansion of the solid.
4. New Equilibrium Condition:
- At temperature θ2:
mg=V2ρfg
Thus, we have:
V2ρf=m
5. Analyzing the Three Cases:
- Case 1: Body Moves Downward:
- This occurs when the buoyant force at θ2 is greater than at θ1:
F2>F1⟹V2ρf>V1ρf
- Therefore, if ρf increases (due to thermal expansion), the body moves downward.
- Case 2: Body Moves Upward:
- This occurs when the buoyant force at θ2 is less than at θ1:
F2<F1⟹V2ρf<V1ρf
- Thus, if the fluid contracts more than the body expands, the body moves upward.
- Case 3: Body Remains at Same Position:
- This occurs when the buoyant forces are equal:
F2=F1⟹V2ρf=V1ρf
- This condition can be expressed as:
ρf=3αsΔθ
Conclusion:
From the analysis, we can conclude that the movement of the body in the fluid depends on the relationship between the buoyant forces at different temperatures, which are influenced by thermal expansion properties of both the body and the fluid.
- Let V0 be the original volume of the body.
- Let V1 be the volume of the body submerged at temperature θ1.
- Let V2 be the volume of the body submerged at temperature θ2.
- Let ρf be the density of the fluid and ρs be the density of the solid body.
- The fraction of the volume submerged is given by F=VV0.
- For equilibrium at temperature θ1:
Weight of the body=Buoyant force
mg=V1ρfg
Simplifying, we get:
V1ρf=m
- When the temperature increases from θ1 to θ2, the volume of the fluid and the body will change due to thermal expansion.
- The new volume of the body at temperature θ2 can be expressed as:
V2=V0(1+3αsΔθ)
- Where Δθ=θ2−θ1 and αs is the coefficient of linear expansion of the solid.
- At temperature θ2:
mg=V2ρfg
Thus, we have:
V2ρf=m
- Case 1: Body Moves Downward:
- This occurs when the buoyant force at θ2 is greater than at θ1:
F2>F1⟹V2ρf>V1ρf
- Therefore, if ρf increases (due to thermal expansion), the body moves downward.
- This occurs when the buoyant force at θ2 is less than at θ1:
F2<F1⟹V2ρf<V1ρf
- Thus, if the fluid contracts more than the body expands, the body moves upward.
- This occurs when the buoyant forces are equal:
F2=F1⟹V2ρf=V1ρf
- This condition can be expressed as:
ρf=3αsΔθ
From the analysis, we can conclude that the movement of the body in the fluid depends on the relationship between the buoyant forces at different temperatures, which are influenced by thermal expansion properties of both the body and the fluid.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Solved miscellaneous problems1videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Problem26videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRY AND THERMAL EXPANSIONEXERCISE - Advanced Level Problems13videos
CALORIMETRY AND THERMAL EXPANSION
- BOOK - RESONANCE ENGLISHCHAPTER - CALORIMETRYEXERCISE - Exercise19videos
CALORIMETRY
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITOREXERCISE - Exercise45videos
CAPACITOR
Similar Questions
Knowledge Check
- Question 1 - Select One
When mass and speed of a body is doubled the kinetic energy increases
A2 timesB4 timesC8 timesD16 times
Desert lizards bask in the sun when their body temperature drops below the comfort zone, but move into shade when the ambient temperature starts increasing. This is an example of
View SolutionA helicopter of mass M is lowering a truck of mass m onto the deck of a ship. In first case the helicopter and the truck move downward together (the length of the cable remaine constant). Tension in the cable is T1 when their downward speed is decreasing at a rate of (g)/(10). In second case when the truck gets close to the deck, the helicopter stops moving downward. While it hovers stationary, it lets out the cabel so that the truck is still moving downward. If the truck is moving downward with a speed decreasing at rate of g10, tension in string is now T2, What is ratio T1/T2
View SolutionA body falling vertically .downwards explodes into two equal fragments when it is at a height of 200 m and has a downward velocity of ,6 just after the explosion one pf the fragments is seen to move .downward with a velocity of 8ms−1 .Calculate the position of the centre of mass of the system 5 s after ,the explosion.
View SolutionThe following figure shows a block of mass m suspended from a fixed point by means of a vertical spring. The block is oscillatting simple harmonically and carries a charge q. There also exists a uniform electric field in the region. Consider four different cases. The electric field is zero in case 1, mg/q downward in case 2, mg/q upward in case 3, and 2mg/q downward in case 4. The speed at mean position is same in all cases. Select the correct alternative (s).
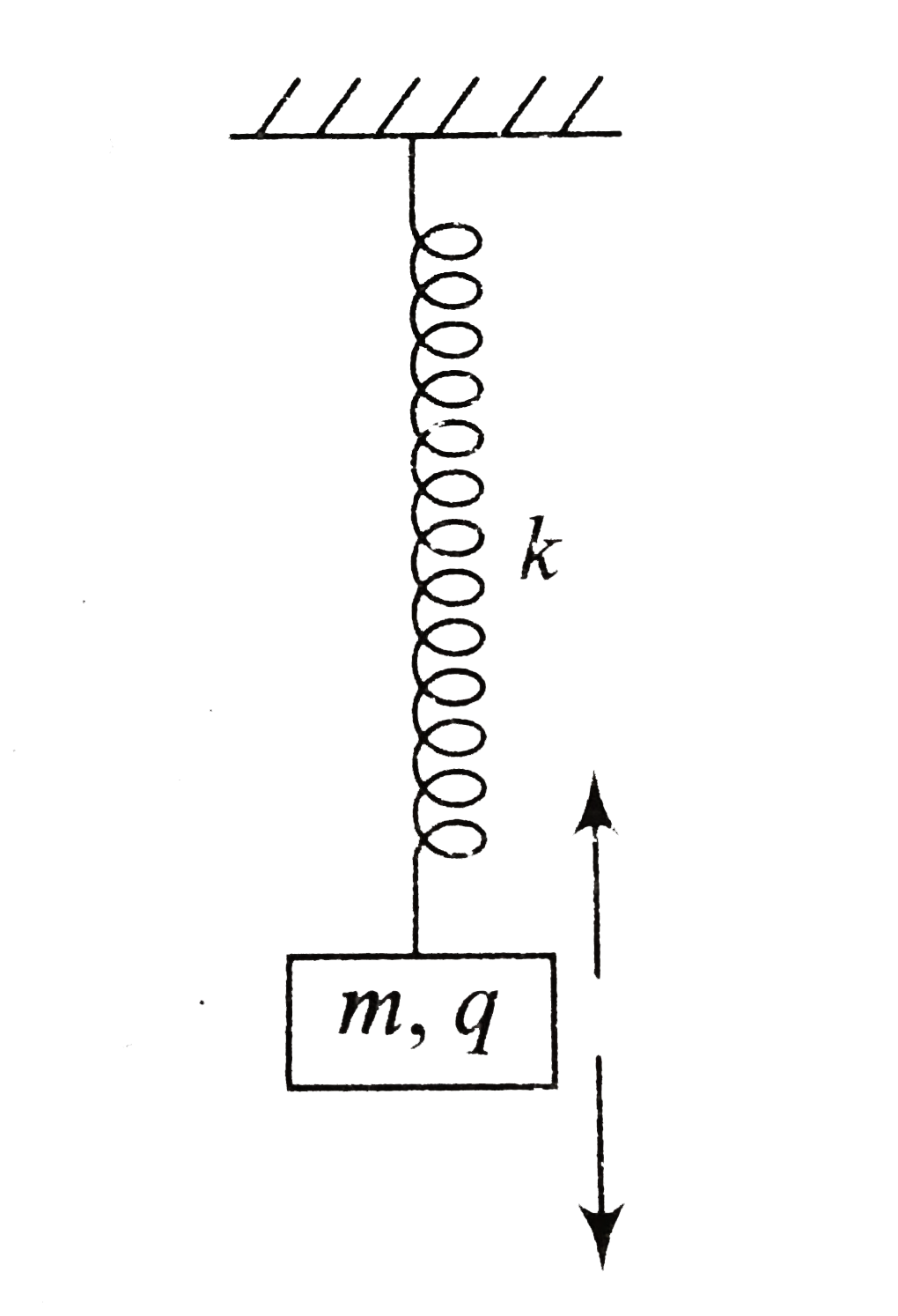 View Solution
View SolutionWhen the temperature of a body increases
View SolutionWhen a body moves with a constant speed along a circle
View SolutionWhen we place a gas cylinder on a van and the van moves, does the kinetic energy of the molecules increase? Does the temperature increase?
View Solution

