In example 3,K1=0.125W/m−.∘C,K2=5K1=0.625W/m−.∘C and thermal conductivity of the unknown material is K=0.25W/m∘CL1=4cm,L2=5L1=20cm. If the house consists of a single room of total wall area of 100m2. then find the power of the electric heater being used in the room.
Is–tmethod––––––––––––R1=R2=(4×10−2m)(0.125w/m−∘C)(100m2)=32×10−4.∘C/w
∴25−20R1=20−T3R
R=LKA=112×10−4.∘C/W
the equivalent thermal resistance of the entire wall =R1+R2+2R=288×10−4.∘C/W
∴ Net heat current i.e. amount of heat flowing out of the house per second =TH−TCR
=25∘C−(−20∘C)288×104.∘C/w=45×104288watt
=1.56Kwatt
Hence the heater must supply 1.56kW to compenstate for the outflow of heat.
IIn––dmethod–––––––––––––
i=T1−T2R1=25−2032×10−4=1.56Kwatt
Topper's Solved these Questions
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Board Level Exercise
14 Videos
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Exercise-1
1 Videos
- HEAT TRANSFERBOOK - RESONANCE ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - Advancel Level Problems
17 Videos
- GRAVITATIONBOOK - RESONANCE ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise
21 Videos
- KINEMATICSBOOK - RESONANCE ENGLISHCHAPTER - KINEMATICSEXERCISE - Exercise
65 Videos
Similar Questions
The molar conductivity of 0.05 M BaCl2 solution at 25∘C is 223Ω−1cm2mol−1. What is its conductivity?
View SolutionFigure shows in cross section a wall consisting of four layers with thermal conductivities K1=0.06W/mK,K3=0.04W/mKandK4=0.10W/mK. The layer thickness are L1=1.5cm,L3=2.8cmandL4=3.5cm. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer 3and4 is:

View Solution
Knowledge Check
Figure shows in cross section a wall consisting of four layers with thermal conductivities K1=0.06W/mK,K3=0.04W/mKandK4=0.10W/mK. The layer thickness are L1=1.5cm,L3=2.8cmandL4=3.5cm. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer 3and4 is:
 A−1∘CB−3∘CC2∘CD0∘C
A−1∘CB−3∘CC2∘CD0∘CIf layer thickness L2 is 1.4cm, then its thermal conductivity K2 will have value (in W/mK)
A2×10−2B2×10−3C4×10−2D4×10−3
Figure shows in cross section a wall consisting of four layers with thermal conductivities K1=0.06W/mK,K3=0.04W/mKandK4=0.10W/mK. The layer thickness are L1=1.5cm,L3=2.8cmandL4=3.5cm. The temperature of interfaces is as shown in figure. energy transfer through the wall is in steady state. the temperature of the interface between layer 3and4 is:

View SolutionThe molar conductivity of 0.05 M BaCl2 solution at 25∘C is 223Ω−1cm2mol−1. What is its conductivity?
View SolutionThe thermal conductivity of brick is 1.7Wm−1K−1, and that of cement is 2.9Wm−1K−1.What thickness of cement will have same insulation as the brick of thickness 20cm.
View SolutionThe thermal conductivity of brick is 1.7Wm−1K−1, and that of cement is 2.9Wm−1K−1.What thickness of cement will have same insulation as the brick of thickness 20cm.
View SolutionFigure shows the cross section of a wall made of three layers. The layer thicknesses are L1,L2=0.750L1, and L3=0.350L1. The thermal conductivities are k1,k2=0.900k1, and k3=0.800k1. The temperature at the left side and right side of the wall are TH=30.0∘C and TC=−15.0∘C, respectively. Thermal conduction is steady . (a) What is the temperature difference ΔT2 across layer 2 ( between the left and right sides of the layer ) ? If k2 were, instead, equal to 1.1k1, (b) would the reate at which energy is conducted through the wall be greater than, less than, or the same as proviously, and (c ) what would be the value of ΔT2 ?
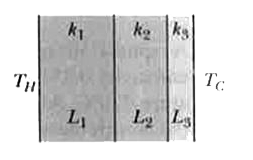
View SolutionIf the length (l) (in m) and width (w) (in m) of a room are related by the expresion w=12l+1, then the width of the room is
View Solution
