A string of length 1.5 m with its two ends clamped is vibrating in fundamental mode Amplitude at the centre of the string is 4 mm. Distance between the two points having amplitude 2mm is
1m
75cm
60cm
50cm
The correct Answer is:A
λ=2l=3m
Equation of standing wave
y=2Asinkxcosωt
y=A as amplitude is 2A
A=2Asinkx
2πλx=π6
⇒x1=14m
and 2πλ.x=5π6
⇒x2=1.25m
⇒x2−x1=1m
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 836videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 845videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 814videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View SolutionA string of length 1.5 m with its two ends clamped is vibrating in fundamental mode. Amplitude at the centre of the string is 4 mm. Minimum distance between the two points having amplitude 2 mm is:
View Solution
Knowledge Check
- Question 1 - Select One
A string of length 2 m is fixed at both ends. If this string vibrates in its fourth normal mode with a frequency of 500 Hz, then the waves would travel on its with a velocity of
A125 ms−1B250 ms−1C500 ms−1D1000 ms−1
A string of mass per unit length μ is clamped at both ends such that one end of the string is at x=0 and the other is at x=L. When string vibrates in fundamental mode, amplitude of the midpoint of string is a and tension in the string is F. Find the total oscillation energy (in J) stored in the string. (Use L=1 m, F = 10N, a = 1/pi m).
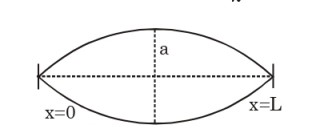 View Solution
View SolutionA string of mass 'm' and length l, fixed at both ends is vibrating in its fundamental mode. The maximum amplitude is 'a' and the tension in the string is 'T'. If the energy of vibrations of the string is π2a2TηL. Find η
View SolutionA string of length l is fixed at both ends and is vibrating in second harmonic. The amplitude at anti-node is 5 mm. The amplitude of a particle at distance l/8 from the fixed end is
View SolutionA uniform string is clamped at x=0 and x = L and is vibrating in its fundamental mode. Mass per unit length of the string is μ, tension in it is T and the maximum displacement of its midpoint is A. Find the total energy stored in the string. Assume to be small so that changes in tension and length of the string can be ignored
View SolutionA string of length 'L' is fixed at both ends . It is vibrating in its 3rd overtone with maximum amplitude 'a'. The amplitude at a distance L/3 from one end is
View SolutionTwo strings of the same length but different mass per unit length are used to suspend a rod whose density varies as ρ=ρ0[1+αx] as shown in the figure. The frequency of standing waves produced in the string is in the ratio n:1, when both the strings are vibrating in their fundamental mode. If the mass per unit length of string (l) is μ0, calculate the mass per unit length of the other string.
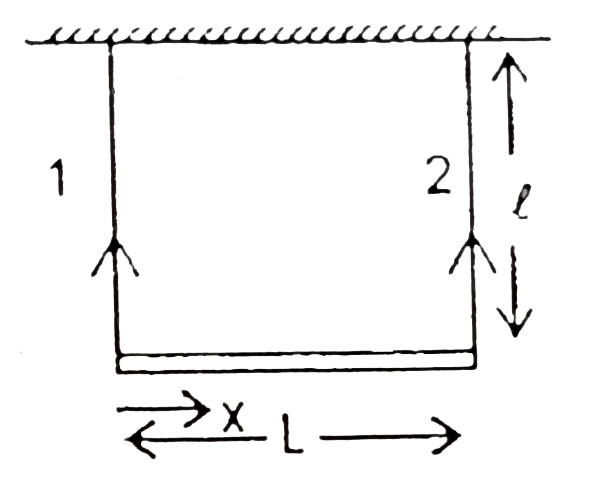 View Solution
View SolutionA string clamped at both ends vibrates in its fundamental mode. Is there any position (except the ends) on the string which can be touched without disturbing the motion ? What if the string vibrates in its first overtone ?
View Solution

