_S01_038_Q01.png)
As per the shown figure the central solid cylinder starts with initial angular velocity ω0 Find the time after which the angular velocity becomes half.
The correct Answer is:t=m(R2−R1)/ln24πηlnaR1
F=ηAdvdz, where dvdz=ωR1−0R2−R1
F=η2πR1lωR1R1−R1

and τ=FR1=2πηR31ωlR2−R1
I∝2πηR31ωlR2−R1
⇒MR212(−dωdt)=2πηR31ωlR2−R1
or −ω0/2∫ω0dωω=4πηR1lm(R2−R1)t∫0dt
⇒t=m(R2−R1)ln24πηlR1

h=40×10−2100−[η=10−1poise =10−2N−sec−m2]
=4×10−3m=4mm
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 89 illustration
Explore 5 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 90 Illustration
Explore 2 Videos
- DAILY PRACTICE PROBLEMSBook:RESONANCE ENGLISHChapter:DAILY PRACTICE PROBLEMSExercise:dpp 88
Explore 7 Videos
- CURRENT ELECTRICITYBook:RESONANCE ENGLISHChapter:CURRENT ELECTRICITYExercise:Exercise
Explore 53 Videos
- ELASTICITY AND VISCOCITYBook:RESONANCE ENGLISHChapter:ELASTICITY AND VISCOCITYExercise:Advanced Level Problems
Explore 9 Videos
Similar Questions
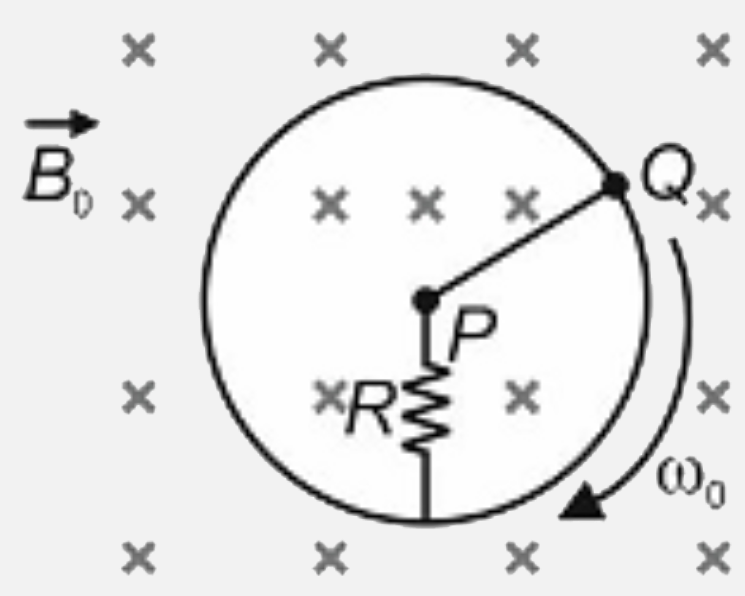
A uniform rod PQ of length I and mass m is placed on a smooth horizontal surface. It is hinged at one of its ends and touches the conducting circular loop at another end. The system is subjected to vertical magnetic field B0. Rod is given angular velocity ω0 about the axis passing through P. If the time after which its angular velocity becomes half is abmRln2B2t2 . Find the value of (a+b), where a and b are smallest positive integers.
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View Solution
Knowledge Check
A mass is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre with a angular velocity ω0. If the length of the string and angular velocity are doubled, the tension in the string which was initially T0 is now
AT0BT0/2C4T0D8T0

The assembly of two discs as shown in figure is placed on a rough horizontal surface and the front disc is given an initial angular velocity ω0. Determine the final linear and angular velocity when both the discs start rolling. it is given that friction is sufficient to sustain rolling the rear wheel from the starting of motion.
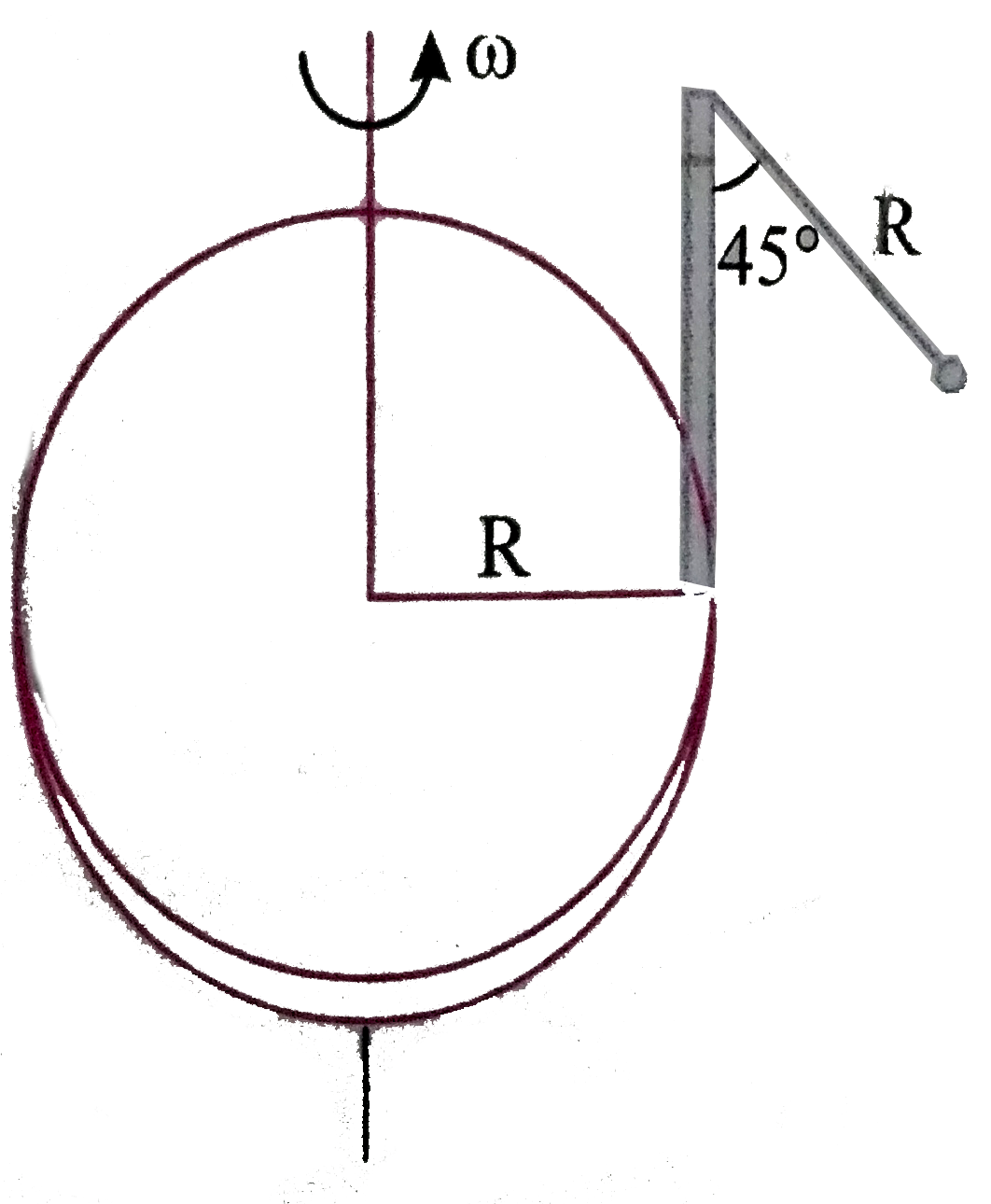
View SolutionA disc of radius R has a light pole fixed perpendicular to the disc at its periphery which in turn has a pendulum of length R attached to its other end as shown in figure. The disc is rotated with a constant angular velocity ω The string is making an angle 45∘ with the rod. Then the angular velocity ω of disc is
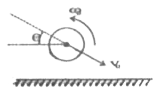
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
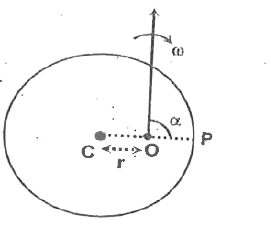
View SolutionRing is fixed on the horizontal surface and a rod starts rotatiing with constant angular velocity ω fixed at O as shown in the figure. Find the magnitude of velocity of intersection points of rod and ring when aplha become 90∘
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA uniform solid sphere of mass M=1 kg and redius R=50 cm is projected with velocity v0=1m/s and simultancously given a reverse spin ω0 as shown in figure. The horizontal surface is rough. What is initial angular velocity ω0 for which rotation and translation stops simultaneously i subsequent motion
View SolutionThe initial angular velocity of a heavy flywheel rotating on its axis is w0. Its angular velocity decreases due to friction. At the end of the first minute its angular velocity is 0.8ω0. What is its angular velocity at the end of third minute, if the frictional force is constant ?
View Solution