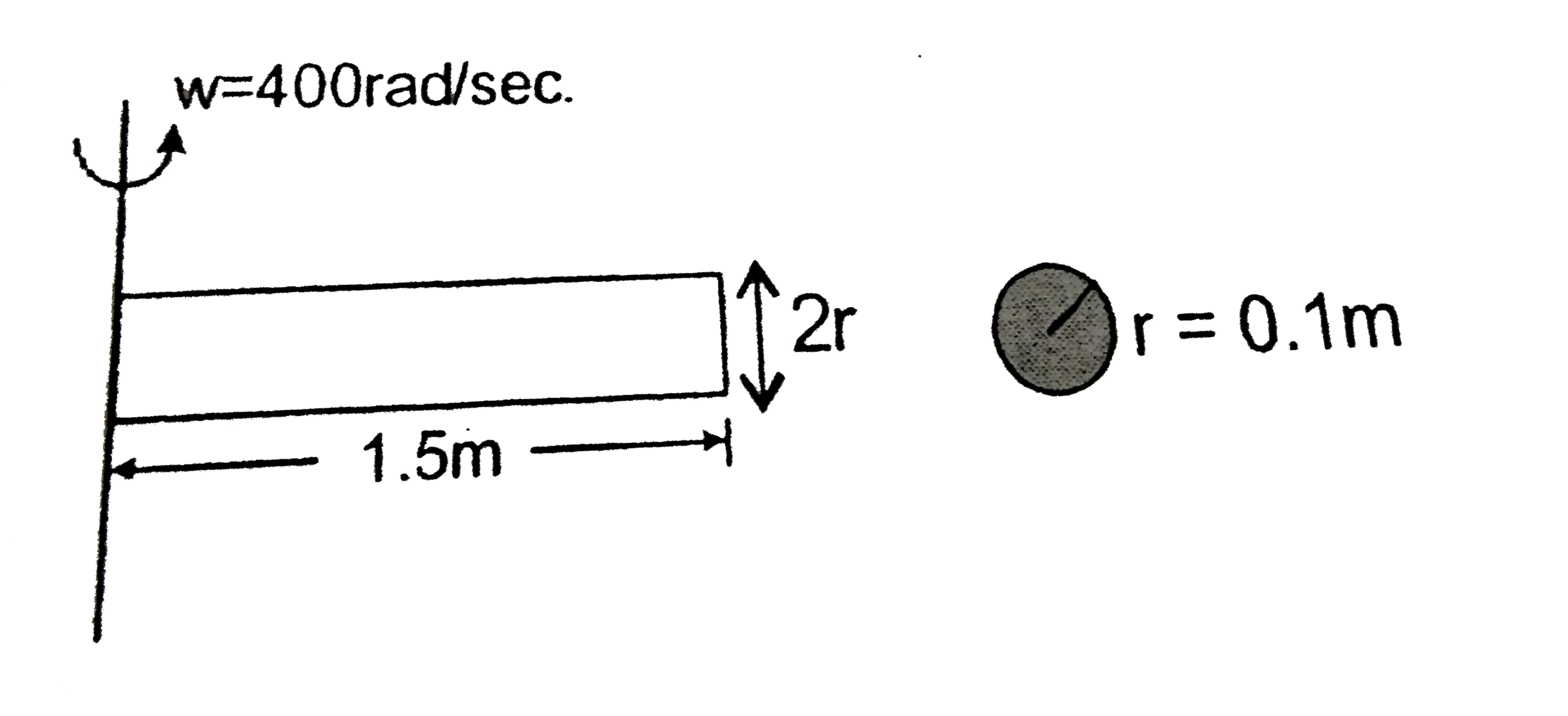
A rod of $1.5 m$ length and uniform density $10^{4} k g / m^{3}$ is rotating at an angular velocity $400 r a d / sec$ about its one end in a horizontal plane. Find out elongation in rod.
Given $y = 2 \times 10^{11} N / m^{2}$

Video Solution

Text Solution

Verified by Experts

mass of shaded portion
$m' - \frac{m}{l} (l - x) [$ where $m =$ total mass $ρ A l]$
$T = m' ω^{2} [\frac{l - x}{2} + x] \Rightarrow T = \frac{m}{l} (l - x) ω^{2} (\frac{l + x}{2}) T = \frac{m ω^{2}}{2 l} (l^{2} - x^{2})$

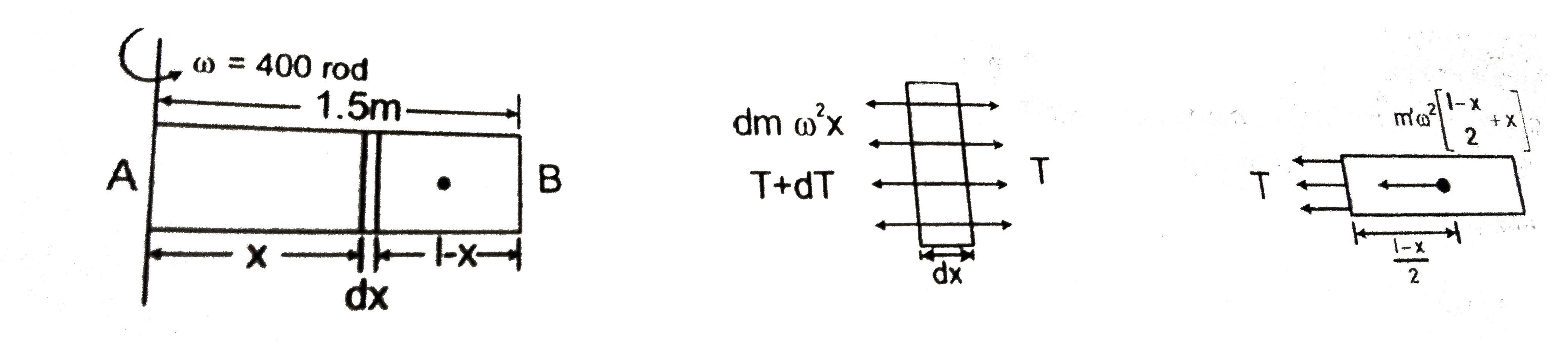
this tension will be maximum at $A (\frac{m ω^{2} l}{2})$ and minum at 'B' (zero), elongation in element of width $d x' = \frac{T d x}{A y}$
Total elongation
$δ = \int \frac{T d x}{A y} = l \int 0 \frac{m ω^{2} (l^{2} - x^{2})}{2 l A y} d x$
$δ = \frac{m ω^{2}}{2 l A y} {[l^{2} x - \frac{x^{3}}{3}]}_{0}^{2} = \frac{m ω^{2} \times 2 l^{3}}{2 l A y \times 3} = \frac{m ω^{2} l^{2}}{3 A y} = \frac{ρ A l ω^{2} l^{2}}{3 A y}$
$δ = \frac{ρ ω^{2} l^{3}}{3 y} = \frac{10^{4} \times (400) \times {(1.5)}^{3}}{3 \times 2 \times 10^{11}} = 9 \times 10^{- 3} m = 9 m m$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-DAILY PRACTICE PROBLEMS-dpp 89 illustration

Home
Ask Doubt
Profile