A ball of mass 'm' drops from a height which sticks to a mass-less hanger after striking it. Neglecting overturning, Find out the maximum extension in rod, assuming that the rod is mass-less.
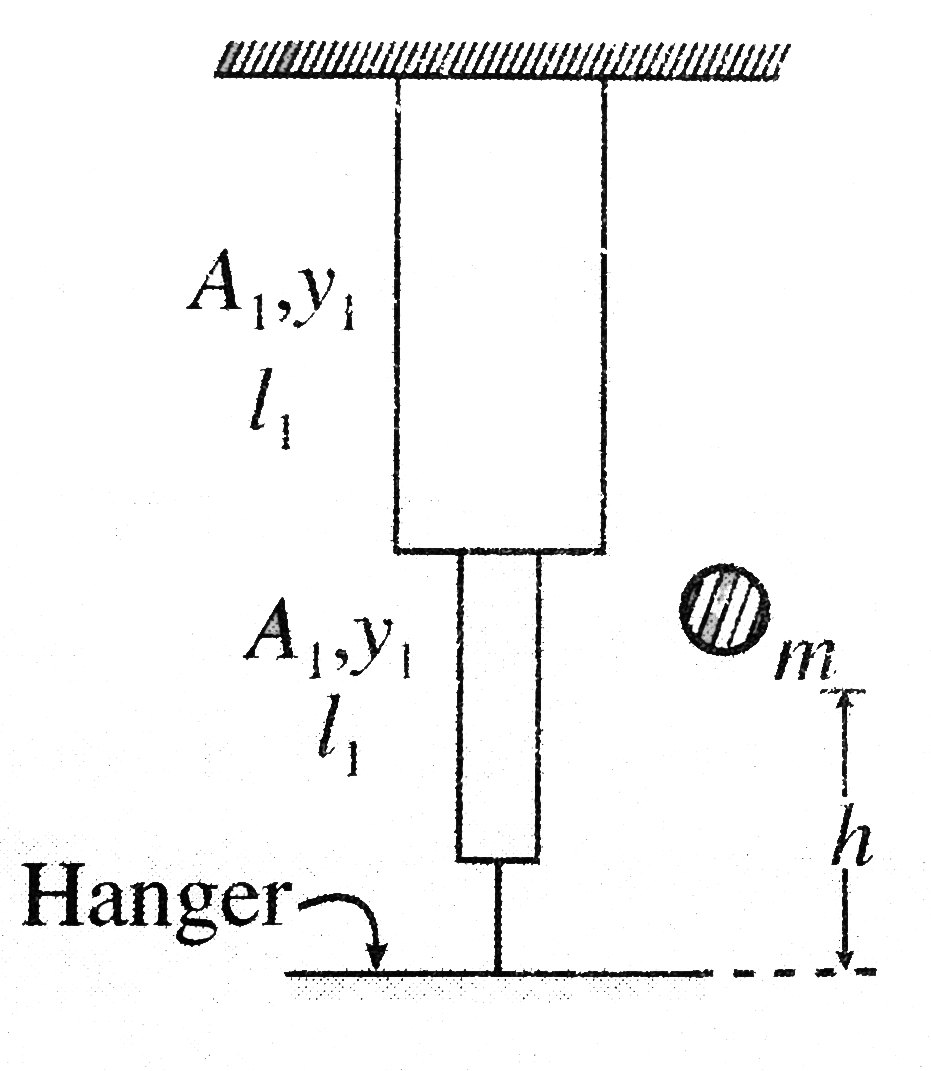
Applying energy conservation
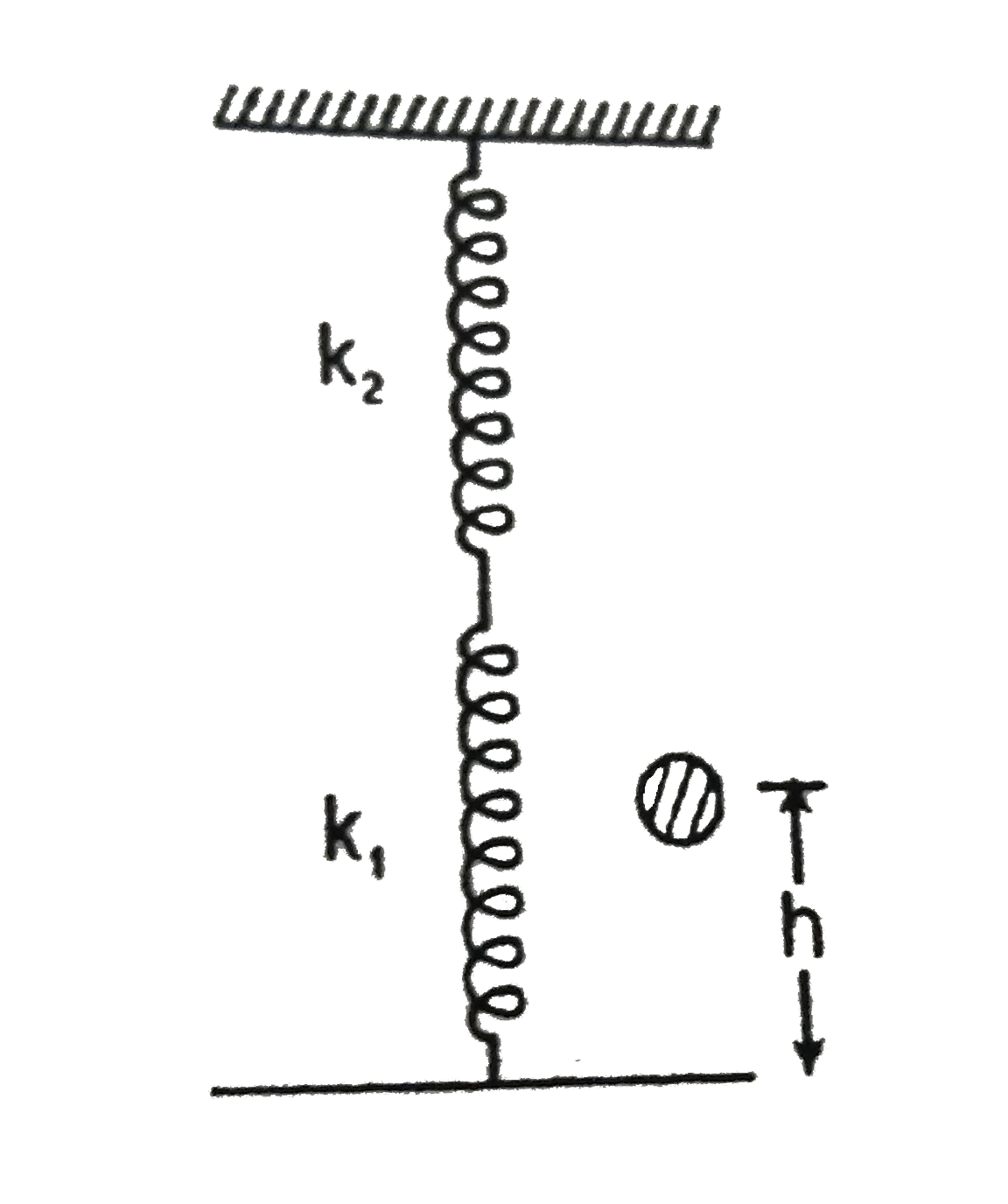
mg(h+x)=12k1k2k1+k2x2
where k1=A1y1l1k2=A2y2l2
&Keq=A1A2y1y2A1y1l2+A2y1l1
keqx2−2mgx−2mgh=0
x=2mg±√4m2g2+8mghkeq2keqxmax=mgkeq+√m2g2k2eq+2mghkeq
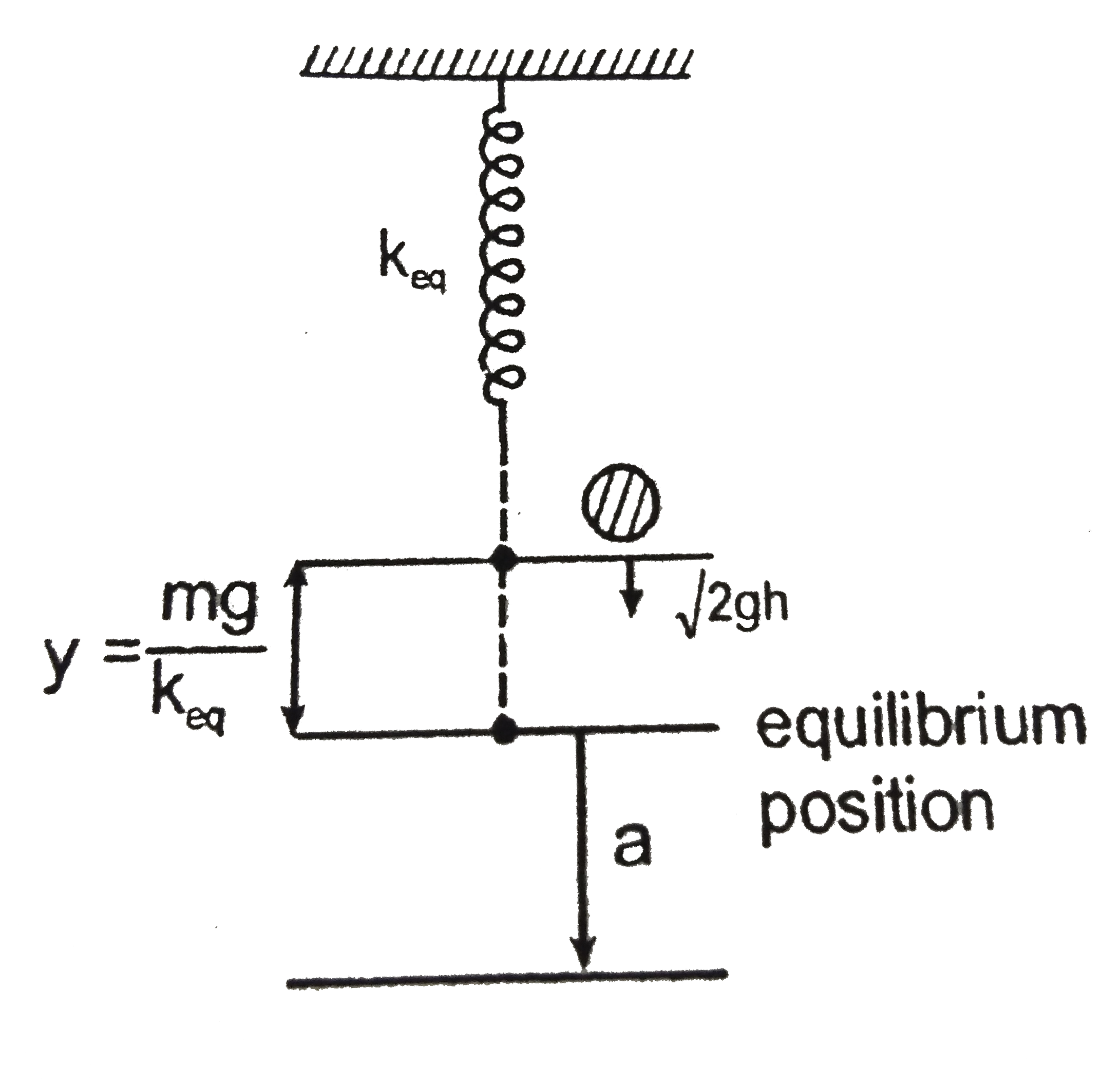
BY S.H.M.
w=√keqmv=ω√a2−y2
√2gh=√keqm√a2−y2⇒√2mghkeq+m2g2k2eq=a
mmax extension a+y=mgkeq+√m2g2keq+2mghkeq
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 91 illustration2videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 92 illustration2videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 89 illustration5videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise53videos
CURRENT ELECTRICITY
- BOOK - RESONANCE ENGLISHCHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
A ball of mass 'm' drops from a height which sticks to a massless hanger after striking it. Neglecting overturning. Find out the maximum extension in rod, assuming that the rod is massless.
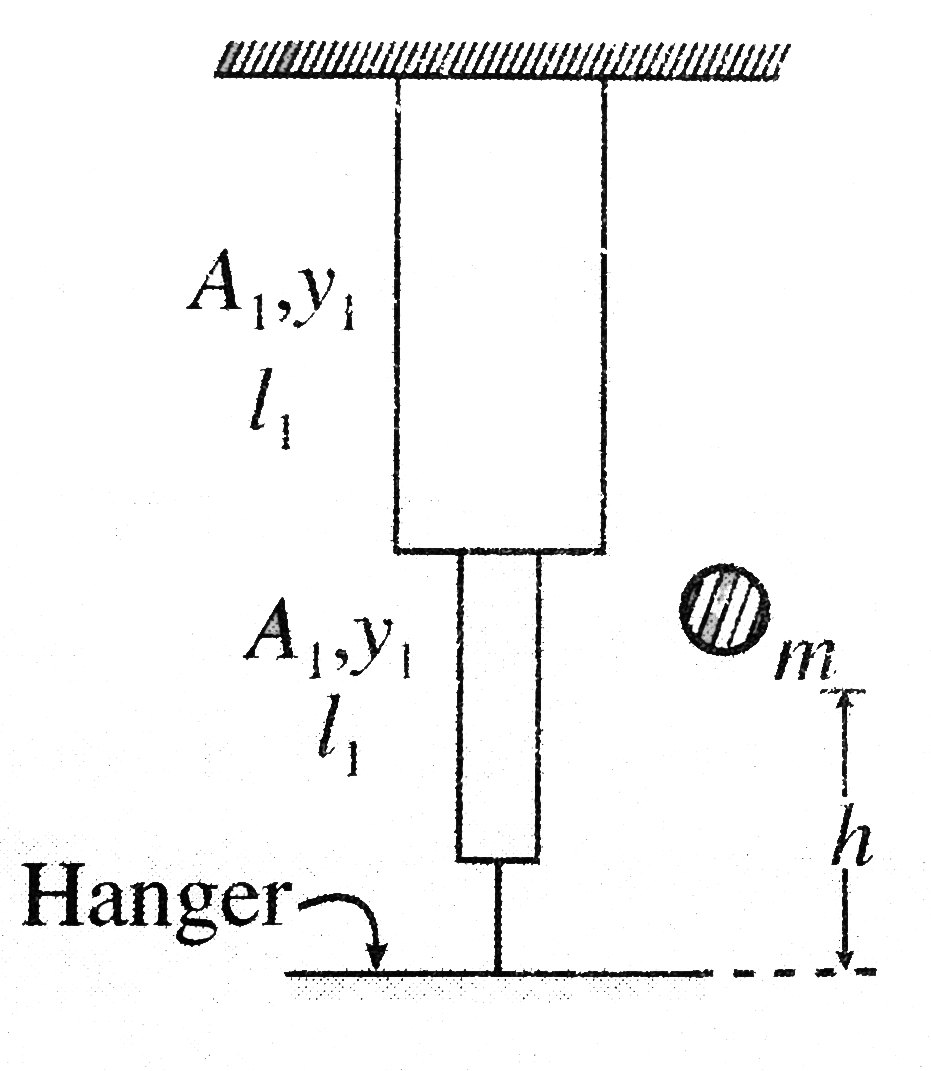 View Solution
View Solution_S01_010_Q01.png)
Hanger is mass less a ball of mass m drops a height h which sticks to hanger after striking. Neglect over turning find out the maximum extension in rod. Assuming or id massless let maximum extension be xmax.View SolutionA mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
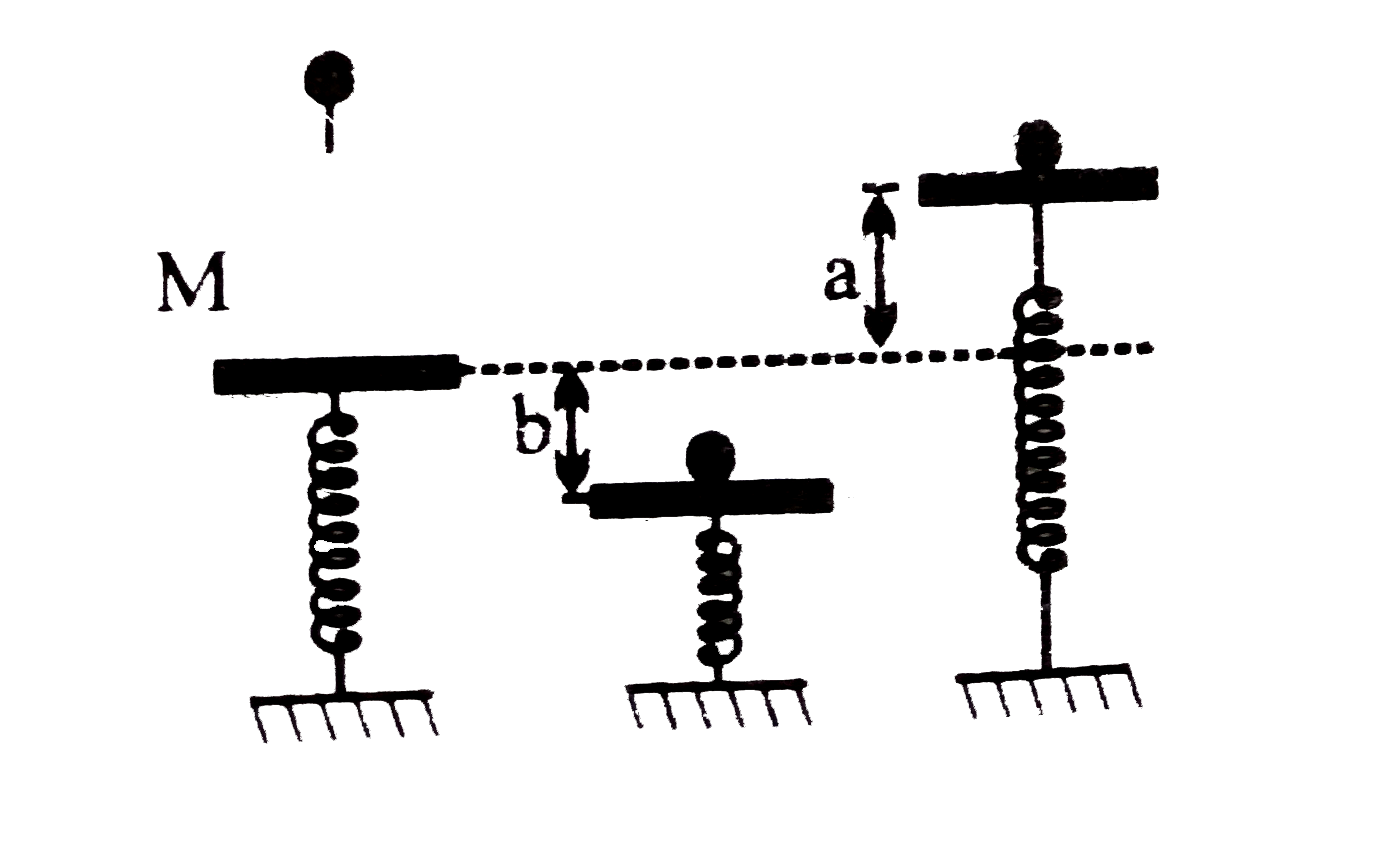
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?View SolutionA mass M is in static equilibrium on a massless vertical spring as shown in the figure. A ball of mass m dropped from certain height sticks to the mass M after colliding with it.
The oscillations they perform reach to height'a' above the original level of scales & depth 'b' below it.
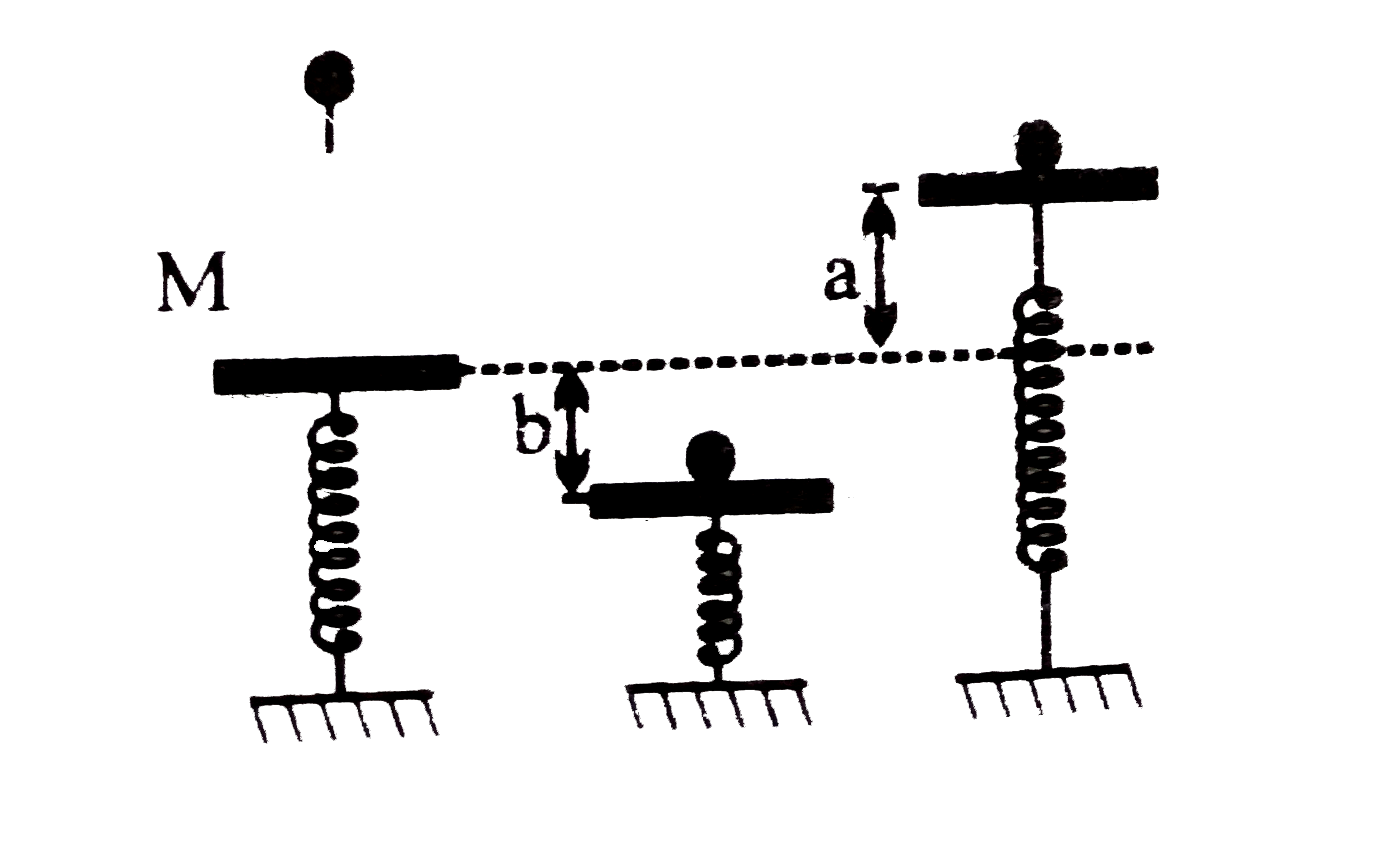
(a) Find the constant of force of the spring.,
(b) Find the oscillation frequency.
(c ) What is the height above the initial level from which the mass m was dropped?View SolutionA ball of mass m is dropped from a height h in a tunnel, made across the earth (mass = M, radius = R) passing through its center. If h<<R such that the motion of the particle through h can be considered uniformly accelerated at g, then the time period of the particle is
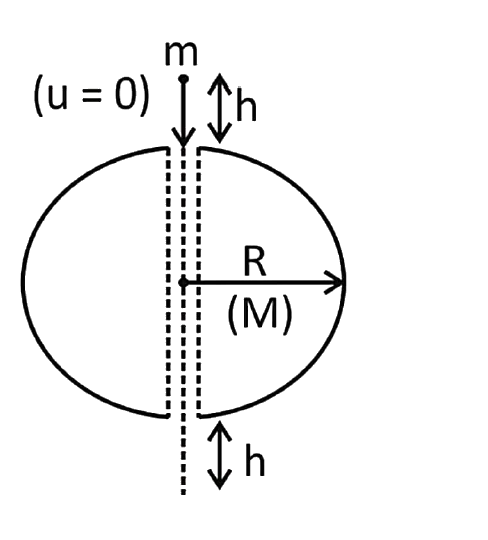 View Solution
View SolutionA ball of mass m is thrown straight up. It goes to a maximum height and then returns. Finally it strikes ground. In the whole process.
View SolutionA ball of mass m when dropped from certain height as shown in diagram, strikes a wedge kept on smooth horizontal surface and move horizontally just after impact. If the ball strikes the ground at a distance d from its initial line of fall, thenthe amplitude of oscillation of wedge after being hit by the ball will be
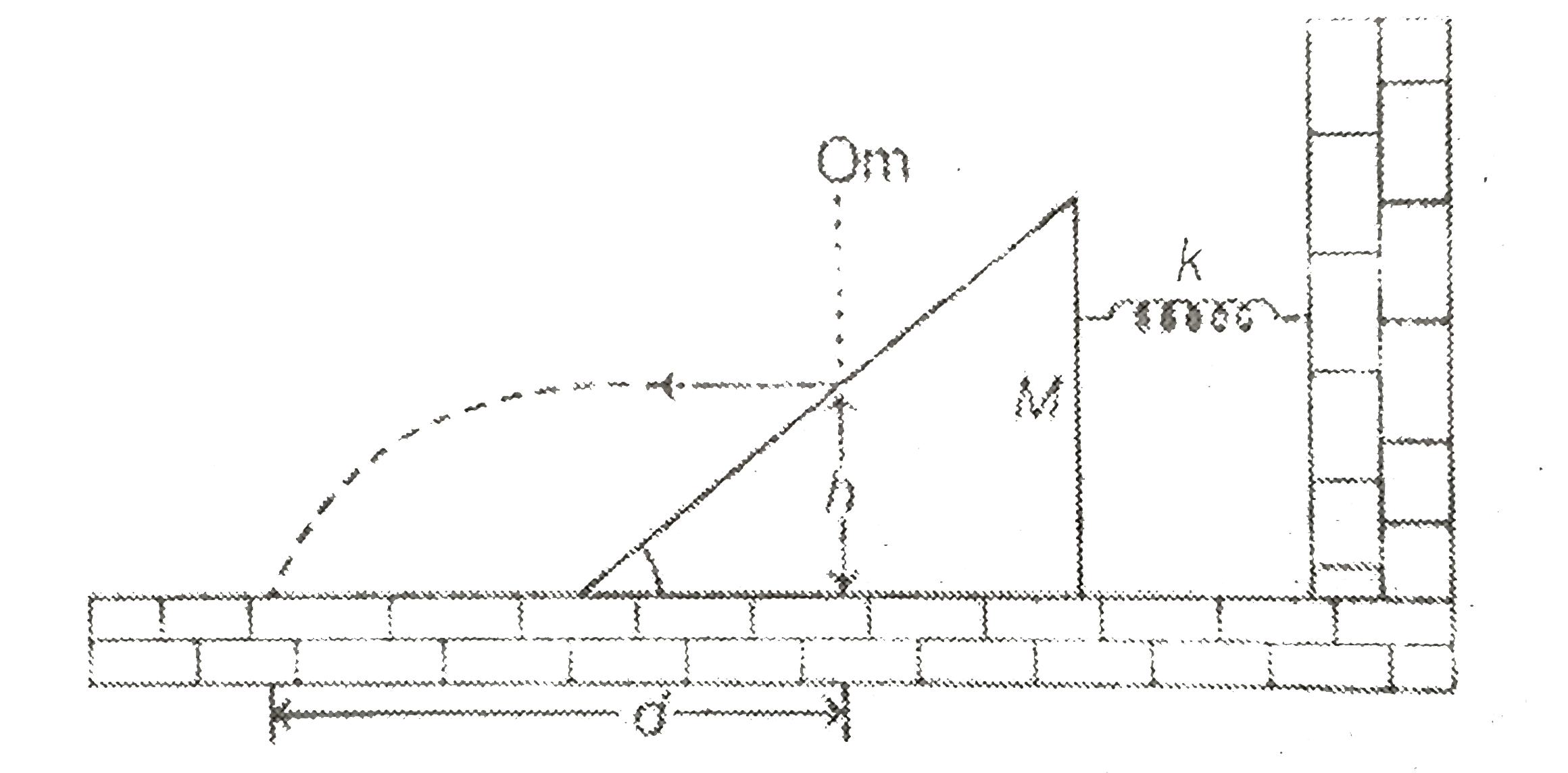 View Solution
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
 View Solution
View SolutionA ball of mass 20 g falls from a height of 10 m and after striking the ground.It rebounds from the ground to a height of 8 m .
(a) Calculate:
(i)The kinetic energy of the ball just before striking the ground ,and
(ii)The loss in kinetic energy of the ball on striking the ground,and
(ii)the loss in kinetic energy of the ball on striking the ground.
(b)What happens to the loss in kinetic energy in part(ii) ?
Take g=10 m s−2 Neglect air friction .View Solution
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.View Solution

