A thin uniform rod of length l and mass m is freely pivoted about its

A thin uniform rod of length $l$ and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)
ocr_image
The minimum impulse J required to bring it to rest :

View Solution

A thin uniform rod of length $l$ and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)
ocr_image
The distance from the pivot at which impulse, must be applied, if there is to be no horizontal force at the pivot

View Solution

A thin uniform rod of length $l$ and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot)
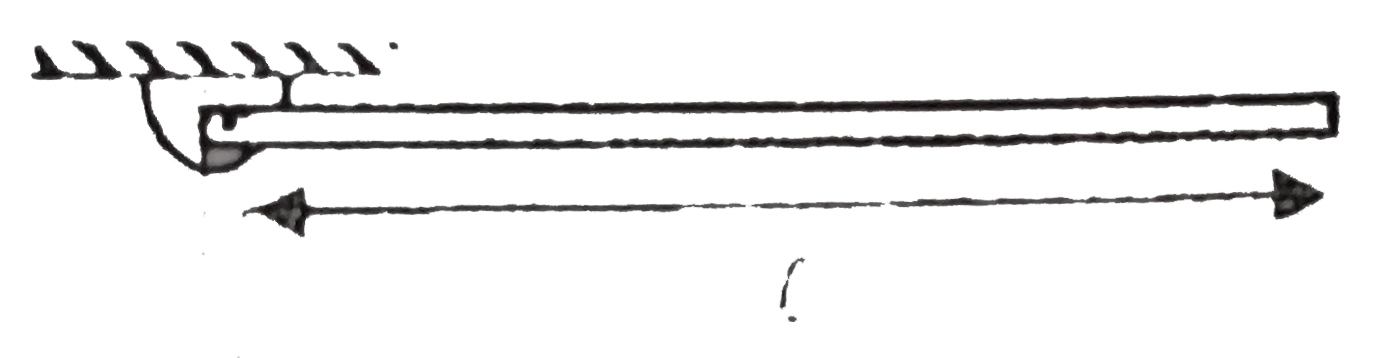
ocr_image
If rod is stopped by applying minimum impulse than what is impulse imparted by pivot

View Solution

A uniform rod of length $l$ and mass $m$ is free to rotate in a vertical plane about $A$ as shown in Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is
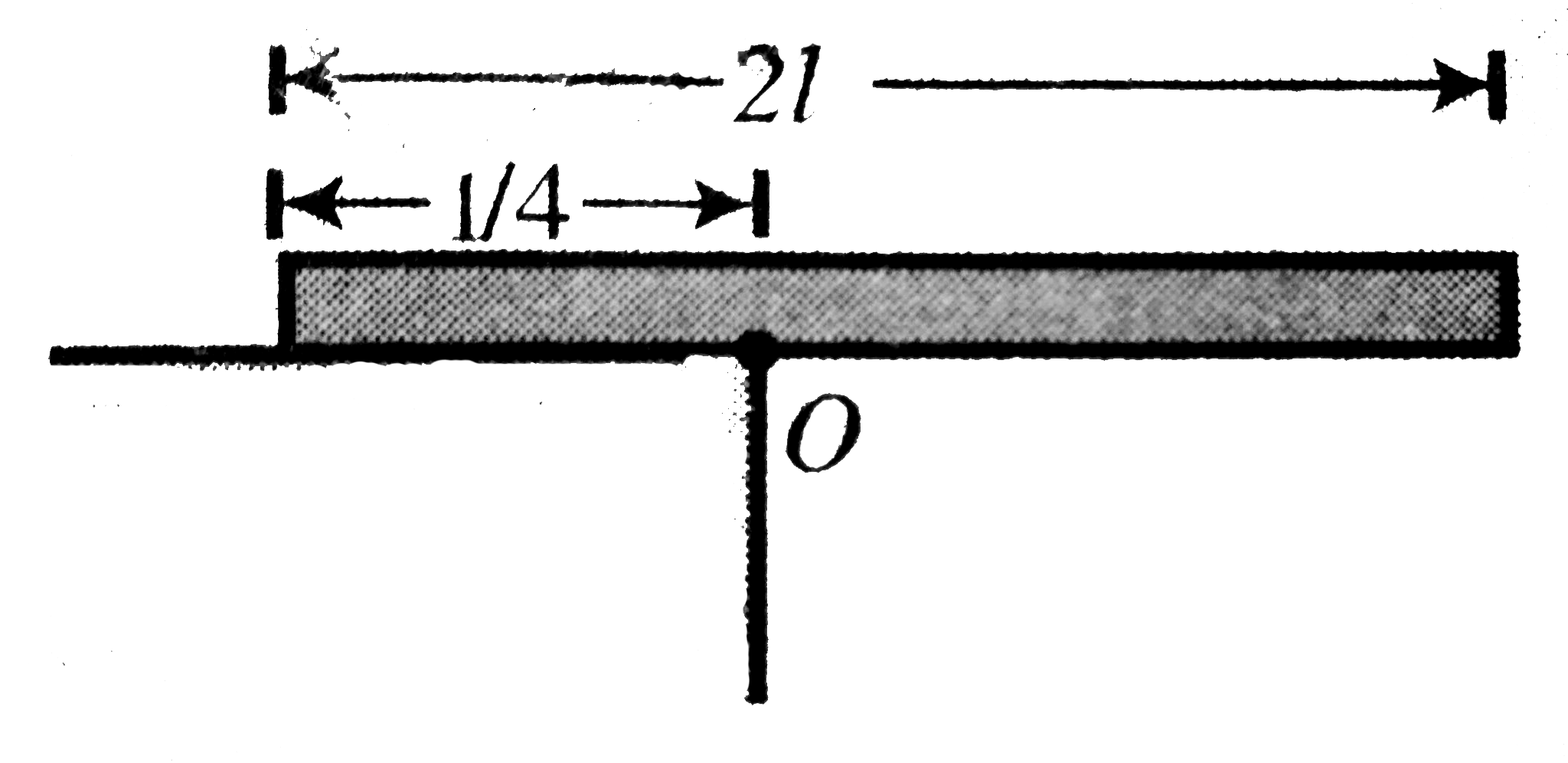
ocr_image

View Solution

One fourth length of a uniform rod of length $2 l$ and mass $m$ is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.
ocr_image

View Solution

A rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is

View Solution

A uniform thin rod of length $l$ and mass $m$ is hinged at a distance $l / 4$ from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
ocr_image

View Solution

A unifrom rod of length $l$ and mass $m$ is free to rotate in a vertical plane about $A$ , Fig. The rod initially in horizontal position is released. The initial angular acceleration of the rod is $(M I of rod about A is \frac{m l^{2}}{3})$
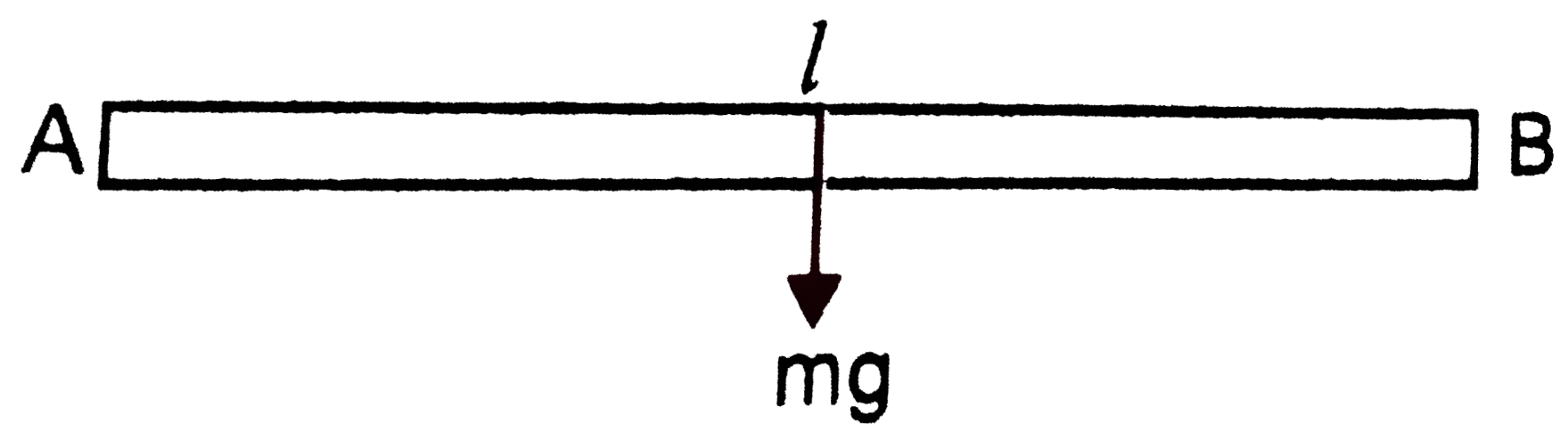
ocr_image

View Solution

A uniform rod AB of length l and mass m is free to rotate about point A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is $\frac{m l^{2}}{3}$ , the initial angular acceleration of the rod will be
ocr_image

View Solution

A thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is

View Solution

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-DAILY PRACTICE PROBLEM-DPP No.67