Figure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
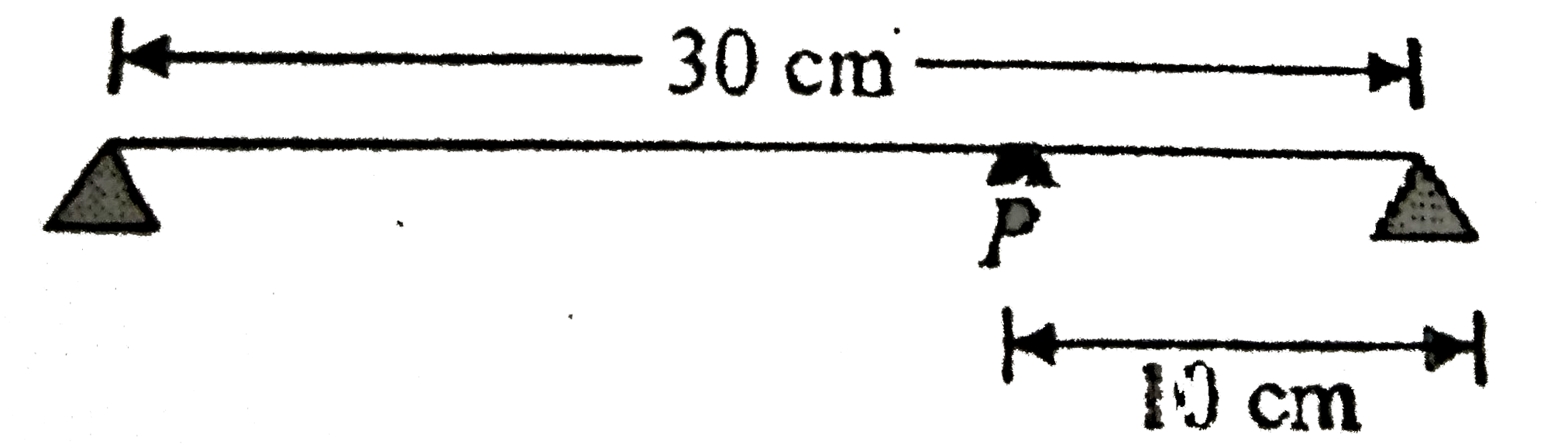
At which of the following frequencies the point P on string will have maximum oscillation amplitude among all points on string :
2003Hz
100Hz
200Hz
None of these
The correct Answer is:D
Wave velocity in string is
V=√Tμ=√400.1=20m/s
Fundamental frequency of string oscillations is
n0=v2e=200.6=1003Hz
Thus string will be in resonance with a turning fork of frequency
nf=1003Hz,2003Hz,100Hz,4003Hz....
Here rider will not oscillate at all only if it is at a node of stationary wave in all other cases of resonance and non-resonance it will vibrate at the frequency of tuning fork. At a distance l3 from one end node will appear at 3rd,6th,9th similar higher Harmonics i.e. at frequencies 100 Hz,200 Hz
If string is divided in odd no of segments these segments can never resonance simultaneously hence at the location of rider antinode is never obtained at any frequency.
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.69
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.70
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCE ENGLISHCHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.67
10 Videos
- CURRENT ELECTRICITYBOOK - RESONANCE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
19 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Figure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
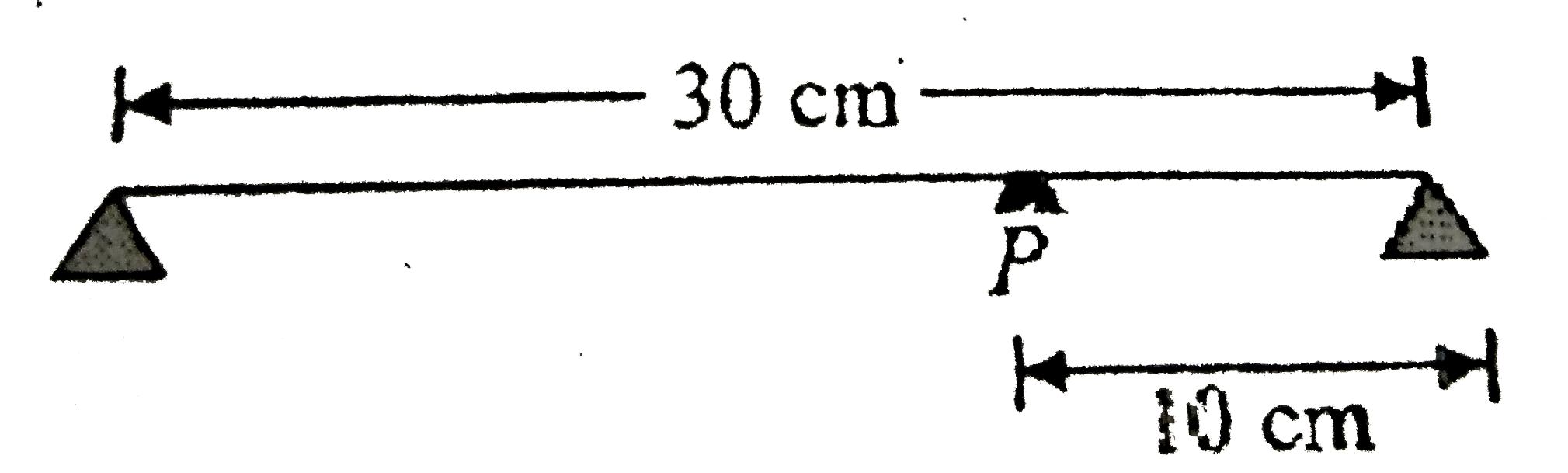
Now if the tension in the string is made 160N, at which of the following frequencies of turning fork , rider will not vibrate at all
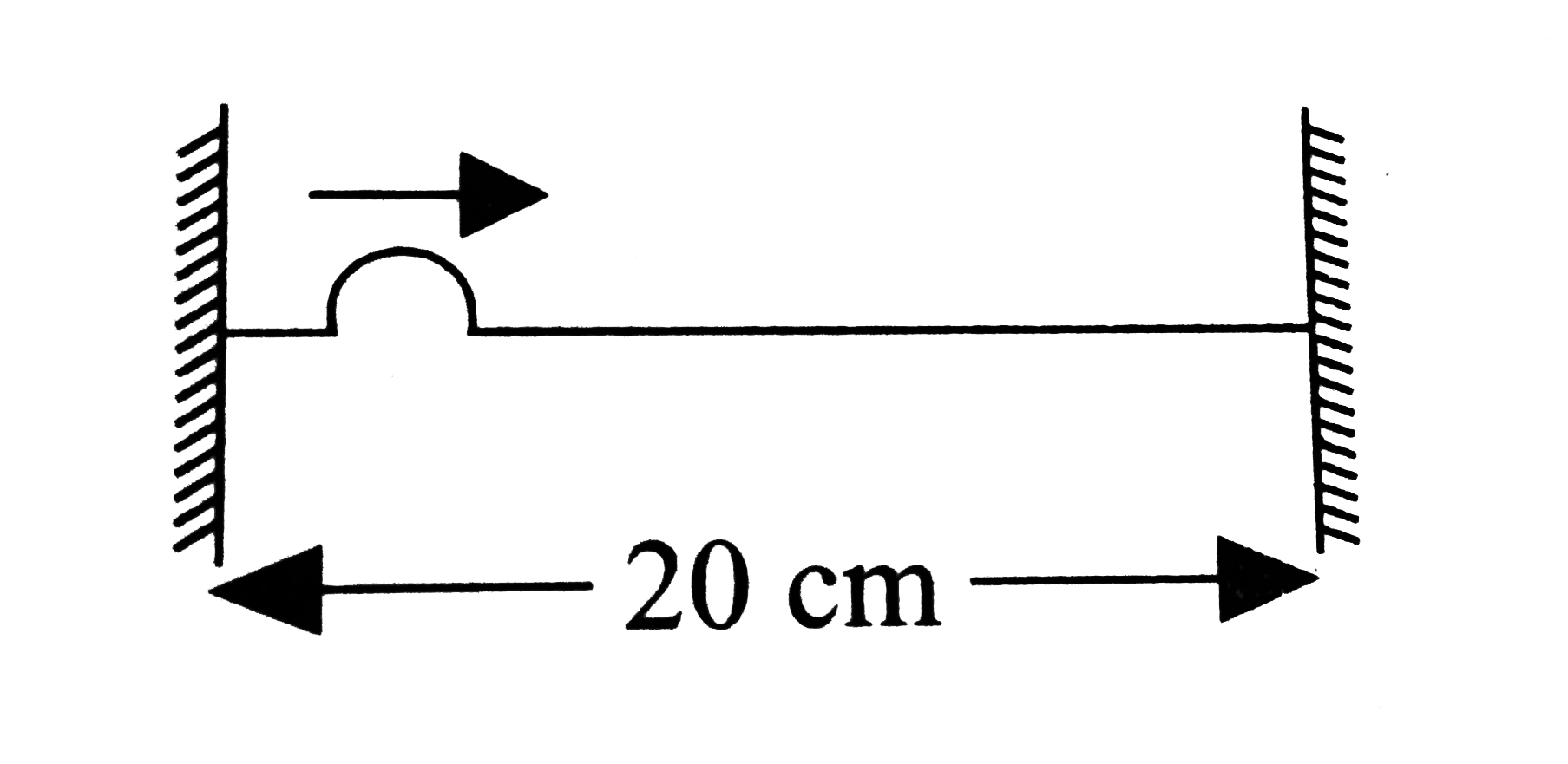
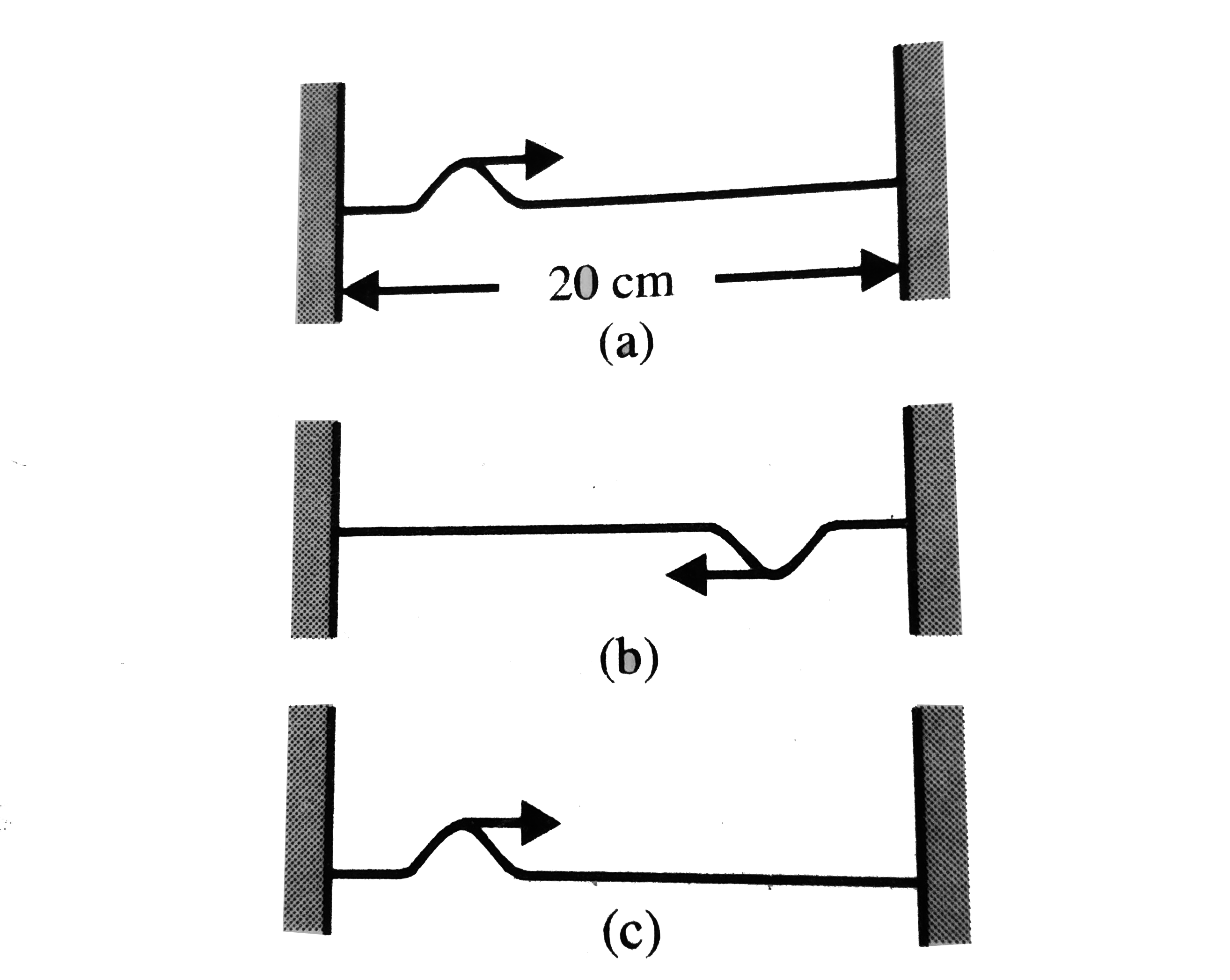
View SolutionA string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N.A wave pulse is produced at t=0 nearj an end as shown in figure which travels towards the other end.
when will the string have the shape shown in the figure again? (∈×10−2s)
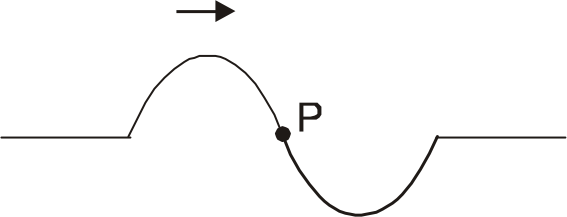
View SolutionA pulse on a string is shown in the figure.P is particle of the string.Then state which of the following are correct .
View SolutionA string of length 20cm and linear mass density 0.40g/cm is fixed at both ends and is kept under a tension of 16N . A wave pulse is produced at t=0 near an ends as shown in Fig. 7.17 (b) , which travels towards the other end . When will the string have the shape shown in the Fig . ( c).
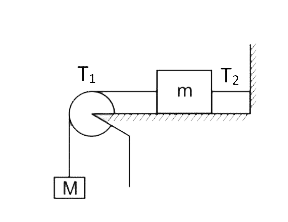
View SolutionThe tension T in the string shown in figure is

View SolutionFor the system shown in figure, the tensions in the string
View SolutionIn the given figure tension at the mid-point of string −2. If mass of string−1 is 6kg and mass of string−2 is 4kg.

View SolutionTwo particle of masses 10 kg and 35 kg are connected with four strings at points B and D as shown in fig.

Determine the tension in various segments of the string.
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA tuning fork of frequency 512 Hz is vibrated with sonometer wire and 6 beats per seconds are heard. The beat frequency reduces if the tension in the string is slightly increased. The original frequency of vibration of the string is
View Solution
