If a ball is thrown upwards from the surface of earth :
The earth remains stationary while the ball moves upwards
The ball remains stationary while the earth moves downwards
The ball and earth both move towards each other
The ball and earth both move away from each other
The correct Answer is:D
To solve the problem of a ball thrown upwards from the surface of the Earth, we can analyze the situation using the principles of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the System
When a ball is thrown upwards from the surface of the Earth, we have two objects in the system: the ball and the Earth. The ball has a mass m1 and is thrown with an initial velocity v1. The mass of the Earth is M.
Hint: Identify the two objects involved and their properties (mass and initial velocity).
Step 2: Apply Conservation of Momentum
Since there are no external forces acting on the system (the ball and the Earth), the total linear momentum of the system before and after the ball is thrown must be conserved.
Before the ball is thrown, the total momentum is:
Pinitial=0
(since both the ball and the Earth are stationary).
After the ball is thrown, the total momentum is:
Pfinal=m1v1+Mv
where v is the velocity of the Earth after the ball is thrown.
Hint: Remember that the total momentum before and after must be equal.
Step 3: Set Up the Equation
Using the conservation of momentum, we can set up the equation:
0=m1v1+Mv
Rearranging this gives:
Mv=−m1v1
Hint: Rearranging the equation helps isolate the velocity of the Earth.
Step 4: Solve for the Velocity of the Earth
From the equation Mv=−m1v1, we can solve for the velocity of the Earth:
v=−m1v1M
Hint: The negative sign indicates that the direction of the Earth's velocity is opposite to that of the ball.
Step 5: Analyze the Directions
Since the ball is moving upwards (in the positive direction), the negative sign for v indicates that the Earth is moving downwards (in the negative direction). Thus, the ball and the Earth are moving away from each other.
Hint: Consider the direction of motion for both the ball and the Earth to conclude their relative movement.
Conclusion
The correct interpretation of the scenario is that the ball and the Earth both move away from each other after the ball is thrown upwards.
Final Answer: The correct option is that the ball and the Earth both move away from each other.
When a ball is thrown upwards from the surface of the Earth, we have two objects in the system: the ball and the Earth. The ball has a mass m1 and is thrown with an initial velocity v1. The mass of the Earth is M.
Since there are no external forces acting on the system (the ball and the Earth), the total linear momentum of the system before and after the ball is thrown must be conserved.
Pinitial=0
(since both the ball and the Earth are stationary).
Pfinal=m1v1+Mv
where v is the velocity of the Earth after the ball is thrown.
Using the conservation of momentum, we can set up the equation:
0=m1v1+Mv
Rearranging this gives:
Mv=−m1v1
From the equation Mv=−m1v1, we can solve for the velocity of the Earth:
v=−m1v1M
Since the ball is moving upwards (in the positive direction), the negative sign for v indicates that the Earth is moving downwards (in the negative direction). Thus, the ball and the Earth are moving away from each other.
The correct interpretation of the scenario is that the ball and the Earth both move away from each other after the ball is thrown upwards.
Topper's Solved these Questions
Similar Questions
A particle of mass m is thrown upwards from the surface of the earth, with a velocity u. The mass and the radius of the earth are, respectively, M and R. G is gravitational constant g is acceleration due to gravity on the surface of earth. The minimum value of u so that the particle does not return back to earth is
View SolutionA particle is throws vertically upwards from the surface of earth and it reaches to a maximum height equal to the radius of earth. The radio of the velocity of projection to the escape velocity on the surface of earth is
View SolutionA tunnel is dug across the diameter of earth. A ball is released from the surface of Earth into the tunnel. The velocity of ball when it is at a distance R2 from centre of earth is (where R = radius of Earth and M = mass of Earth)
View SolutionA particle is fired vertically upwards from the surface of earth and reaches a height 6400 km. Find the initial velocity of the particle if R = 6400 km and g at the surface of earth is 10m/s2.
View SolutionA smooth tunnel is dug along the radius of earth that ends at centre. A ball is relrased from the surface of earth along tunnel. Caefficient of restitution for collision between soil at centre and ball is 0.5. Caculate the distance travelled by ball just second collision at center. Given mass of the earth is M and radius of the earth is R.
View SolutionAn objects is projected vertically upwards from the surface of the earth with a velocity 3 times the escape velocity ve from earth's surface. What will be its final velocity after escape from the earth's gravitational pull ?
View SolutionA ball is thrown upwards from the top of an incline with angle of projection θ with the vertical as shown. Take θ=60∘ and g=10m/s2 . The ball lands exactly at the foot of the incline.
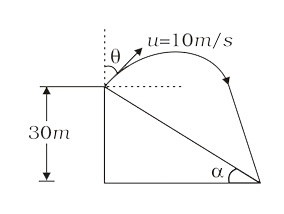
The time of flight of the ball is:
View SolutionA body is thrown from the surface of the earth with velocity u m/s. The maximum height in metre above the surface of the earth upto which it will reach is (where, R = radish of earth, g=acceleration due to gravity)
View SolutionA ball is thrown upwards from the ground with an initial speed of u. The ball is at height of 80m at two times, the time interval being 6 s. Find u. Take g=10m/s2.
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View Solution
