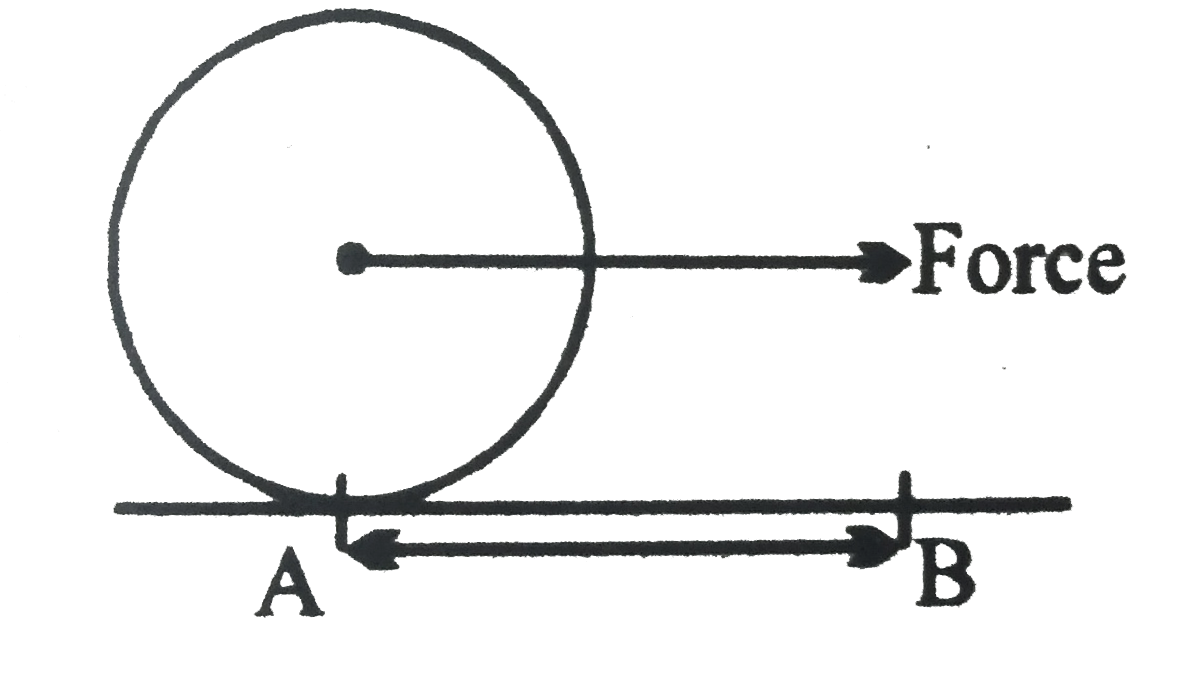
A disc of circumference s is at rest at a point A on horizontal surface when a constant horizontal force begins, to act on its centre. Between A and B there is sufficient friction to prevent slipping and the surface is smooth It the right of B,AB=s. The disc moves from A to B in time T. To the right of B.
the angular acceleration of the disc will disappear, linear acceleration will remain unchanged
linear acceleration of the disc will increase
the disc will make one rotation in time T/2
the disc will cover a distance greater then s in further time T.
The correct Answer is:A
To the right of B the friction force will disppear so α=0, linear acc. Increases so disc cover distance greater than s in time T to the right of B the ω is maximum and in T/2 one revolution will complete
Topper's Solved these Questions
Similar Questions
A disc of circumference s is at rest at a point A on a horizontal surface when a constant horizontal force begins to act on its centre. Between A and B there is sufficient friction toprevent slipping, and the surface is smooth to the right of B.AB=s. The disc moves from A to B in time T. To the right of B,
 .
.
View SolutionA body of mass 5 kg is at rest on a smooth horizontal surface. A horizontal force 'F' acts on it for 4s and then ceases to act. If the body travels 40 m in the next 5s, the value of F is,
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionThree identical cubes each of mass m are place on a smooth horizontal surface.A constant force F is applied on A as shown in the figure.The force on B applied by C is
View SolutionA force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionA sphere S rolls without slipping with a constant speed on a plank P. The friction between the upper surface of P and the sphere is sufficient to prevent slipping, while the lower surface of P is smooth and rest on the ground. Initially P is fixed on the ground by a pin N. If N is suddenly removed

View SolutionA block 'B' rests on 'A'. A rests on a horizontal surface 'C which is frictionless. There is friction between A and B. If 'B' is pulled to the right, (If P is less than frictional force between A and B)
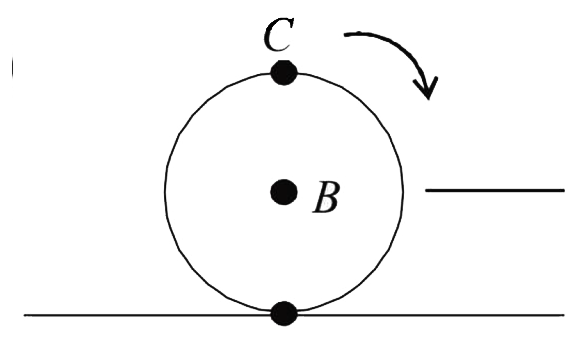
View SolutionA sphere is rolling without slipping on a fixed horizontal plane surface. In the figure, A is the point of contact, B is the centre of the sphere and C is its topmost point. Then
View Solution
