A diatomic molecules has
1 degree of freedom
3 degrees of freedom
5 degree of freedom
6 degrees of freedom
The correct Answer is:C
To determine the degrees of freedom of a diatomic molecule, we can follow these steps:
Step 1: Understand Degrees of Freedom
Degrees of freedom refer to the number of independent ways in which a molecule can move or store energy. For gas molecules, these can be translational, rotational, and vibrational.
Step 2: Identify Translational Degrees of Freedom
For any gas molecule, the translational degrees of freedom correspond to the movement in three-dimensional space. Therefore, a diatomic molecule has:
- Translational degrees of freedom = 3
Step 3: Identify Rotational Degrees of Freedom
Diatomic molecules can rotate about two axes perpendicular to the line connecting the two atoms. Thus, they have:
- Rotational degrees of freedom = 2
Step 4: Calculate Total Degrees of Freedom
To find the total degrees of freedom for a diatomic molecule, we sum the translational and rotational degrees of freedom:
- Total degrees of freedom = Translational + Rotational
- Total degrees of freedom = 3 + 2 = 5
Step 5: Conclusion
The total degrees of freedom for a diatomic molecule is 5. Therefore, the correct answer is option C.
---
Degrees of freedom refer to the number of independent ways in which a molecule can move or store energy. For gas molecules, these can be translational, rotational, and vibrational.
For any gas molecule, the translational degrees of freedom correspond to the movement in three-dimensional space. Therefore, a diatomic molecule has:
- Translational degrees of freedom = 3
Diatomic molecules can rotate about two axes perpendicular to the line connecting the two atoms. Thus, they have:
- Rotational degrees of freedom = 2
To find the total degrees of freedom for a diatomic molecule, we sum the translational and rotational degrees of freedom:
- Total degrees of freedom = Translational + Rotational
- Total degrees of freedom = 3 + 2 = 5
The total degrees of freedom for a diatomic molecule is 5. Therefore, the correct answer is option C.
Topper's Solved these Questions
Similar Questions
A diatomic molecule has dipole moment of 1.2D. If the bond distance is 1Å what parcentage of covalent in the molecule is
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
A diatomic molecule has moment of inertia I. By Bohr's quantization condition its rotational energy in the nth level (n=0 is not allowed ) is
View SolutionThe key feature of Bohr's spectrum of hydrogen atom is the quantization of angular momentum when an electron is revolving around a proton. We will extend this to a general rotational motion to find quantized rotational energy of a diatomic molecule assuming it to be rigid.The rule to be applied is Bohr's quantization condition.
A diatomic molecule has moment of inertia I. By Bohr's quantization condition its rotational energy in the nth level (n=0 is not allowed ) is
View SolutionPolar covalent molecules exhibit dipole moment. Dipole moment is equal to the product of charge separation , q and the bond length d for the bond. Unit of dipole moment is debye. One debye is equal to 10−18 esu cm.
Dipole moments is a vector quantity. It has both magnitude and direction. Hence, dipole moment of a molecule depends upon the relative orientation of the bond dipoles, but not on the polarity of bonds alone. A symmetrical structure shows zero dipole moment. Thus, dipole moment helps to predict the geometry of a molecules. Dipole moment values can be distinguish between cis- and trans- isomers, ortho, meta and pare-forms of a substance, etc.
Q. A diatomic molecule has a dipole moment of 1.2D. If the bond length is 1.0×10−8 cm, what fraction of charge does exist each atom?
View SolutionThe potential energy U of diatomic molecules as a function of separation r is shown in figure. Identify the correct stateement.
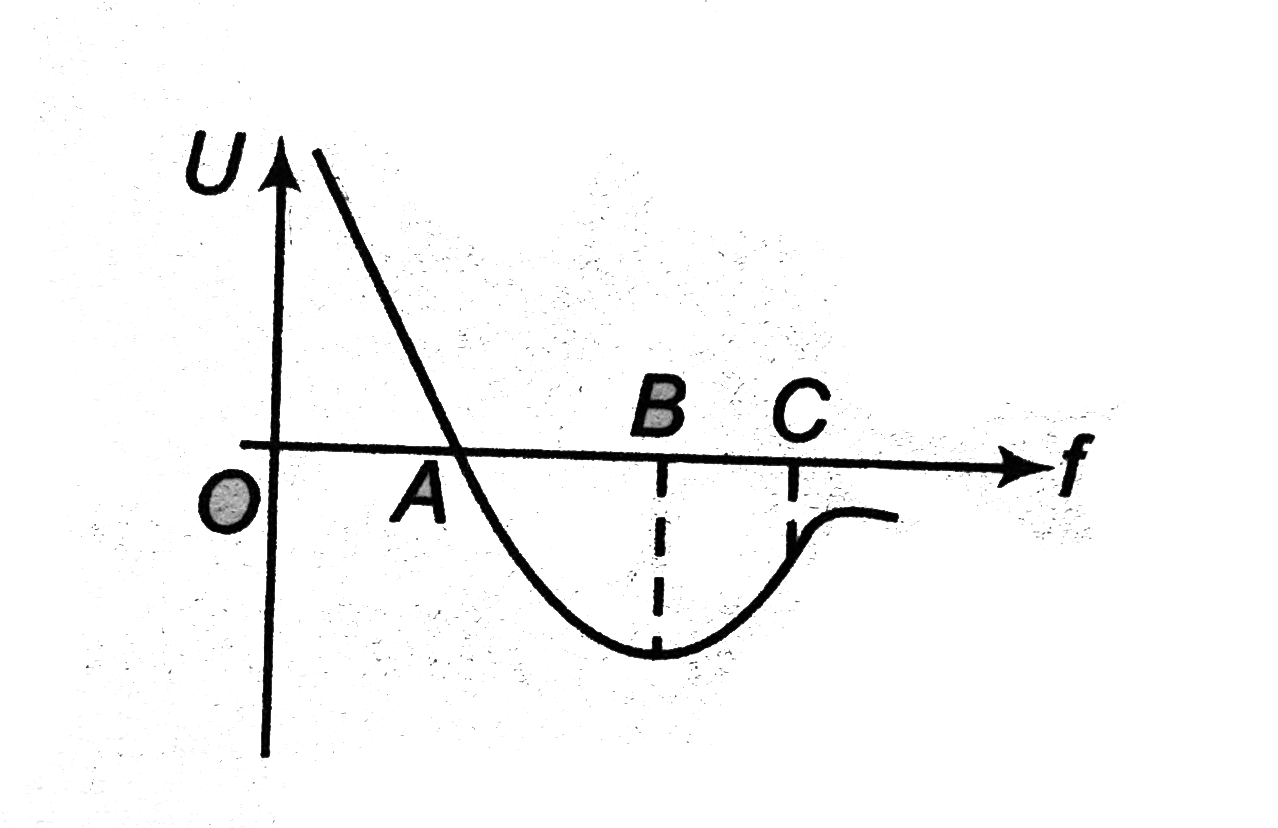
View SolutionA gas consisting of rigid di-atomic molecules (degree of freedom =5) at pressure p0=105N/m2 and temperature 273K was compressed adiabatically 5 times. The mean kinetic energy of rotating molecules in final state is nx10−21J. Find value of 'n'.(K=1.38×10−23,(5)2/5=1.90).
View SolutionThe compound having the highest bond energy among diatomic molecules is ……………… .
View SolutionThese diagrams represent the potential energy U of a diatomic molecule as a function of the inter-atomic distance r. The diagram corresponds to stable molecule found in nature is.
View SolutionAssertion : Bond energy and bond dissociation energy have identical value for diatomic molecules.
Reason : Greater the bond dissociation energy, less reactive is the bond.
View SolutionThe number of degrees of freedom of a rigid diatomic molecule is :
View Solution