A charged particle is shot with speed V towards another ifxed charged particle Q .It approaches Q up to a closest distnce r and then returns.If q were given a speed 2V, the closest distance of approach would be

r
2r
r/2
r/4
The correct Answer is:D
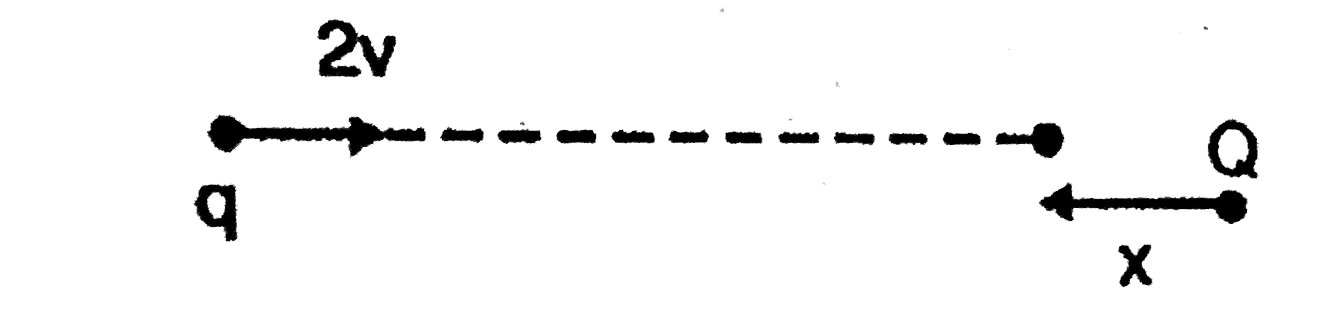
From the given data, using energy conservation
12mv2=KQqr
when particle is shot with a speed eV, let distance of closest approach =x
12m.4v2=KQqx⇒x=r4
Topper's Solved these Questions
Similar Questions
A charged particle q is shot from a large distance towards another charged particle Q which is fixed, with speed v. It approaches Q up to as closed distance r and then returns. If q were given a speed 2v, the distasnce of approach would be
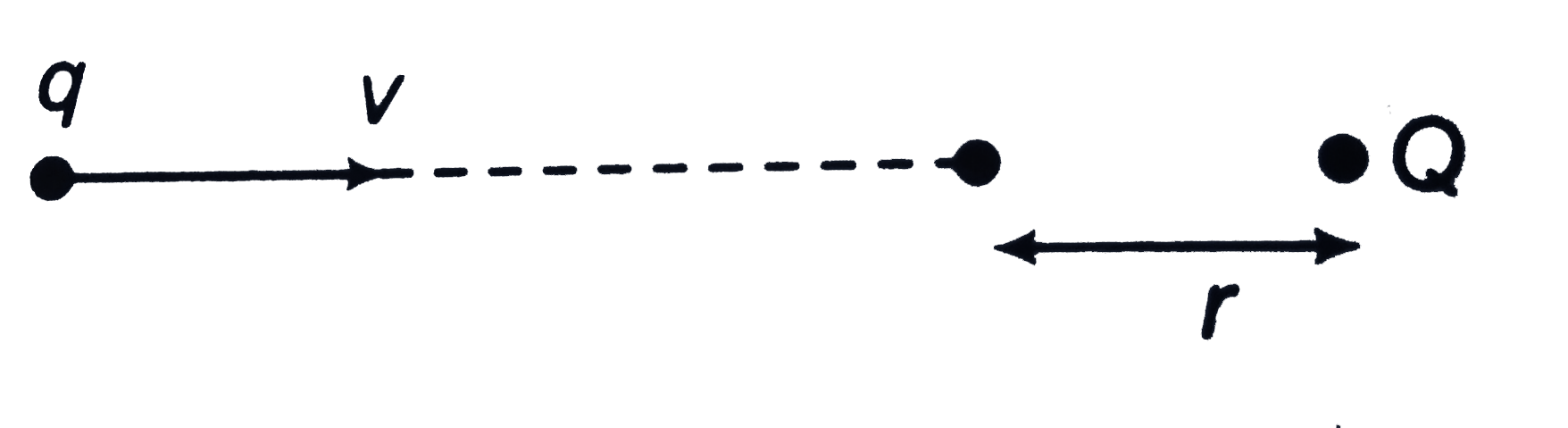
View SolutionA charged particle q is shot from a large distance towards another charged particle Q which is fixed, with speed v. It approaches Q up to as closed distance r and then returns. If q were given a speed 2v, the distasnce of approach would be

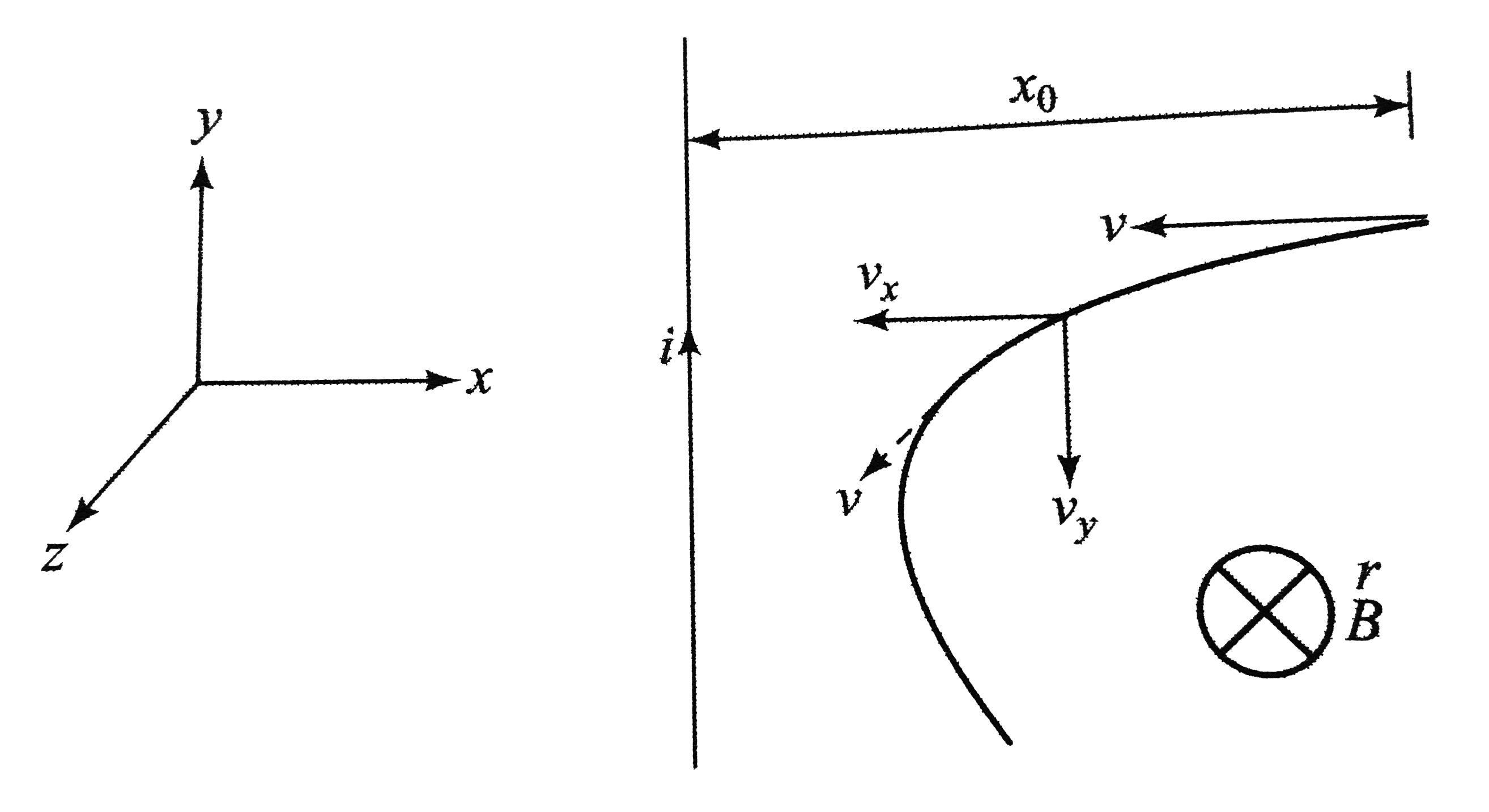
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View SolutionRutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:

(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :
View SolutionTwo identical particles of mass m carry a charge Q, each. Initially one is at rest on a smooth horizontal plane and the other is projected along the plane directly towards first particle from a large distance with speed v. The closest distance of approach be .
View SolutionA charged particle of charge 'Q' is held fixed and another charged particle of mass 'm' and charge 'q' (of the same sign) is released from a distance 'r'. The impulse of the force exerted by the external agent on the fixed charge by the time distance between 'Q' and 'q' becomes 2r is
View SolutionA charge particle q1, is at position (2, -1, 3). The electrostatic force on another charged particle q2 at (0, 0, 0) is :
View SolutionAn α- particle moving with initial kinetic energy K towards a nucleus of atomic number z approaches a distance 'd' at which it reverse its direction. Obtain the expression for the distance of closest approach 'd' in terms of the kinetic energy of α- particle K.
View SolutionA particle of mass m and charge +q approaches from a very large distance towards a uniformly charged ring ofradius Rand charge, mass same as that of particle, with initial velocity v0 along the axis of the ring as shown in the figure-1.420. What is the closest distance of approach between the ring and the particle? Assume the space to be gravity free and frictionless :

View Solution
A charge particle q of mass is placed at a distance d from another charge particle -2q of mass 2 m in a uniform magnetic field B as shown if particle are projected towareds each other with equal speed v0, so that the two particle touches each other without collision during its motion (Assume only force due to magnetic field acts on the particle)
View Solution
