The distance of nth bright fringe to the (n+1)th dark fringe in Young's experiment is equal to:
nλDd
nλD2d
λD2d
λDd
The correct Answer is:C
To solve the problem, we need to find the distance between the nth bright fringe and the (n+1)th dark fringe in Young's double-slit experiment.
1. Understanding Bright and Dark Fringes:
- The position of the nth bright fringe is given by the formula:
yb=nλDd
where yb is the position of the nth bright fringe, λ is the wavelength of light, D is the distance from the slits to the screen, and d is the distance between the slits.
2. Position of Dark Fringes:
- The position of the nth dark fringe is given by:
yd=(2n−1)λD2d
- For the (n+1)th dark fringe, the position is:
yd(n+1)=(2(n+1)−1)λD2d=(2n+1)λD2d
3. Distance Between Bright and Dark Fringe:
- Now, we need to find the distance between the nth bright fringe and the (n+1)th dark fringe:
Δy=yd(n+1)−yb
- Substituting the expressions for yd(n+1) and yb:
Δy=(2n+1)λD2d−nλDd
4. Simplifying the Expression:
- To simplify, we can find a common denominator:
Δy=(2n+1)λD2d−2nλD2d
- This simplifies to:
Δy=(2n+1−2n)λD2d=λD2d
5. Final Result:
- Therefore, the distance between the nth bright fringe and the (n+1)th dark fringe is:
Δy=λD2d
Final Answer:
The distance of the nth bright fringe to the (n+1)th dark fringe in Young's experiment is equal to λD2d.
- The position of the nth bright fringe is given by the formula:
yb=nλDd
where yb is the position of the nth bright fringe, λ is the wavelength of light, D is the distance from the slits to the screen, and d is the distance between the slits.
- The position of the nth dark fringe is given by:
yd=(2n−1)λD2d
- For the (n+1)th dark fringe, the position is:
yd(n+1)=(2(n+1)−1)λD2d=(2n+1)λD2d
- Now, we need to find the distance between the nth bright fringe and the (n+1)th dark fringe:
Δy=yd(n+1)−yb
- Substituting the expressions for yd(n+1) and yb:
Δy=(2n+1)λD2d−nλDd
- To simplify, we can find a common denominator:
Δy=(2n+1)λD2d−2nλD2d
- This simplifies to:
Δy=(2n+1−2n)λD2d=λD2d
- Therefore, the distance between the nth bright fringe and the (n+1)th dark fringe is:
Δy=λD2d
The distance of the nth bright fringe to the (n+1)th dark fringe in Young's experiment is equal to λD2d.
Topper's Solved these Questions
Similar Questions
The distance of nth bright fringe to the nth dark fringe in Young's experiment is equal to
View SolutionIn Young's double slit experiment separation between slits is 1mm, distance of screen from slits is 2m. If wavelength of incident light is 500 nm. Determine
(i) fringe width
(ii) angular fringe width
(iii) distance between 4 th bright fringe and 3rd dark fringe
(iv) If whole arrangement is immersed in water (μw=4/3), new angular fringe width.
View Solution
Knowledge Check
A beam of light consisting of two wavelengths 650nm and 520nm is used to obtain interference fringes in a Young's double slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 650nm.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide? The distance between the slits is 2mm and the distance between the plane of the slits and screen is 120cm.A1.17 mmB2.52 mmC1.56 mmD3.14 mm
A beam of light consists of two wavelengths, 6300Åand5600Å. This beam of light is used to obtain an interference pattern in YDSE. If 4th bright fringe of 6300Å coincides with the nth dark fringe of 5600Å from the central line, then find the value of n.
View SolutionIn a Young's double-slit experiment , the slits are separated by 0.28 mm and screen is placed 1.4 m away . The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm . Determine the wavelength of light used in the experiment .
View SolutionIn a Young's double-slit experiment , the slits are separated by 0.28 mm and screen is placed 1.4 m away . The distance between the central bright fringe and the fourth bright fringe is measured to be 1.2 cm . Determine the wavelength of light used in the experiment .
View SolutionHow does the fringe width of interference fringes change, when the whole apparatus of Young's experiment is kept in a liquid of refractive index 1.3 ?
View SolutionA beam of light consisting of two wavelength 6300A∘ and λA∘ is used to obtain interference frings in a Young's double slit experiment. If 4th bright fringe of 6300A∘ coincides with 5th dark fringe of λA∘, the value of λ(inA∘) is
View SolutionIn the figure is shown Young's double slit experiment. Q is the position of the first bright fringe on the right side of O. P is the 11th bright fringe on the other side, as measured from Q. If the wavelength of the light used is 600nm. Then S1B will be equal to
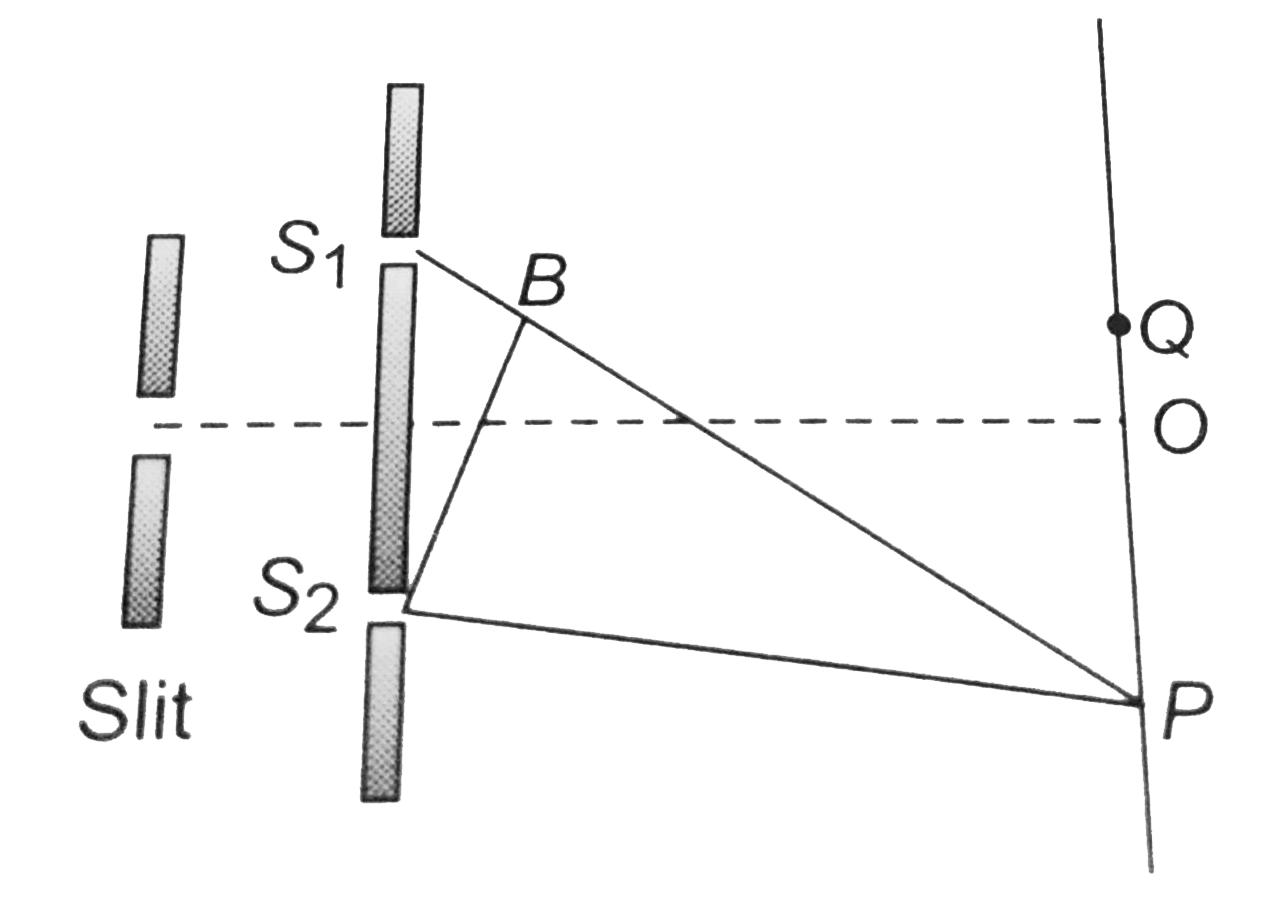
View SolutionAnswer the following:
(a) what are coherent sources of light ? Two slits in Young's double slit experiments are illuminated by two different sodium lamps emitting light of the same wavelength. Why is no interference pattern observed?
(b) Obtain the condition for getting dark and bright fringes in Young's experiment. Hence write the expression for the fringe width.
(c) If s is the size of the source and its distance from the plane of the two slits, what should be the criterion for the interference fringes to be seen?
View Solution
