According to Moseley's law, the ratio of the slope of graph between √f and Z for Kβ and Kα is
√3227
√2732
√3322
√2233
The correct Answer is:A
To solve the problem regarding Moseley's law and the ratio of the slope of the graph between √f and Z for Kβ and Kα, we can follow these steps:
1. Understanding Moseley's Law: According to Moseley's law, the frequency f of the X-ray emitted by an atom can be expressed as:
f∝(Z−1)2
where Z is the atomic number.
2. Frequency Expressions for Kα and Kβ:
- For Kα transition (where n=2):
fα=R⋅(Z−1)2⋅(112−122)=R⋅(Z−1)2⋅(1−14)=R⋅(Z−1)2⋅34
Thus, we can write:
√fα=√R⋅(Z−1)⋅√34
- For Kβ transition (where n=3):
fβ=R⋅(Z−1)2⋅(112−132)=R⋅(Z−1)2⋅(1−19)=R⋅(Z−1)2⋅89
Thus, we can write:
√fβ=√R⋅(Z−1)⋅√89
3. Finding the Slopes:
- The slope of the graph of √f vs Z for Kα is:
mα=√R⋅√34
- The slope of the graph of √f vs Z for Kβ is:
mβ=√R⋅√89
4. Calculating the Ratio of Slopes:
- The ratio of the slopes mβmα is:
mβmα=√R⋅√89√R⋅√34
- Simplifying this gives:
=√89√34=√8⋅√4√9⋅√3=4√23√3=4√23√3
5. Final Ratio:
- The final ratio of the slopes is:
mβmα=89÷34=8⋅49⋅3=3227
Conclusion:
The ratio of the slope of the graph between √f and Z for Kβ and Kα is 3227.
f∝(Z−1)2
where Z is the atomic number.
- For Kα transition (where n=2):
fα=R⋅(Z−1)2⋅(112−122)=R⋅(Z−1)2⋅(1−14)=R⋅(Z−1)2⋅34
Thus, we can write:
√fα=√R⋅(Z−1)⋅√34
fβ=R⋅(Z−1)2⋅(112−132)=R⋅(Z−1)2⋅(1−19)=R⋅(Z−1)2⋅89
Thus, we can write:
√fβ=√R⋅(Z−1)⋅√89
- The slope of the graph of √f vs Z for Kα is:
mα=√R⋅√34
- The slope of the graph of √f vs Z for Kβ is:
mβ=√R⋅√89
- The ratio of the slopes mβmα is:
mβmα=√R⋅√89√R⋅√34
- Simplifying this gives:
=√89√34=√8⋅√4√9⋅√3=4√23√3=4√23√3
- The final ratio of the slopes is:
mβmα=89÷34=8⋅49⋅3=3227
The ratio of the slope of the graph between √f and Z for Kβ and Kα is 3227.
Topper's Solved these Questions
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Exercise-2 part-II Single and double value integer type
Explore 12 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Exercise-2 part-III one or more than one options correct type
Explore 14 Videos
- ATOMIC PHYSICSBook:RESONANCE ENGLISHChapter:ATOMIC PHYSICSExercise:Exercise ( Part II : Only one one correct type)
Explore 37 Videos
- ALTERNATING CURRENTBook:RESONANCE ENGLISHChapter:ALTERNATING CURRENTExercise:HIGH LEVEL PROBLEMS
Explore 11 Videos
- CAPACITANCEBook:RESONANCE ENGLISHChapter:CAPACITANCEExercise:High Level Problems
Explore 16 Videos
Similar Questions
According to Moseley.s law, the frequency of a spectral line in X-ray spectrum varies as
View SolutionAccording to moselay.s law, the frequency (ϑ) of the Kα line and the atomic number (z) of the element have the relation (A and B) are constants
View SolutionIn Moseley's law √v=a(z−b), the volue of the screening constant for K-series and L-series of X-rays are respectively
View Solution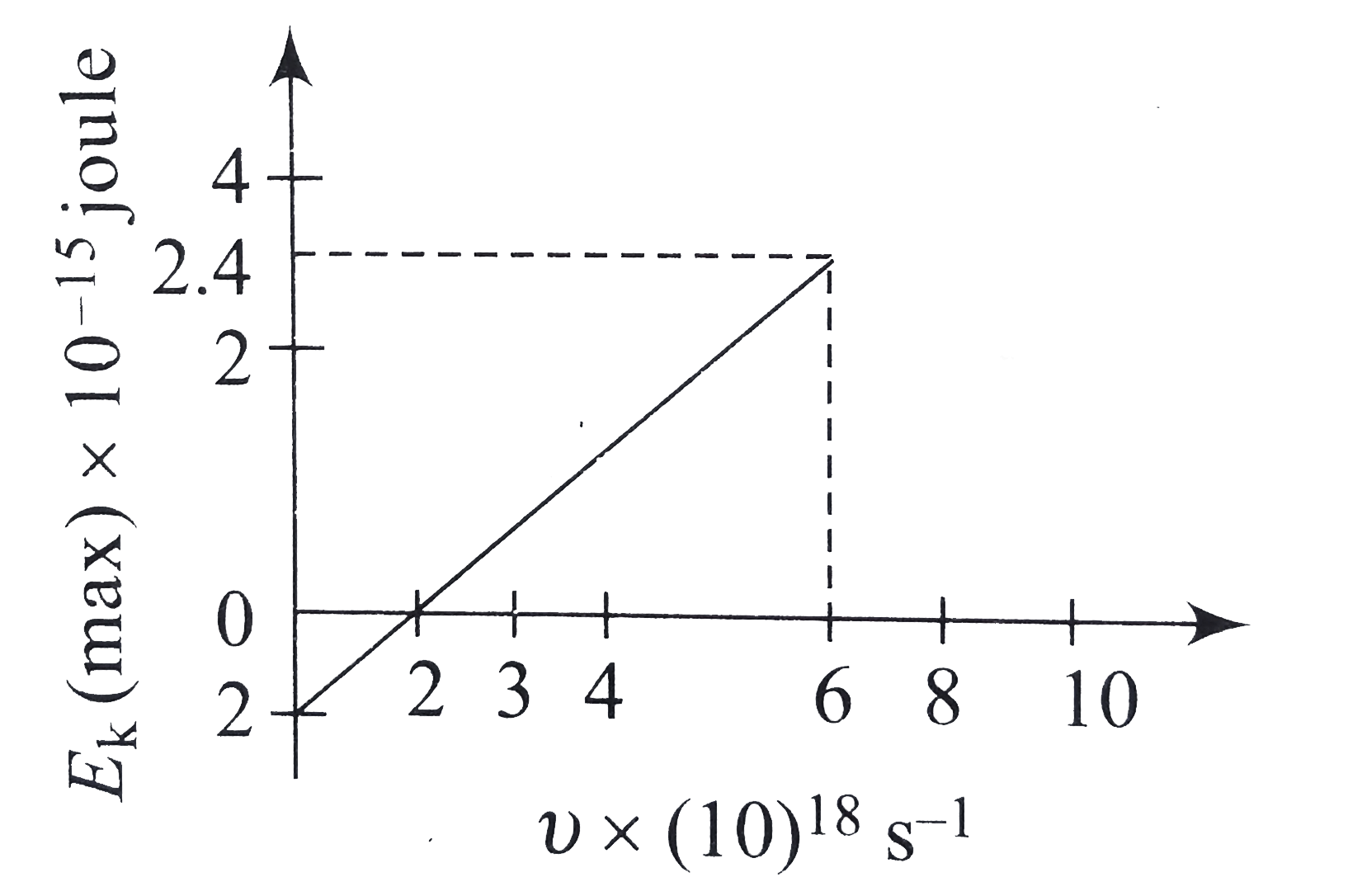
In the experiment on photoelectric effect, the graph between EK(max) and v is found to be a straight line as sshoen in fig. The threshold frequency and Planck's constant according to this graph are
View SolutionIn the Moseley relation, √v=a(Z−b) which will have the greater value for the constant a for Kα or Kβ transition?
View SolutionMoseley's law for characteristic X-rays is √v=a(Z−b). In this,
View SolutionUse Moseley's law with b=1 to find the frequency of the Kα X-rays of La (Z=57) , if the frequency of the Kα X-rays of Cu (Z=29) is know to be 1.88×1018Hz.
View SolutionUse Moseley's law with b = 1 to find the frequency of the Kα X-ray of La(Z=57) if the frequency of the Kα X-ray of Cu(Z=29) is known to be 1⋅88×1018 Hz.
View SolutionUse Moseley's law with b = 1 to find the frequency of the Kα X-ray of La(Z=57) if the frequency of the Kα X-ray of Cu(Z=29) is known to be 1⋅88×1018 Hz.
View SolutionFigure shown Moseley's plot between √f and Z where f is the frequency and Z is the atomic number. Three lines A, B, and C always in the graph may repersent

View Solution