A dence collection of equal number of electrona and positive ions is called netural plasma. Certain solids contianing fixed positive ions surroundedby free electrons can be treated as neytral plasma. Let 'N' be the numbrer density of free electrons, each of mass 'm'. When the elctrons are subjected to an eletric field, they are displaced relatively away from the heavy positive ions. if the electric field becomes zero, the electrons begin to oscillate about the positive ions with a natural angular frequency 'ωP' which is called the plasma frequency. to sustain the oscillations, a time varying electric field needs to be applied that has an angular frequrncy ω, where a part of the energy is absorbed and a part of it is reflected. As ω approaches ωp all the free electrons are set to resonance together and all the energy is reflected. this is the explaination of high reflectivity of metals.
(2) Estimate the wavelength at which plasma reflection will occur for a metal having the density of electrons N≈4×1027m−3. Taking ε0=1011 and mass m≈10−30, where these quantities are in proper SI units.
800nm
600nm
300nm
200nm
The correct Answer is:B
To estimate the wavelength at which plasma reflection will occur for a metal with an electron density N=4×1027m−3, we will follow these steps:
Step 1: Understand the Plasma Frequency Formula
The plasma frequency ωp is given by the formula:
ωp=√Ne2mϵ0
where:
- N is the number density of free electrons,
- e is the charge of an electron (e≈1.6×10−19C),
- m is the mass of an electron (m≈10−30kg),
- ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12F/m).
Step 2: Relate Angular Frequency to Wavelength
The angular frequency ω can be related to the frequency f and wavelength λ as follows:
ω=2πf=2πcλ
where c is the speed of light (c≈3×108m/s).
Step 3: Set Up the Equation
At resonance, we set ω=ωp:
2πcλ=√Ne2mϵ0
Step 4: Solve for Wavelength λ
Rearranging the equation to solve for λ:
λ=2πc√Ne2mϵ0
Step 5: Substitute the Known Values
Now, substitute the known values into the equation:
- N=4×1027m−3
- e=1.6×10−19C
- m=10−30kg
- ϵ0=8.85×10−12F/m
- c=3×108m/s
Calculating λ:
λ=2π(3×108)√(4×1027)(1.6×10−19)2(10−30)(8.85×10−12)
Step 6: Calculate the Denominator
Calculating the denominator:
(4×1027)(1.6×10−19)2(10−30)(8.85×10−12)=(4×1027)(2.56×10−38)(10−30)(8.85×10−12)
=10.24×10−118.85×10−12≈1.157×101≈11.57
Step 7: Calculate √11.57
√11.57≈3.4
Step 8: Final Calculation of Wavelength
Now substituting back:
λ=2π(3×108)3.4≈6.2832×3×1083.4≈1.88496×1093.4≈554.4nm
Conclusion
The estimated wavelength at which plasma reflection will occur is approximately 554.4nm.
The plasma frequency ωp is given by the formula:
ωp=√Ne2mϵ0
where:
- N is the number density of free electrons,
- e is the charge of an electron (e≈1.6×10−19C),
- m is the mass of an electron (m≈10−30kg),
- ϵ0 is the permittivity of free space (ϵ0≈8.85×10−12F/m).
The angular frequency ω can be related to the frequency f and wavelength λ as follows:
ω=2πf=2πcλ
where c is the speed of light (c≈3×108m/s).
At resonance, we set ω=ωp:
2πcλ=√Ne2mϵ0
Rearranging the equation to solve for λ:
λ=2πc√Ne2mϵ0
Now, substitute the known values into the equation:
- N=4×1027m−3
- e=1.6×10−19C
- m=10−30kg
- ϵ0=8.85×10−12F/m
- c=3×108m/s
λ=2π(3×108)√(4×1027)(1.6×10−19)2(10−30)(8.85×10−12)
Calculating the denominator:
(4×1027)(1.6×10−19)2(10−30)(8.85×10−12)=(4×1027)(2.56×10−38)(10−30)(8.85×10−12)
=10.24×10−118.85×10−12≈1.157×101≈11.57
√11.57≈3.4
Now substituting back:
λ=2π(3×108)3.4≈6.2832×3×1083.4≈1.88496×1093.4≈554.4nm
The estimated wavelength at which plasma reflection will occur is approximately 554.4nm.
Topper's Solved these Questions
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems
17 Videos
- ATOMIC PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Exercise-2 Part-III : Comprehension
12 Videos
- ALTERNATING CURRENTBOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - HIGH LEVEL PROBLEMS
11 Videos
- CAPACITANCEBOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems
16 Videos
Similar Questions
A dence collection of equal number of electrona and positive ions is called netural plasma. Certain solids contianing fixed positive ions surroundedby free electrons can be treated as neytral plasma. Let 'N' be the numbrer density of free electrons, each of mass 'm'. When the elctrons are subjected to an eletric field, they are displaced relatively away from the heavy positive ions. if the electric field becomes zero, the electrons begin to oscillate about the positive ions with a natural angular frequency 'ωP' which is called the plasma frequency. to sustain the oscillations, a time varying electric field needs to be applied that has an angular frequrncy ω, where a part of the energy is absorbed and a part of it is reflected. As ω approaches ωp all the free electrons are set to resonance together and all the energy is reflected. this is the explaination of high reflectivity of metals.
(1) Taking the electronic charge as 'e' and the permittivity as 'ε0'. use dimensional analysis to determine the correct expression for ωp.
View SolutionGive reason : Metals form positive ions.
View Solution
Knowledge Check
The loss of positive ions from the interior of a neuron produces
AdepolarisationBthresholdChyperpolarisationDaction potential
An atom that loses one or more electrons to form a positive ion is called a ____
View SolutionThe position of the point where the net electric field will be zero is
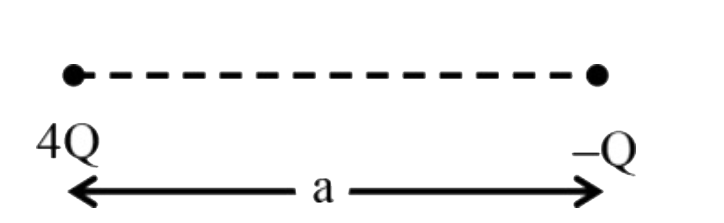
View SolutionNumber of valence electrons in Cl– ion are:
View SolutionNumber of valence electrons in Cl– ion are:
View SolutionThe total number of valence electrons in 4.2g of N−3 ion are :
View SolutionAn atom that loses electrons becomes a positively-charged ion called
View SolutionA dispositive ion 16 protons what is the number of electron is its tetrapositive ion?
View Solution
