If the wavelength of photon emitted from an electron jump to in a like species is then the species is
atom
ion
ion
ion
The correct Answer is:2
To determine the species of the hydrogen-like ion based on the given photon emission wavelength, we will follow these steps:
Step 1: Calculate the Energy of the Photon
The energy of a photon can be calculated using the formula:
E=hcλ
where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3.00×108m/s),
- λ is the wavelength in meters.
First, convert the wavelength from angstroms to meters:
λ=1216Å=1216×10−10m
Now, substituting the values into the energy formula:
E=(6.626×10−34J s)(3.00×108m/s)1216×10−10m
Calculating this gives:
E≈1.64×10−18J
To convert this energy into electron volts (1 eV = 1.602×10−19J):
E≈1.64×10−181.602×10−19≈10.24eV
Step 2: Identify the Transition
The energy calculated corresponds to the transition of an electron from a higher energy level to a lower energy level. In hydrogen-like species, the energy levels can be described by the formula:
En=−Z2⋅13.6eVn2
where Z is the atomic number of the ion.
The energy difference between levels n=4 and n=2 can be calculated as:
ΔE=E4−E2=−Z2⋅13.642+Z2⋅13.622
=Z2⋅13.6(14−116)=Z2⋅13.6(4−116)=Z2⋅13.6⋅316
Setting this equal to the energy we calculated:
Z2⋅13.6⋅316=10.24
Step 3: Solve for Z
Rearranging gives:
Z2=10.24⋅1613.6⋅3
Calculating the right-hand side:
Z2=163.8440.8≈4
Thus, Z=2.
Conclusion
Since Z=2, the species is Helium ion (He+), which is a hydrogen-like species.
Final Answer
The species is Helium ion (He+).
---
The energy of a photon can be calculated using the formula:
E=hcλ
where:
- E is the energy of the photon,
- h is Planck's constant (6.626×10−34J s),
- c is the speed of light (3.00×108m/s),
- λ is the wavelength in meters.
λ=1216Å=1216×10−10m
E=(6.626×10−34J s)(3.00×108m/s)1216×10−10m
E≈1.64×10−18J
E≈1.64×10−181.602×10−19≈10.24eV
The energy calculated corresponds to the transition of an electron from a higher energy level to a lower energy level. In hydrogen-like species, the energy levels can be described by the formula:
En=−Z2⋅13.6eVn2
where Z is the atomic number of the ion.
ΔE=E4−E2=−Z2⋅13.642+Z2⋅13.622
=Z2⋅13.6(14−116)=Z2⋅13.6(4−116)=Z2⋅13.6⋅316
Z2⋅13.6⋅316=10.24
Rearranging gives:
Z2=10.24⋅1613.6⋅3
Calculating the right-hand side:
Z2=163.8440.8≈4
Thus, Z=2.
Since Z=2, the species is Helium ion (He+), which is a hydrogen-like species.
The species is Helium ion (He+).
Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Inorganic chemistry (Chemistry Bonding)
38 Videos
- ATOMIC STRUCTUREBOOK - RESONANCE ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
16 Videos
- AROMATIC COMPOUNDS BOOK - RESONANCE ENGLISHCHAPTER - AROMATIC COMPOUNDS EXERCISE - PART-II : JEE (MAIN)
1 Videos
- CHEMICAL BONDINGBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL BONDINGEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
6 Videos
Similar Questions
Calculate wavelength of photon emitted when an electron goes from n=3 to n=2 level of hydrogen atom.
View SolutionThe wavelength of the radiation emitted when an electron falls from Bohr 's orbit 4 to 2 in H atom is
View SolutionCalculate the wavelength of a photon emitted when an electron in H− atom maker a transition from n=2 to n=1
View SolutionWhen electron jumps from n = 4 to n = 1 orbit, we get
View SolutionIf the wavelength of photon emitted due to transition of electron from third orbit to first orbit in a hydrogen atom is λ then the wavelength of photon emitted due to transition of electron from fourth orbit to second orbit will be
View SolutionIn a set of experiment on a hydrogen on a hypotherical one-electron atom, the wavelength of the photons emitted from transition ending in the ground state (n=1) are shown in the energy level diagram
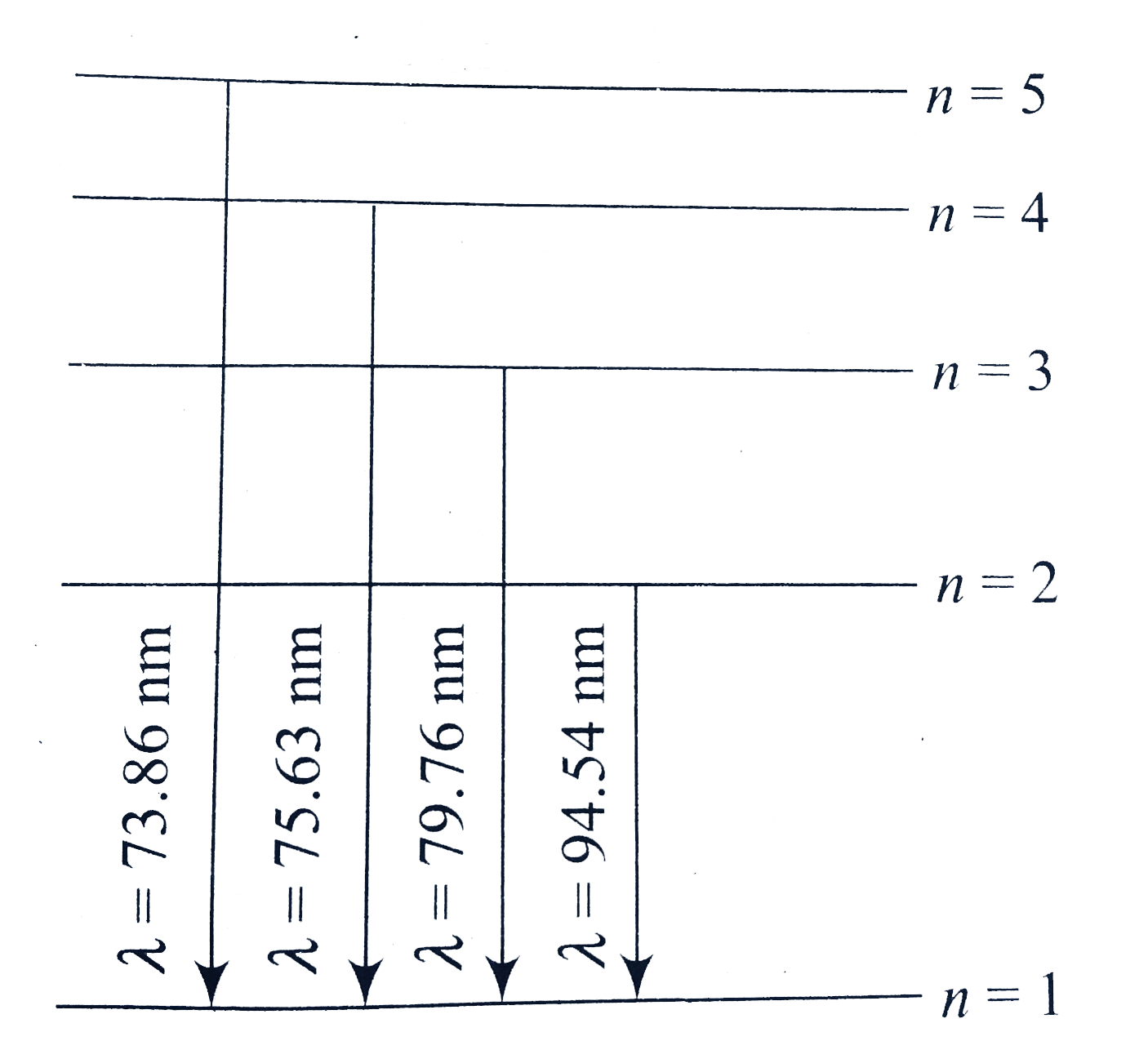
λ5→1=73.86nm
λ4→1=75.63nm
λ3→1=79.76nm
λ2→1=94.54nm
If an electron made a transition from n = 4 to n = 2 level, the wavelength of the light that it would emit is nearly
View SolutionThe ionization energy of a hydrogen like bohr atom is 4 Rydbergs (i) What is the wavelength of the radiation emitted when the electron jumps from the first excited state to the ground state ?(ii) what is the radius of the orbit for this atom ?
View SolutionCalculate the wavelength of the spectral line when an electron jumps from n=7 to n=4 level in an atom of hydrogen.
View SolutionWhat is the wavelength of the radiation emitted when the electron in a hydrogen atom jumps from n=→n=2?
View SolutionCalculate the energy and frequency of the radiation emitted when an electron jumps from n=3 to n=2 in a hydrogen atom.
View Solution
