1 mol of a gaseous aliphatic compound is completely burnt in an excess of oxygen. The contraction in volume in (assume water gets condensed out ):
The correct Answer is:4
To solve the problem of finding the contraction in volume when 1 mole of the gaseous aliphatic compound CnH3nOm is completely burnt in excess oxygen, we can follow these steps:
Step 1: Determine the products of combustion
When a hydrocarbon burns in oxygen, it produces carbon dioxide (CO₂) and water (H₂O). The general combustion reaction can be represented as follows:
CnH3nOm+O2→CO2+H2O
Step 2: Write the balanced equation for combustion
From the combustion of CnH3nOm, we can derive the moles of products formed:
- Each mole of carbon (C) produces 1 mole of CO2.
- Each 2 moles of hydrogen (H) produce 1 mole of H2O.
Thus, the combustion of CnH3nOm will produce:
- n moles of CO2
- 3n2 moles of H2O
Step 3: Calculate the moles of oxygen required
To find the moles of oxygen (O2) required for the reaction, we can use the following formula:
Moles of O2=Moles of CO2+12Moles of H2O−12Moles of O
Substituting the values:
Moles of O2=n+3n4−m2
Step 4: Total moles before and after combustion
Initially, we have:
- 1 mole of CnH3nOm (the reactant)
- Moles of O2 consumed (which we calculated)
The total moles before combustion:
Total moles before=1+Moles of O2
The total moles after combustion:
Total moles after=n+3n2
Step 5: Calculate the contraction in volume
The contraction in volume can be calculated as:
Contraction=Total moles before−Total moles after
Substituting the values:
Contraction=(1+n+3n4−m2)−(n+3n2)
Simplifying this expression gives:
Contraction=1+3n4−m2−n−3n2
=1+3n4−n−3n2−m2
=1+3n4−4n4−6n4−m2
=1−7n4−m2
Final Result
Thus, the contraction in volume when 1 mole of the compound CnH3nOm is completely burnt in excess oxygen is:
Contraction=1−7n4−m2
When a hydrocarbon burns in oxygen, it produces carbon dioxide (CO₂) and water (H₂O). The general combustion reaction can be represented as follows:
CnH3nOm+O2→CO2+H2O
From the combustion of CnH3nOm, we can derive the moles of products formed:
- Each mole of carbon (C) produces 1 mole of CO2.
- Each 2 moles of hydrogen (H) produce 1 mole of H2O.
- n moles of CO2
- 3n2 moles of H2O
To find the moles of oxygen (O2) required for the reaction, we can use the following formula:
Moles of O2=Moles of CO2+12Moles of H2O−12Moles of O
Substituting the values:
Moles of O2=n+3n4−m2
Initially, we have:
- 1 mole of CnH3nOm (the reactant)
- Moles of O2 consumed (which we calculated)
Total moles before=1+Moles of O2
Total moles after=n+3n2
The contraction in volume can be calculated as:
Contraction=Total moles before−Total moles after
Substituting the values:
Contraction=(1+n+3n4−m2)−(n+3n2)
Simplifying this expression gives:
Contraction=1+3n4−m2−n−3n2
=1+3n4−n−3n2−m2
=1+3n4−4n4−6n4−m2
=1−7n4−m2
Thus, the contraction in volume when 1 mole of the compound CnH3nOm is completely burnt in excess oxygen is:
Contraction=1−7n4−m2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - GASEOUS STATEEXERCISE - INORGANIC CHEMISTRY (COORDINATION COMPOUNDS)36videos
GASEOUS STATE
- BOOK - RESONANCE ENGLISHCHAPTER - GASEOUS STATEEXERCISE - ORGANIC CHEMISTRY(Hydrocarbon)18videos
GASEOUS STATE
- BOOK - RESONANCE ENGLISHCHAPTER - D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS EXERCISE - Match the column1videos
D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS
- BOOK - RESONANCE ENGLISHCHAPTER - GENERAL ORGANIC CHEMISTRY IIEXERCISE - Part-III: Section-5: Matching List Type1videos
GENERAL ORGANIC CHEMISTRY II
Similar Questions
1 ml of gaseous aliphatic compound CnH3nOm is completely burnt in an excess of O2 . The contraction in volume is
View SolutionWhen a gaseous olefinic hydrocarbon is burnt completely in excess of O2, a contraction in volume equal to double to the volume of hydrocarbon is noticed then hydrocarbon will be
View Solution50 ml Toluene [C6H5CH3(g)] undergoes combustion with excess of oxygen. Calculate the volume contraction.
View Solution16 " mL of " a gaseous compound CnH3nOm was mixed with 60 " mL of " O2 and sparked. The gas mixture on cooling occupied 44 mL. After treatment with NaOH solution, the volume of gas remaining was 12 mL. Deduce the formula of the compound.
View Solution(a). IF both (A) and (R) are correct and (R) is the correct explanation of (A).
(b). If both (A) and (R) are correct but (R) is not the correct explanation of (A).
(c). If (A) is correct, but (R) is incorrect.
(d). If (A) is incorrect, but (R) is correct. ltbr> (e) if both (A) and (R) are incorrect.
Q. Assertion (A): When gaseous hydrocarbon are completely burnt in eudiometer tube with excess of O2 and after cooling there is a contraction in the volume of gases.
Reason (R): The volume of H2O is not considered.View Solution11.6 g of an organic compound having formula (CnH2n+2) is burnt in excess of O2(g) initially taken in a 22.41 litre steel vessel. Reaction the gaseous mixture was at 273 K with pressure reading 2 atm. After complete complete combustion and loss of considerable amount of heat, the mixture of product and excess of O2 had a temperature of 546 K and 4.6 atm pressure. The formula of organic compound is :
View Solution11.6g of an organic compound having formula CnH2n+2 is burnt in excess of O2(g) initially taken in a 22.41 litre steel vessel. Before reactio0n the gaseous mixture was at 273K with pressure reading 2 atm. Aftercomplete combustion and loss of considerable amount of heat, the mixture of product and excess of O2 had a temperature of 546Kand4.6 atm pressure. The formula of organic compound is :
View SolutionA 20 mL mixture of CO, CH4, and Helium (He) gases is exploded by an electric discharge at room temperature with excess of oxygen. The volume contraction is found to be 13 mL. A further contraction of 14 mL occurs when the residual gas is treated wityh KOH solution. Find out the composition of the gaseous mixture in terms of volume percentage.
View SolutionAt S.T.P. a mixture of 280 mL of CH4 and 140 mL of H2 is completely burnt. Calculate the required volume of oxygen and weight of water formed, assuming that whole of the steam condenses to water.
View SolutionTwenty millilitres of a gaseous hydrocarbon (A) was exploded with excess of oxygen in eudiometer tube. On cooling, the volume was reduced by 50ml. On further treatement with KOH solution, there was a further contraction of 40 ml.
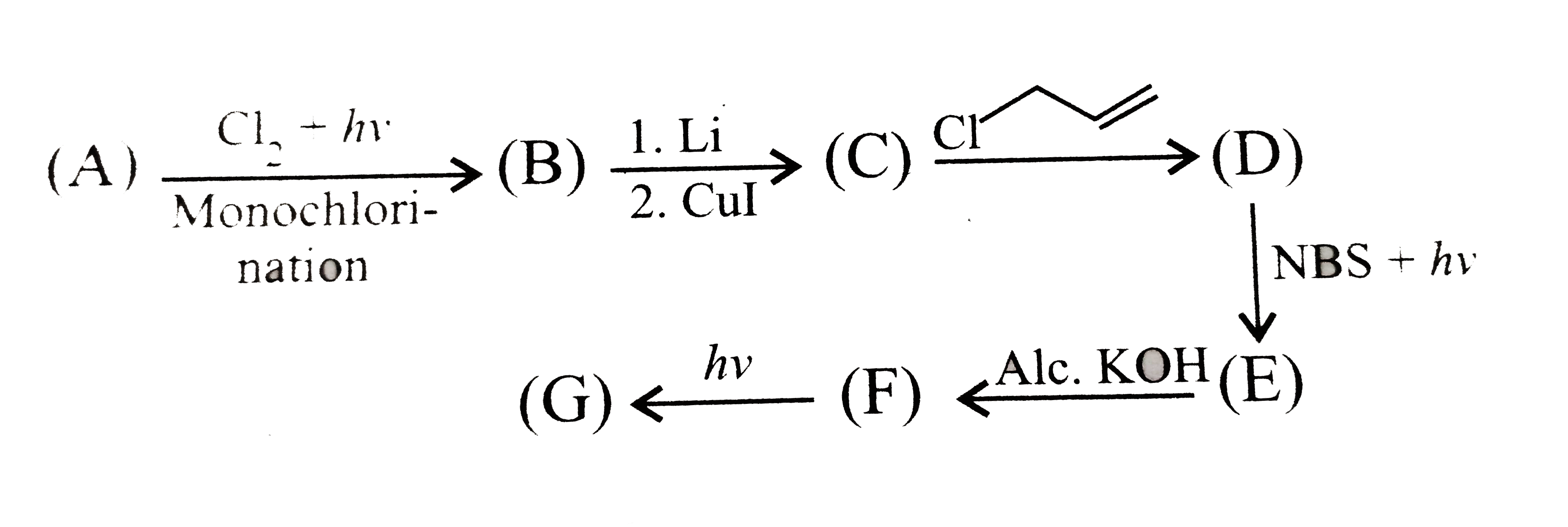
Compound (C) is:View Solution

