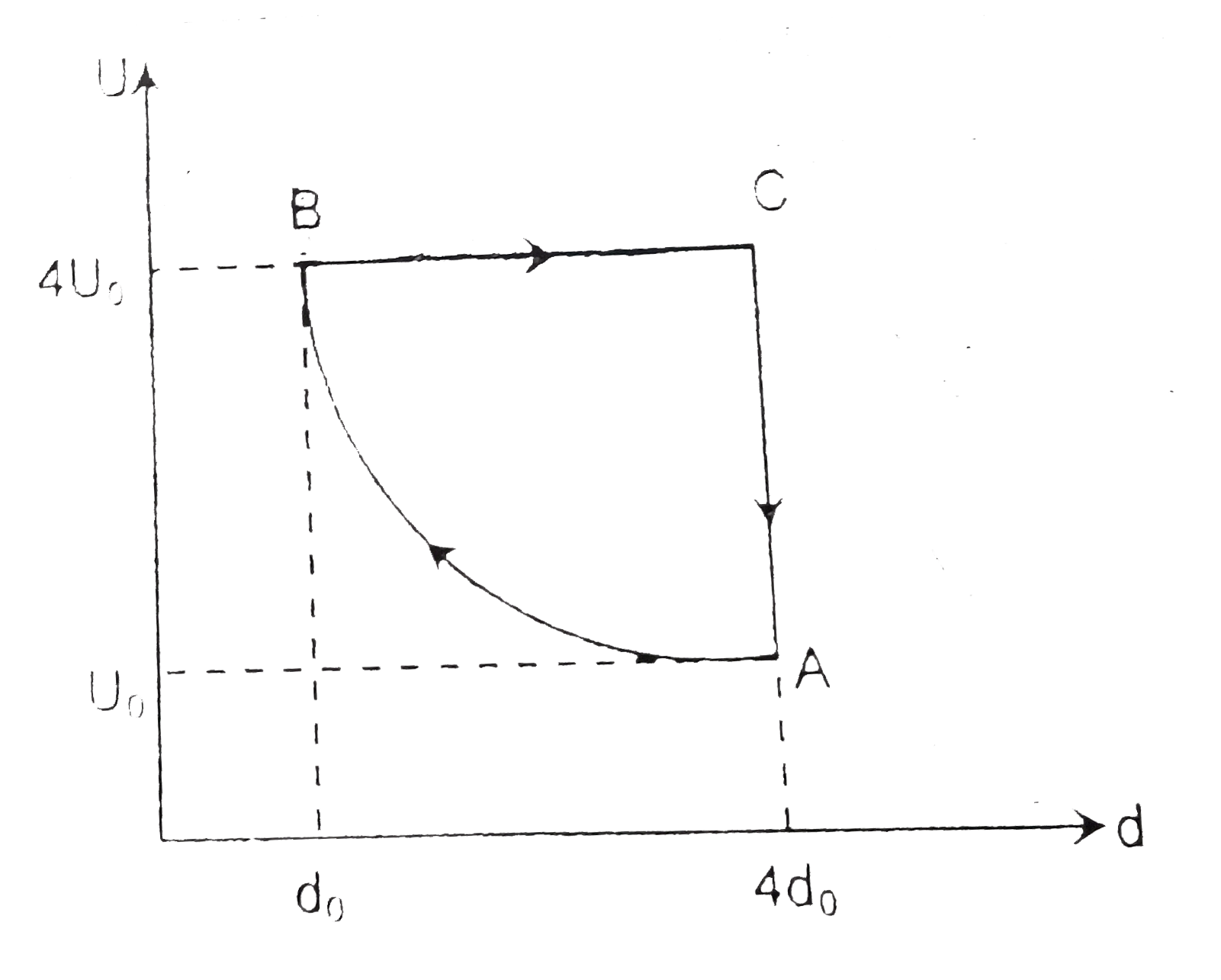
The variation of internal energy U and density d of one mole of an ideal monatomic gas is shown inn cyclic process ABCA. The curve from A to B is a rectangular hyperbola. Select correct alternatives.
The work done by gas in process AB is 2U0
The work done by gas in process BC is −3U02ln2
The molar heat capacity of gas for process CA is 3R2
The molar heat capacity of gas for process AB is 3R2
The correct Answer is:A, C
PM=dRT
in ABd∝1T therefore it is an isoberic process.
WAR=nRΔT=R(4T0−T0)
U0=32RT0
WAB=2U0
In process BC (isothermal)
WBC=−nR(4T0)ln(4d0d0)=−8RT0ln2
=−163U0ln2
Process CA is isochoric while AB is isobaric
Similar Questions
Figure shows the variations of the internal energy U With density ρ one mole an ideal monatomic gas for thermodynamic cycle ABCA . Here process AB is a part of rectangular hyperbola,-
_S01_092_Q01.png) View Solution
View SolutionOne mole of an ideal monoatomatic gas is taken round the cylic process ABCA as shown Then
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
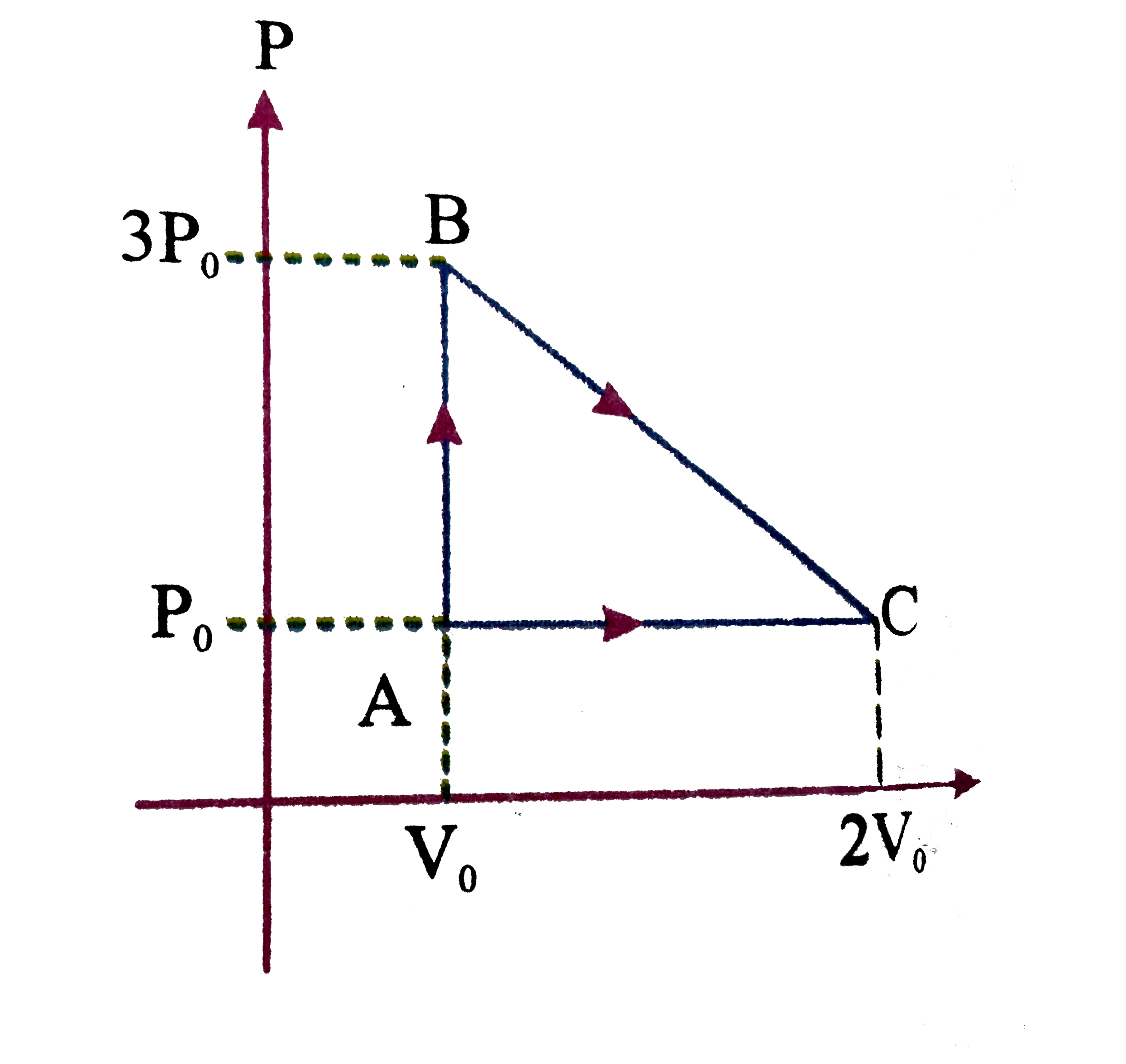
A thermodynamic process of one mole ideal monoatomic gas is shown in figure. The efficiency of cyclic process ABCA will be
A0.25B0.125C0.5D0.077
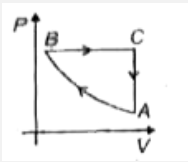
A cyclic process on an ideal monatomic gas is shown in figure . The correct statement is
 View Solution
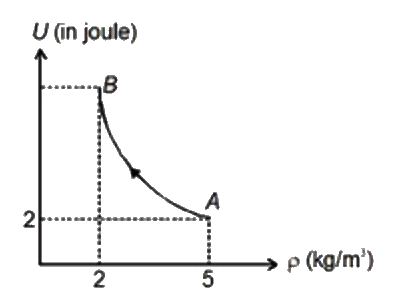
View SolutionFigure shows the variation of the internal energy U with the density ρ of an ideal monoatomic gas for a therodynamic process AB. Process AB is a part of arectangular hyperbola. Find the work done (in joule) by gas in process AB.
 View Solution
View SolutionOne mole of an ideal mono-atomic gas is taken round cyclic process ABC as shown in figure below. Calculate work done
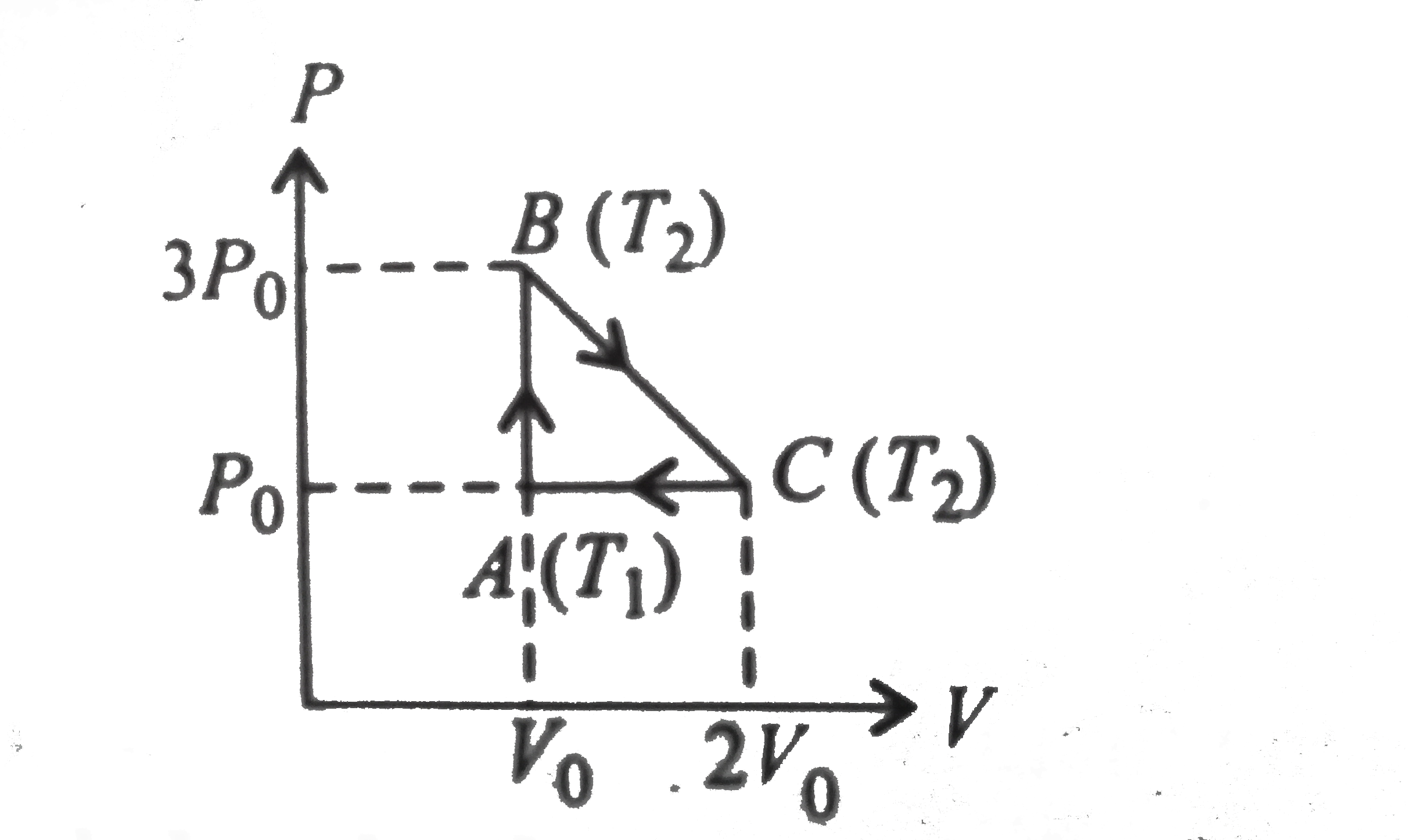 View Solution
View SolutionOne mole of an ideal mono-atomic gas is taken round cyclic process ABC as shown in figure below. Calculate work done
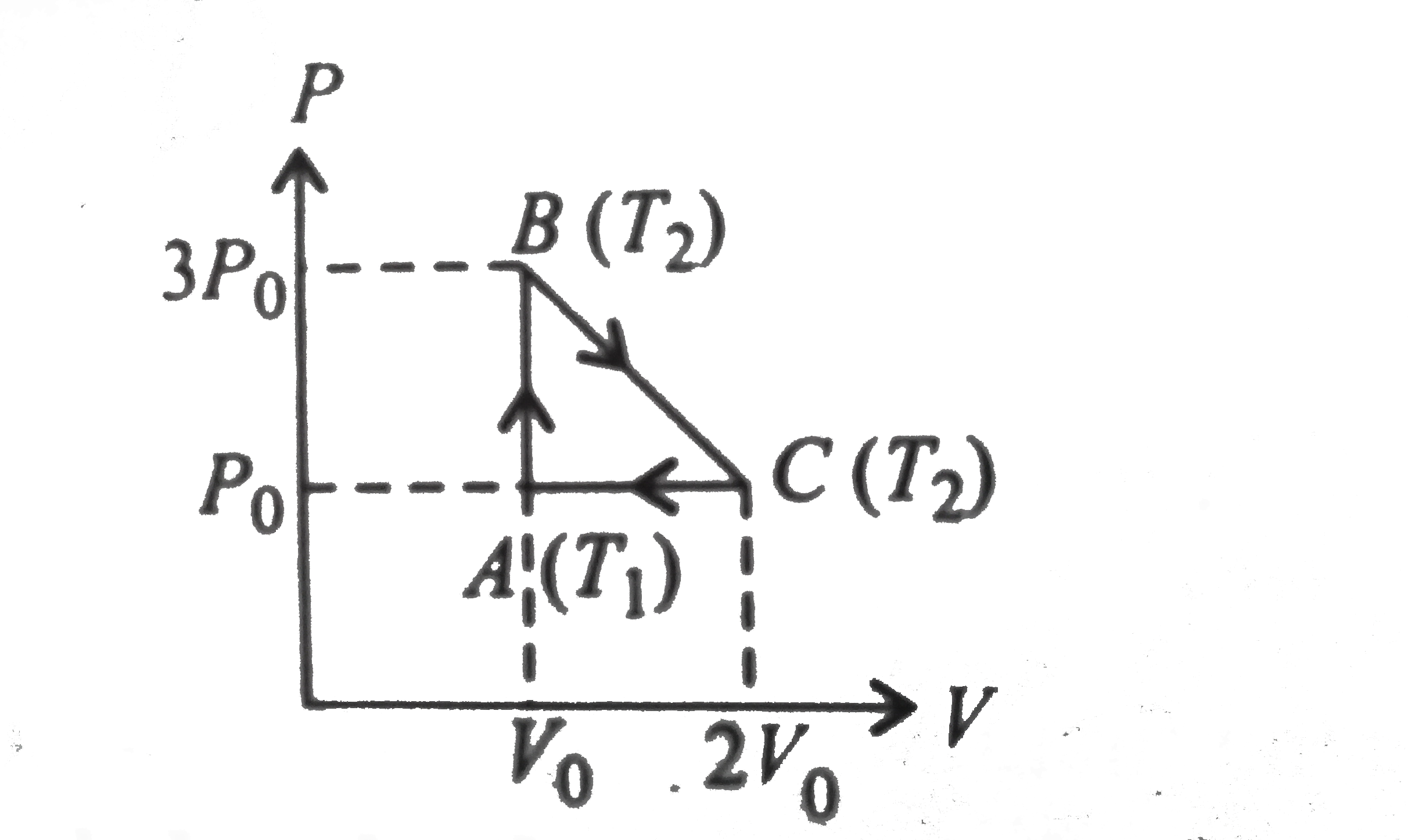 View Solution
View SolutionWhich one is not correct for a cyclic process as shown in the figure ?
 View Solution
View SolutionA thermodynamic process of one mole ideal monoatomic gas is shown in figure. The efficiency of cyclic process ABCA will be

View SolutionOne mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).
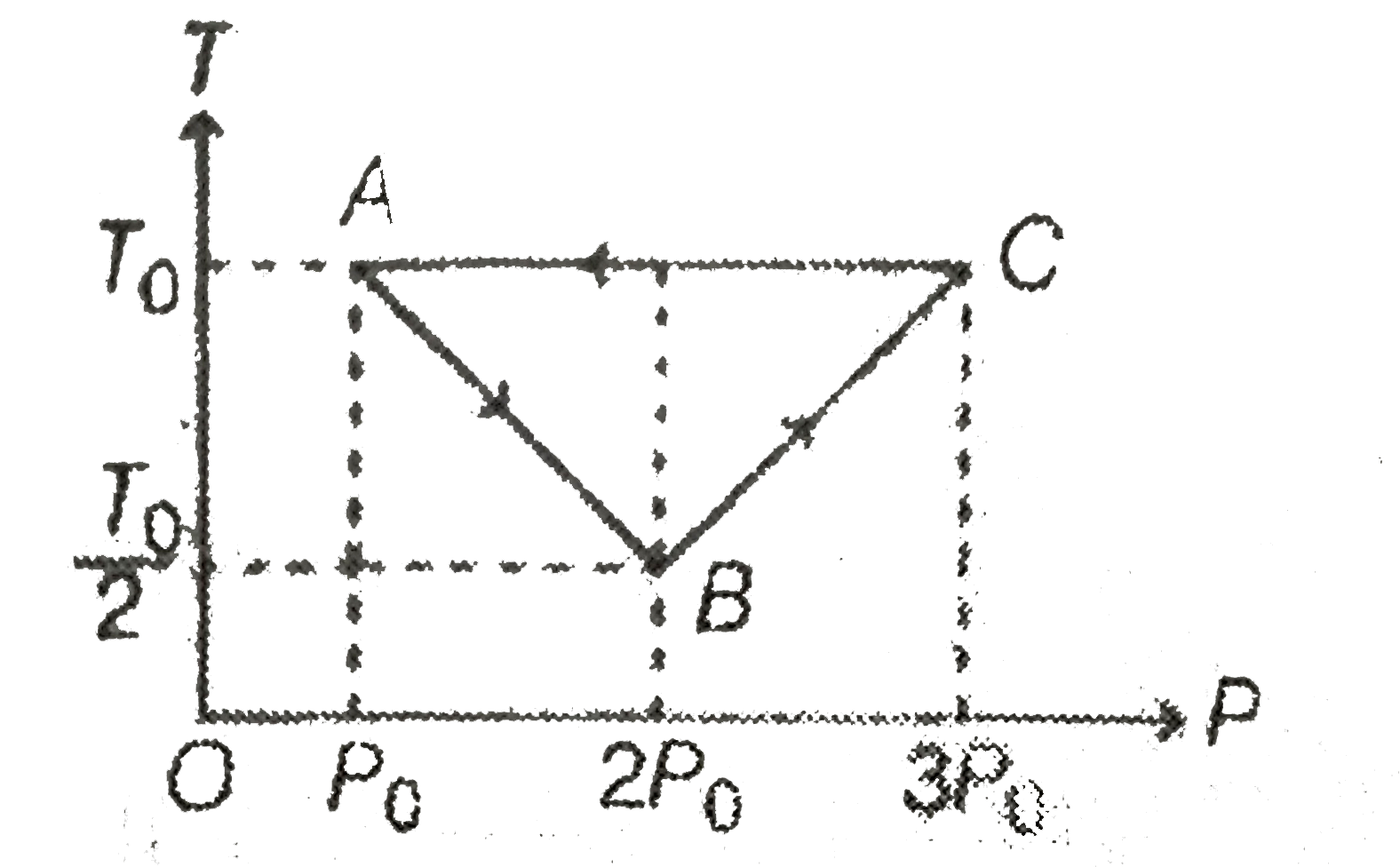 View Solution
View Solution

