Which of the following figure represents are correct solution of the equation sin−1xcos−1y=0?
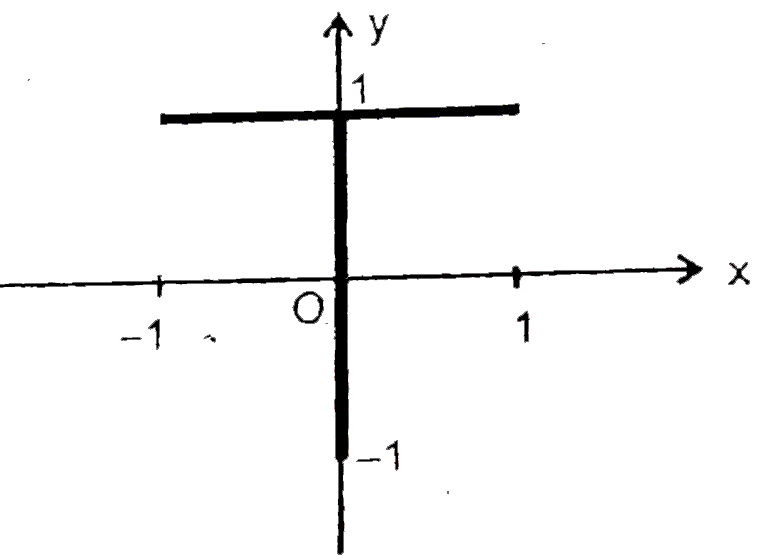


The correct Answer is:A
To solve the equation sin−1xcos−1y=0, we can follow these steps:
Step 1: Understand the equation
The equation sin−1xcos−1y=0 implies that the product of two terms is zero. This means that at least one of the terms must be zero.
Step 2: Set each term to zero
We can set each term in the product to zero:
1. sin−1x=0
2. cos−1y=0
Step 3: Solve sin−1x=0
To solve sin−1x=0:
- The value of x for which sin−1x=0 is when x=sin(0∘).
- Therefore, x=0.
Step 4: Solve cos−1y=0
To solve cos−1y=0:
- The value of y for which cos−1y=0 is when y=cos(0∘).
- Therefore, y=1.
Step 5: Identify the solution set
From the above steps, we have:
- x=0 (which corresponds to the y-axis)
- y=1 (which corresponds to the horizontal line at y=1)
Step 6: Graph the solution
Now we can graph these solutions:
- The line x=0 is the y-axis.
- The line y=1 is a horizontal line that intersects the y-axis at y=1.
Conclusion
The correct representation of the solution to the equation sin−1xcos−1y=0 is the intersection of the y-axis and the line y=1.
The equation sin−1xcos−1y=0 implies that the product of two terms is zero. This means that at least one of the terms must be zero.
We can set each term in the product to zero:
1. sin−1x=0
2. cos−1y=0
To solve sin−1x=0:
- The value of x for which sin−1x=0 is when x=sin(0∘).
- Therefore, x=0.
To solve cos−1y=0:
- The value of y for which cos−1y=0 is when y=cos(0∘).
- Therefore, y=1.
From the above steps, we have:
- x=0 (which corresponds to the y-axis)
- y=1 (which corresponds to the horizontal line at y=1)
Now we can graph these solutions:
- The line x=0 is the y-axis.
- The line y=1 is a horizontal line that intersects the y-axis at y=1.
The correct representation of the solution to the equation sin−1xcos−1y=0 is the intersection of the y-axis and the line y=1.
Similar Questions
Knowledge Check
Which of the following is a solution to the equation y=√15−y+3?
I.-1
II. 6
III. 11AII onlyBIII onlyCI and II onlyDII and III only
Which of the following is the solution set of the equation sin−1x=cos−1x+sin−1(3x−2)
View SolutionWhich of the following is correct sin1∘>sin1
View SolutionWhich of the following figures does not represent 1 mole of dioxygen gas at STP ?
View SolutionNumber of possible solution for the equation sin−1x+cos−1y=11π2 is / are
View SolutionThe solution set of the equation
cos−1x−sin−1x=sin−1(1−x) is
View SolutionThe number of solution (s) of the equation sin−1x+cos−1(1−x)=sin−1(−х) is/are
View SolutionSolve the equation: 2sin3ydx+3xcos3ydy=0
View Solution
