Consider a cell of emf E and internal resistance r. The current drawn (i) from cell can be varied output power from cell is same when current drawn is i1=2A and i2=8A. For what value of current the output power wwill be maximum.
To solve the problem, we need to find the value of current at which the output power from the cell is maximum. We are given two currents, i1=2A and i2=8A, for which the output power is the same.
1. Understanding the Power Formula:
The power P delivered by the cell can be expressed as:
P=E⋅I−I2⋅r
where E is the emf of the cell, I is the current, and r is the internal resistance.
2. Setting Up Equations for Given Currents:
For i1=2A:
P1=E⋅2−(22)⋅r=2E−4r
For i2=8A:
P2=E⋅8−(82)⋅r=8E−64r
Since P1=P2, we can equate the two expressions:
2E−4r=8E−64r
3. Solving for E and r:
Rearranging the equation:
64r−4r=8E−2E
60r=6E
Dividing both sides by 6:
10r=E
4. Finding Maximum Power:
The power can be rewritten as:
P=E⋅I−I2⋅r
Substituting E=10r:
P=10r⋅I−I2⋅r
P=r(10I−I2)
5. Maximizing Power:
To find the maximum power, we differentiate P with respect to I and set the derivative to zero:
dPdI=r(10−2I)=0
Setting the equation to zero:
10−2I=0
Solving for I:
2I=10⟹I=5A
Final Answer:
The value of current at which the output power will be maximum is I=5A.
The power P delivered by the cell can be expressed as:
P=E⋅I−I2⋅r
where E is the emf of the cell, I is the current, and r is the internal resistance.
For i1=2A:
P1=E⋅2−(22)⋅r=2E−4r
For i2=8A:
P2=E⋅8−(82)⋅r=8E−64r
Since P1=P2, we can equate the two expressions:
2E−4r=8E−64r
Rearranging the equation:
64r−4r=8E−2E
60r=6E
Dividing both sides by 6:
10r=E
The power can be rewritten as:
P=E⋅I−I2⋅r
Substituting E=10r:
P=10r⋅I−I2⋅r
P=r(10I−I2)
To find the maximum power, we differentiate P with respect to I and set the derivative to zero:
dPdI=r(10−2I)=0
Setting the equation to zero:
10−2I=0
Solving for I:
2I=10⟹I=5A
The value of current at which the output power will be maximum is I=5A.
Similar Questions
A cell of emf ε and internal resistance r is charged by a current I, then
View SolutionThe electric current drawn from cell is
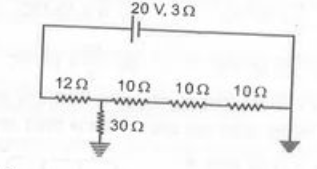
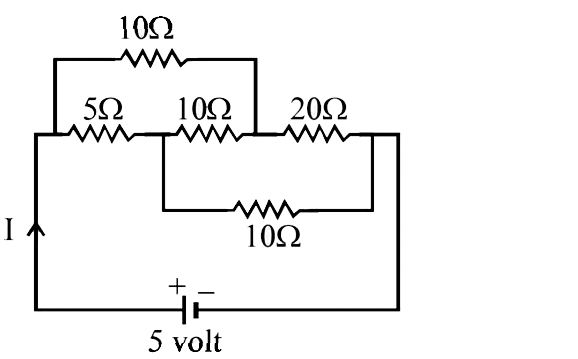
View SolutionThe current I drawn from the 5 volt source will be
View SolutionA cell of emf 'E' and internal resistance 'r' draws a current 'I'. Write the relation between terminal voltage 'V' in terms of E, I and r.
View SolutionWhat transformation of energy takes place when current is drawn from a cell ?
View SolutionA cell of emf 16V and internal resistant 4Ω can deliver maximum power to a load of resistance R where R is equal to
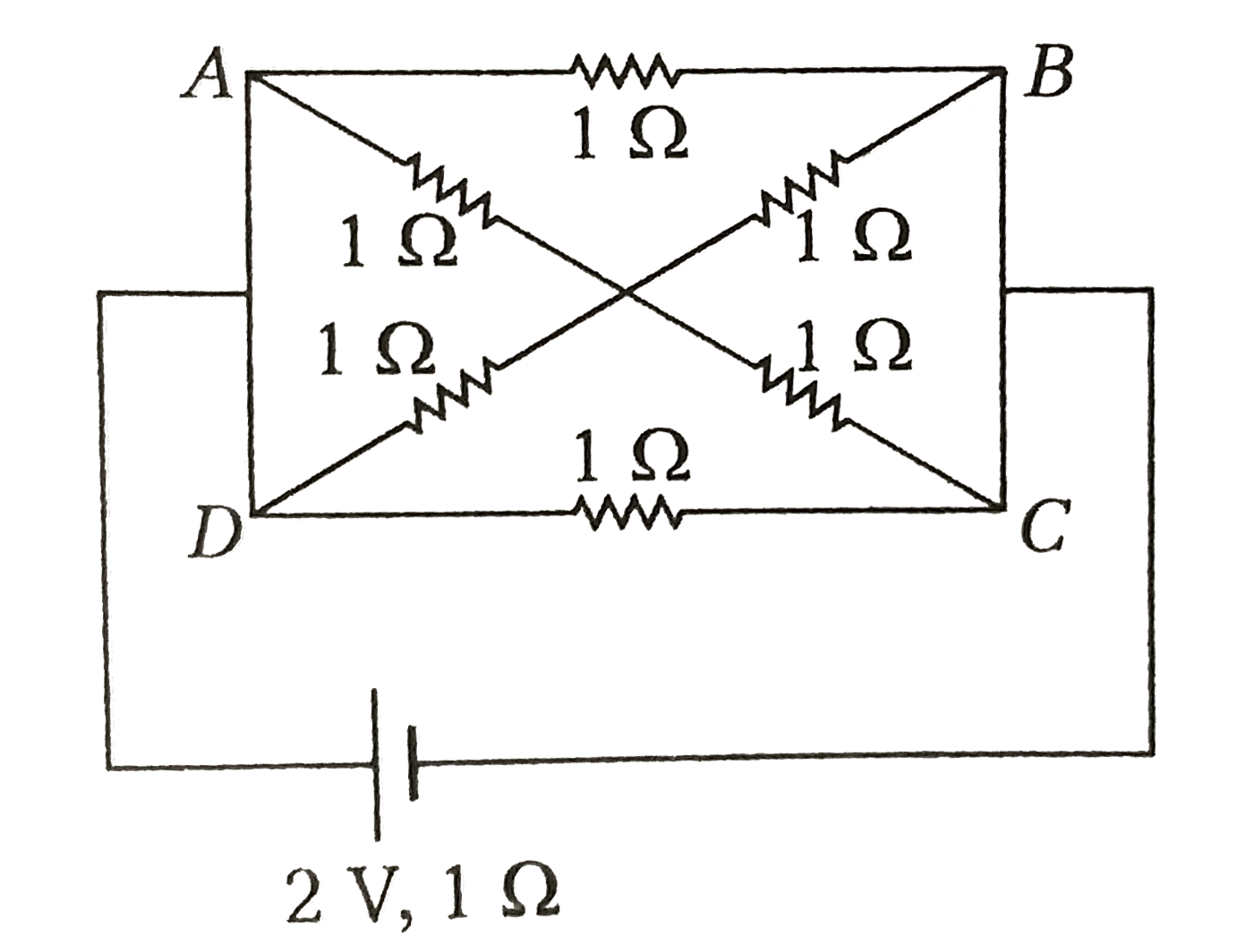
View SolutionFind the current drawn from a cell of emf 2 V and internal resistance 2Ω connected to the network given below.
View SolutionA cell of emf ε and internal resistance r is connected across a load resistance R
(i) Find the maximum power delivered at the load ?
.
View SolutionCurrent I is being driven through a cell of emf E and internal resistance r as shown in the figure. Choose the following correct statements.

View SolutionWhen capacitor is fully charged, find current drawn from the cell.
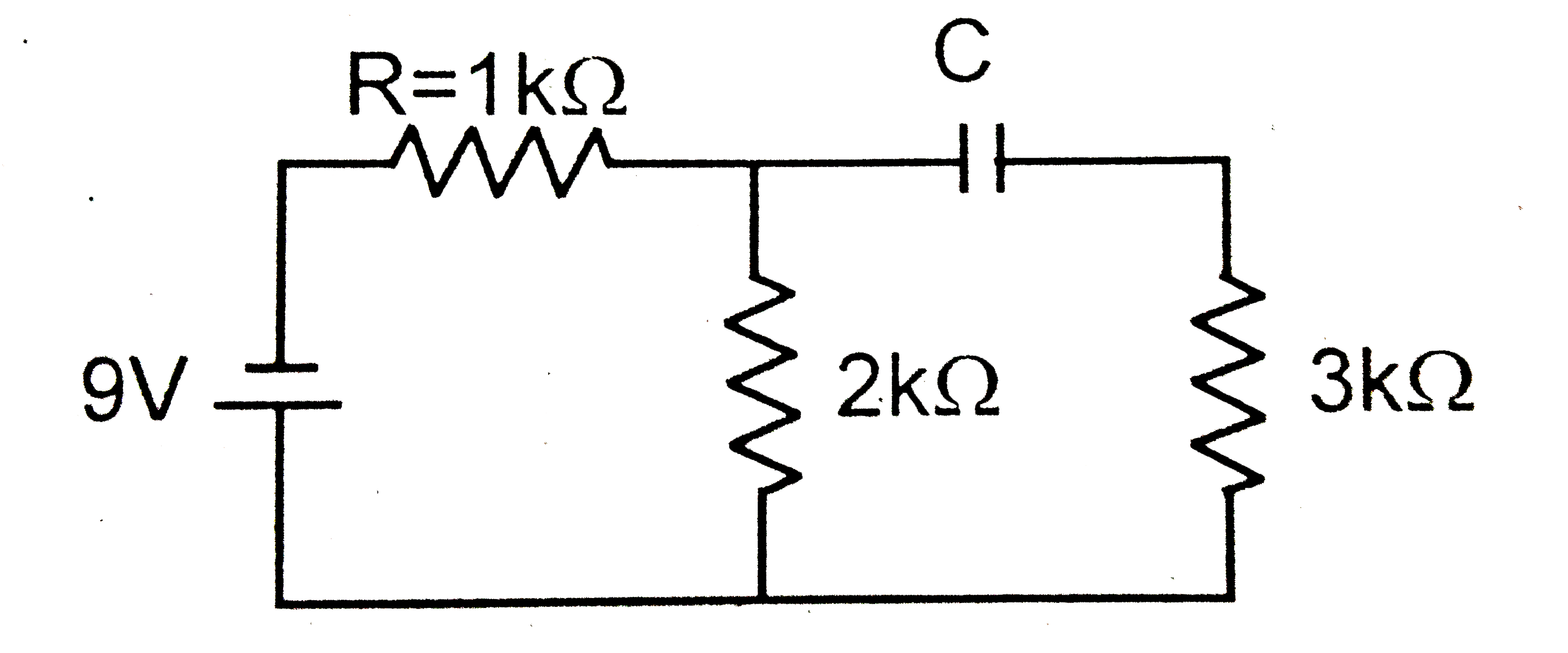
View Solution
