A mono atomic gas adsorbed on a surface follows. Langmuir adsorption isotherm. A plot of the fraction of source coverage , against concentration of the gas , for very low concentration of gas, is described by the equation.
To solve the problem regarding the Langmuir adsorption isotherm for a monoatomic gas X, we will follow these steps:
Step 1: Understand the Langmuir Adsorption Isotherm
The Langmuir adsorption isotherm describes the relationship between the pressure (or concentration) of a gas and the fraction of the surface that is covered by the adsorbed gas. The equation is given by:
θ=KP1+KP
where:
- θ is the fraction of the surface coverage,
- K is the equilibrium constant,
- P is the partial pressure of the gas.
Step 2: Relate Pressure to Concentration
For gases, the partial pressure P can be related to concentration C using the ideal gas law. Specifically, at constant temperature, we have:
P∝C
This means we can express P in terms of concentration C:
P=kC
where k is a proportionality constant.
Step 3: Substitute Concentration into the Langmuir Equation
Substituting P=kC into the Langmuir equation gives us:
θ=K(kC)1+K(kC)
Step 4: Simplify for Very Low Concentration
For very low concentrations of the gas X, the term K(kC) becomes very small. Therefore, we can approximate the denominator:
1+K(kC)≈1
Thus, the equation simplifies to:
θ≈K(kC)
Step 5: Final Form of the Equation
Let A=Kk (a constant), we can rewrite the equation as:
θ≈AC
This indicates that at very low concentrations, the fraction of surface coverage θ is directly proportional to the concentration C.
Conclusion
The final equation that describes the relationship between the fraction of surface coverage θ and the concentration of the gas X for very low concentrations is:
θ≈AC
The Langmuir adsorption isotherm describes the relationship between the pressure (or concentration) of a gas and the fraction of the surface that is covered by the adsorbed gas. The equation is given by:
- θ is the fraction of the surface coverage,
- K is the equilibrium constant,
- P is the partial pressure of the gas.
For gases, the partial pressure P can be related to concentration C using the ideal gas law. Specifically, at constant temperature, we have:
Substituting P=kC into the Langmuir equation gives us:
For very low concentrations of the gas X, the term K(kC) becomes very small. Therefore, we can approximate the denominator:
Let A=Kk (a constant), we can rewrite the equation as:
The final equation that describes the relationship between the fraction of surface coverage θ and the concentration of the gas X for very low concentrations is:
Similar Questions
According to Langmuir adsorption isotherm, the amount of gas adsorbed at very high pressure:
View SolutionAccording of Langmuir adsorption isotherm amount of gas adsorbed at very low pressure
View SolutionA gas undergoes physical adsorption on a surface and follows the givn Freundlich adsoprtion isotherm equation xm=kp0.5. Adsorption of the gas increases with:
View SolutionA gas undergoes physical adsorption on a surface and follows the givn Freundlich adsoprtion isotherm equation xm=kp0.5. Adsorption of the gas increases with:
View SolutionAdsorption of gas follows Freundlich adsorption isotherm. If x is the mass of the gas adsorbed on mass m of the adsrobent , the correct plot of xm versus p is :
View SolutionAdsorption of a gas follows Freundlich adsorption isotherm. In the given plot,x is the mass of the gas adsorbed on mass m of the adsorbent at pressure P. xm is proportional to:
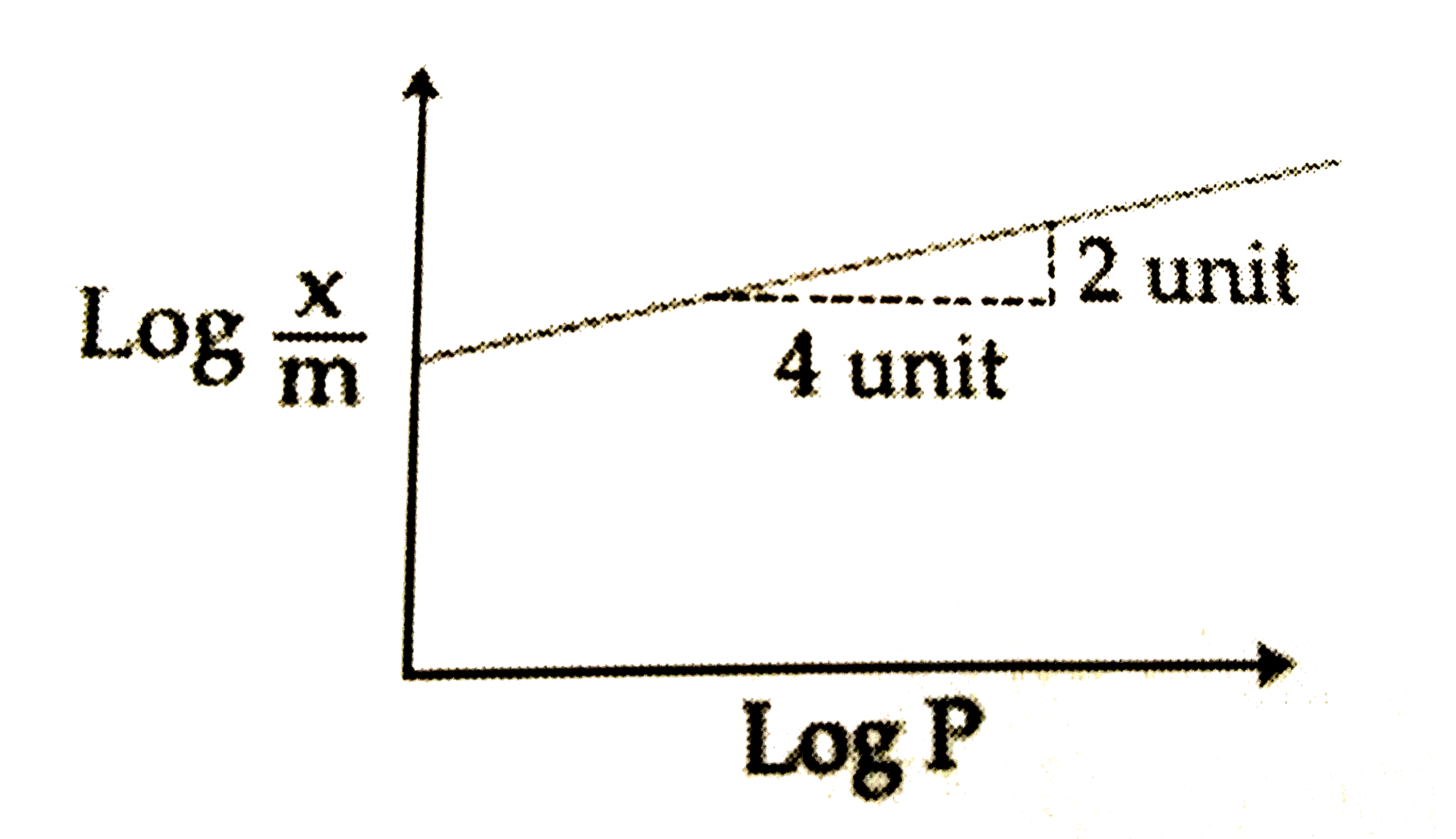
View SolutionAdsorption of a gas follows Freundlich adsorption isotherm. In the given plot,x is the mass of the gas adsorbed on mass m of the adsorbent at pressure P. xm is proportional to:
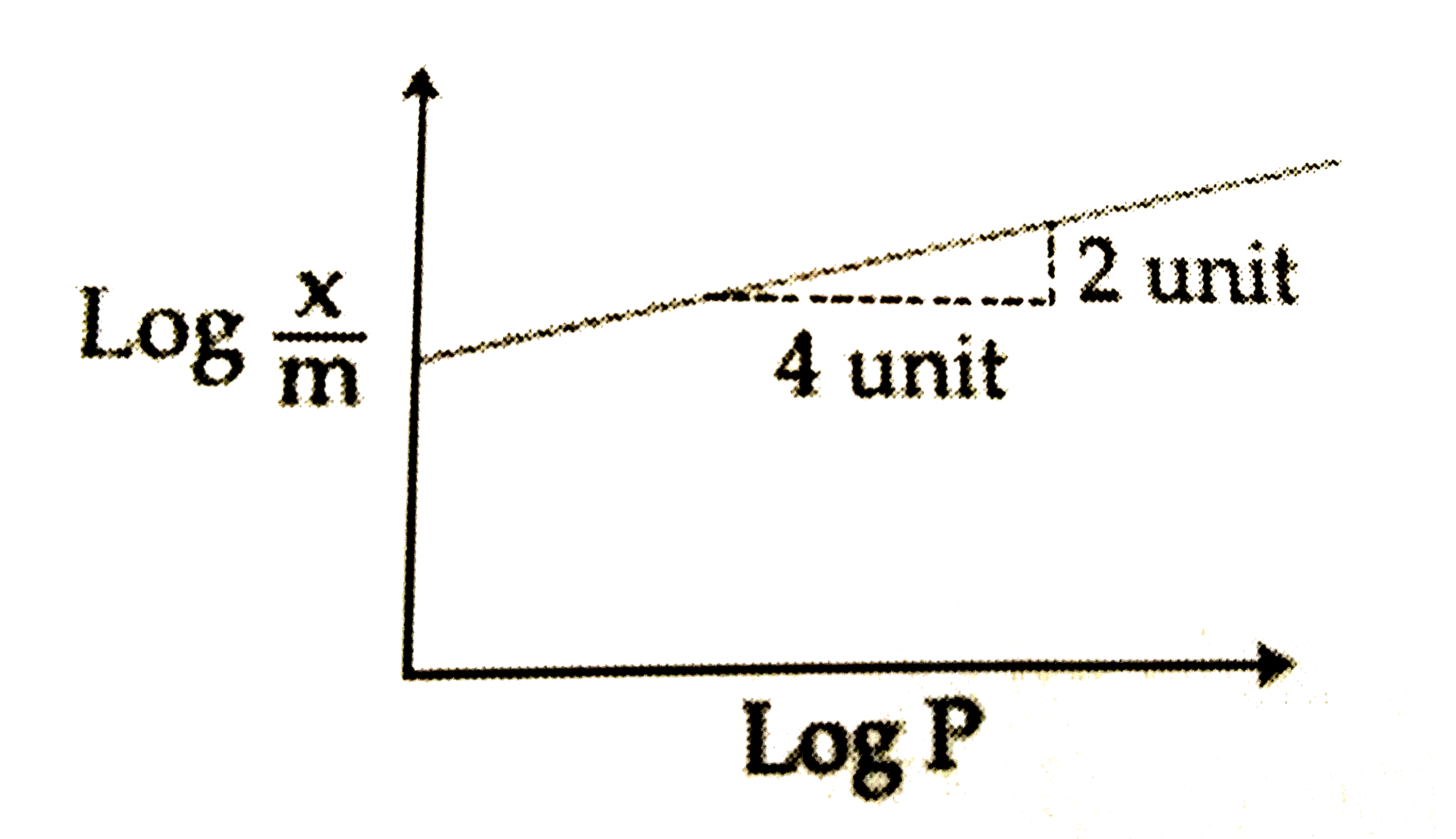
View SolutionAdsorption of a gas on a surface follows Freundlich adsorption isotherm. Plot of log xm versus log P gives a straight line with slope equal to 0.5, then :
(xm is the mass of the gas adsorbed per gram of adsorbent)
View SolutionAdsorption of gas follows Freundlich adsorption isotherm. x is the mass of the gas adsorbed on mass m of the adsorbent. The plot of logxm versus log p is shown in the given graph.
xm is proportional to:

View SolutionAdsorptionof a gas follows Freundlich adsorption isotherm. x is the mass of the gas adsorbed on mass m of the adsorbent.
The plot of logxm versus log p is shown in the given graph xm is proportional to :
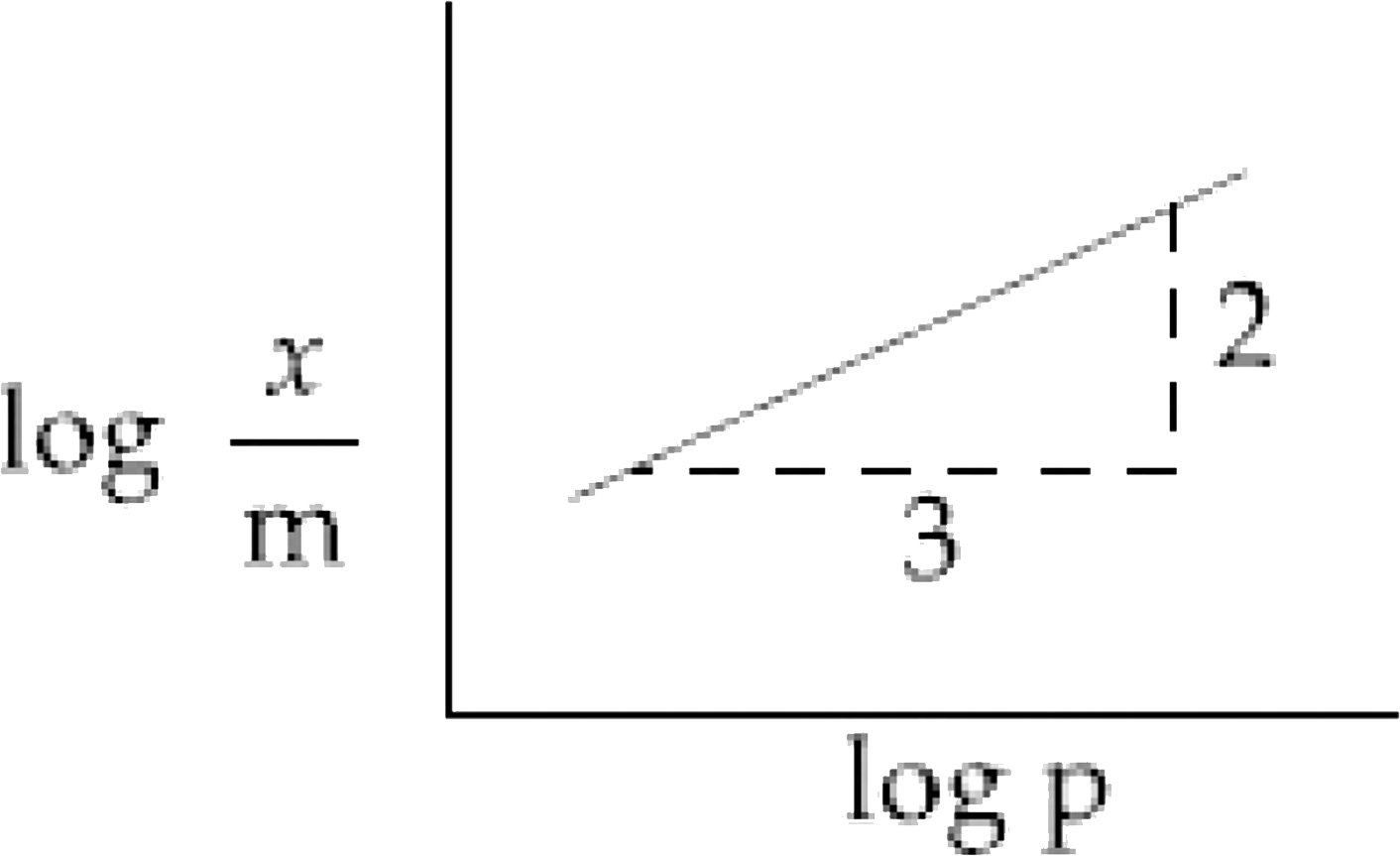
View Solution
