Which of the following are correct ?
graph of y=2log2x is 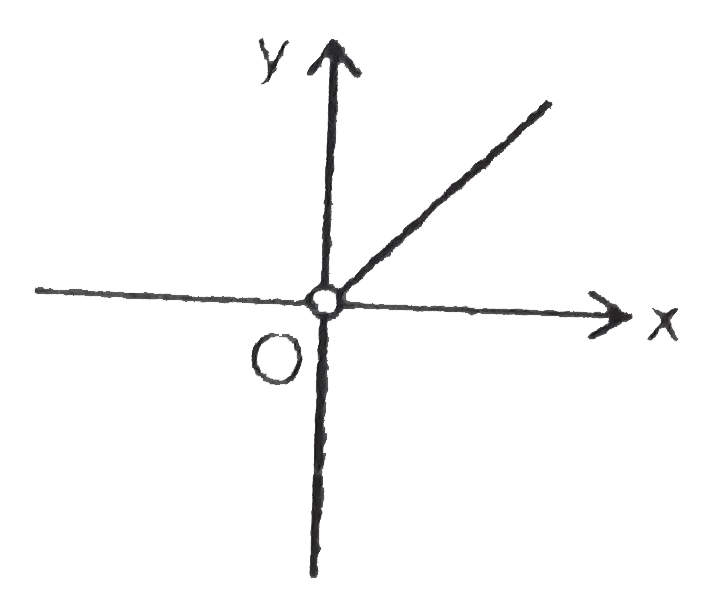
graph of y=xlogx2 is 
graph of y=2log2x2 is 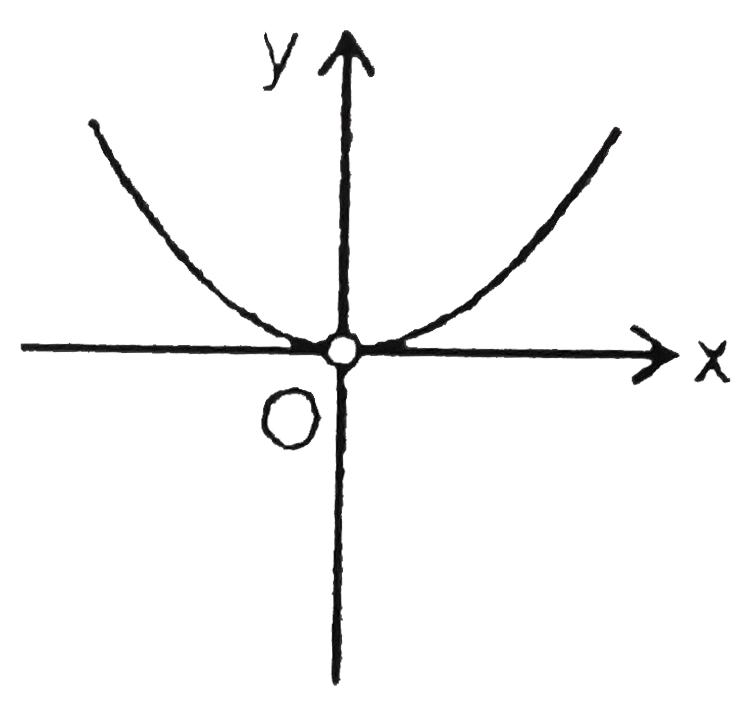
graph of y=22log2x is 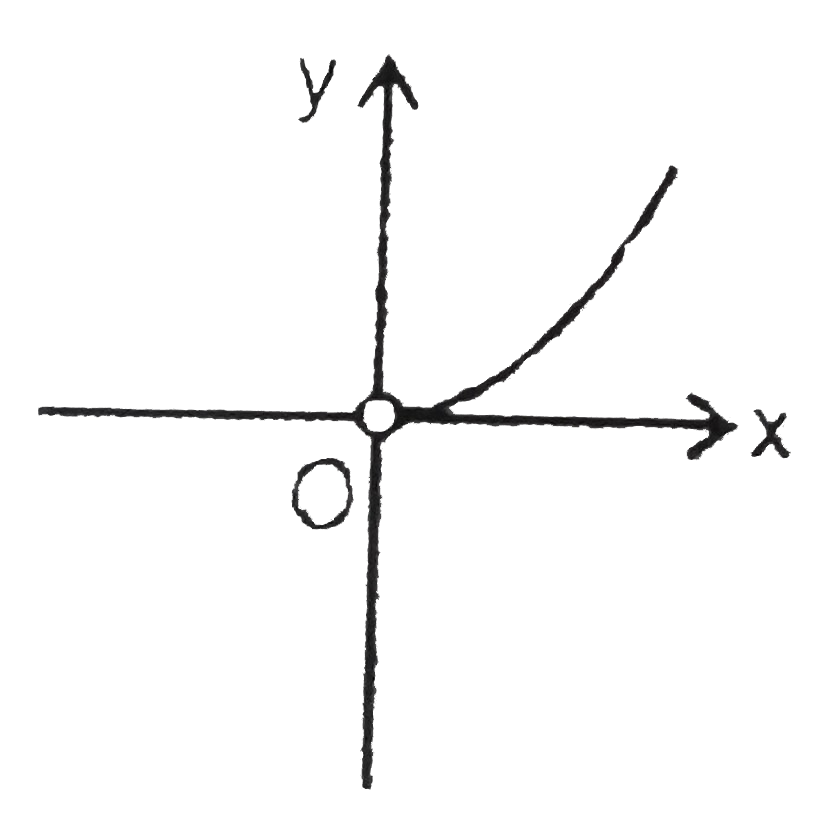
The correct Answer is:A,B,C,D
To solve the question of determining which of the given graphs are correct, we will analyze each option step by step using logarithmic properties.
1. Option 1: y=2logx
- Using the property alogmn=nlogma, we can rewrite:
y=2logx=log(x2)
- This means y=log(x2) which implies x2>0. Therefore, x>0.
- The graph of y=x is a straight line through the origin, but since x must be greater than 0, the graph is valid for x>0.
- Conclusion: This graph is correct.
2. Option 2: y=xlog2x
- We can rewrite this using the property logmnp=plogmn:
y=xlog2x=2log2x=2
- Here, x must not equal 0 or 1 (since log2x is undefined at these points).
- The graph of y=2 is a horizontal line, which is valid except at x=0 and x=1.
- Conclusion: This graph is correct.
3. Option 3: y=2log2(x2)
- Using the logarithmic property, we can simplify:
y=2log2(x2)=2⋅2log2x=4log2x
- The graph of y=x2 is a parabola that opens upwards. The domain for x2 is all real numbers except x=0.
- Conclusion: This graph is correct.
4. Option 4: y=22log2x
- We can simplify this using the property of exponents:
y=22log2x=(2log2x)2=x2
- The graph of y=x2 is a parabola, and since x must be greater than 0 for the logarithm to be defined, the domain is x>0.
- Conclusion: This graph is correct.
Final Conclusion:
All options provided are correct.
- Using the property alogmn=nlogma, we can rewrite:
y=2logx=log(x2)
- This means y=log(x2) which implies x2>0. Therefore, x>0.
- The graph of y=x is a straight line through the origin, but since x must be greater than 0, the graph is valid for x>0.
- Conclusion: This graph is correct.
- We can rewrite this using the property logmnp=plogmn:
y=xlog2x=2log2x=2
- Here, x must not equal 0 or 1 (since log2x is undefined at these points).
- The graph of y=2 is a horizontal line, which is valid except at x=0 and x=1.
- Conclusion: This graph is correct.
- Using the logarithmic property, we can simplify:
y=2log2(x2)=2⋅2log2x=4log2x
- The graph of y=x2 is a parabola that opens upwards. The domain for x2 is all real numbers except x=0.
- Conclusion: This graph is correct.
- We can simplify this using the property of exponents:
y=22log2x=(2log2x)2=x2
- The graph of y=x2 is a parabola, and since x must be greater than 0 for the logarithm to be defined, the domain is x>0.
- Conclusion: This graph is correct.
All options provided are correct.
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 1
1 Videos
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS
9 Videos
- TEST PAPERBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPEREXERCISE - MATHEMATICS
48 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - MATHEMATICS
132 Videos
Similar Questions
Knowledge Check
Which of the following is correct ?
Asin1∘>sin1Bsin1∘<sin1Csin1∘=sin1Dsin1∘=π180sin1
Which of the following is correct?
View SolutionWhich of the following is correct?
View SolutionWhich of the following is correct?
View SolutionWhich of the following is correct
View SolutionWhich of the following is correct ?
View SolutionWhich of the following is correct?
View SolutionWhich of the following is correct.
View Solution
