A spherical tank of radius 0.35m is half filled with oil of relative density 0.8. if the tank is moving with a horizontal acceleration of 10ms2. The surface of oil is at rest with respect to sphere. The maximum gauge pressure of oil in the tank is n×103Pa, the value of n is approximately equal to (take g=10ms2
The correct Answer is:4
To solve the problem, we will follow these steps:
Step 1: Understand the System
We have a spherical tank of radius R=0.35m that is half-filled with oil of relative density ρr=0.8. The tank is accelerating horizontally with a=10m/s2.
Step 2: Calculate the Density of the Oil
The density of the oil can be calculated using the formula:
ρ=ρr×ρwater
where ρwater=1000kg/m3. Thus,
ρ=0.8×1000=800kg/m3
Step 3: Determine the Effective Gravitational Force
When the tank accelerates, the effective gravitational force acting on the oil is the vector sum of gravitational force and the pseudo force due to acceleration. The effective gravitational acceleration geffective can be calculated as:
geffective=√g2+a2
Substituting g=10m/s2 and a=10m/s2:
geffective=√102+102=√200=10√2m/s2
Step 4: Calculate the Maximum Depth of Oil
The maximum depth of the oil occurs at the bottom of the tank. Since the tank is half-filled, the depth h of the oil is:
h=R2=0.352=0.175m
Step 5: Calculate the Maximum Gauge Pressure
The maximum gauge pressure P at the bottom of the tank can be calculated using the formula:
P=ρ⋅geffective⋅h
Substituting the values:
P=800kg/m3⋅(10√2)m/s2⋅0.175m
Calculating this:
P=800⋅10√2⋅0.175
P=800⋅1.414⋅1.75≈800⋅2.449≈1959.2Pa
Step 6: Convert to Gauge Pressure in the Required Form
The problem states that the maximum gauge pressure can be expressed as n×103Pa. Thus,
P≈1959.2Pa≈1.9592×103Pa
So, n≈1.96.
Final Answer
Since we need to approximate n:
n≈2
We have a spherical tank of radius R=0.35m that is half-filled with oil of relative density ρr=0.8. The tank is accelerating horizontally with a=10m/s2.
The density of the oil can be calculated using the formula:
ρ=ρr×ρwater
where ρwater=1000kg/m3. Thus,
ρ=0.8×1000=800kg/m3
When the tank accelerates, the effective gravitational force acting on the oil is the vector sum of gravitational force and the pseudo force due to acceleration. The effective gravitational acceleration geffective can be calculated as:
geffective=√g2+a2
Substituting g=10m/s2 and a=10m/s2:
geffective=√102+102=√200=10√2m/s2
The maximum depth of the oil occurs at the bottom of the tank. Since the tank is half-filled, the depth h of the oil is:
h=R2=0.352=0.175m
The maximum gauge pressure P at the bottom of the tank can be calculated using the formula:
P=ρ⋅geffective⋅h
Substituting the values:
P=800kg/m3⋅(10√2)m/s2⋅0.175m
P=800⋅10√2⋅0.175
P=800⋅1.414⋅1.75≈800⋅2.449≈1959.2Pa
The problem states that the maximum gauge pressure can be expressed as n×103Pa. Thus,
P≈1959.2Pa≈1.9592×103Pa
So, n≈1.96.
Since we need to approximate n:
n≈2
Similar Questions
A spherical tank of 1.2m radius is half filled with oil of relative density 0.8. If the tank is given a horizontal acceleration of 10m/s2, the maximum pressure on the tank is √2P pascal. Find the value of P.
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
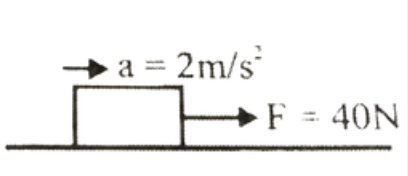
View SolutionThe velocity of kerosene oil in a horizontal pipe is 5m/s. If g=10m/s2 then the velocity head of oil wlill be
View SolutionA ball of mass 5.0 gm and relative density 0.5 strikes the surface of the water with a velocity of 20 m/sec. It comes to rest at a depth of 2m. Find the work done by the resisting force in water: (take g=10m/s2)
View SolutionAn open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
View SolutionAn iron ball of radius 0.3 cm falls through a column of oil of density 0.94 g cm−3. If it attains a terminal velocity of 0.54 m s−1, what is the viscosity of oil? Density of iron is 7.8 g cm−3
View SolutionA block of mass 1kg is at rest relative to a smooth wedge moving leftwards with constant acceleration a=5m/s−2 .Let N be the normal reation between the block and the wedge . Then (g=10m/s−2)

View SolutionA wheel of radius R=2m performs pure rolling on a rough horizontal surface with speed v=10 m/s . In the figure shown, angle θ is angular position of point P on wheel reaches the maximum height from ground. Find the value of secθ (take g=10m/s2).
View SolutionA solid sphere of mass m=2kg and density ρ=500kg/m3 is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water=1000kg/m3,g=10m/s2)

View SolutionA cylindrical vessel of radius 0.5 m is filled with oil at the rate of 0.25πm3/minute. The rate at which the surface of the oil is rising, is (a) 1 m/min. (b) 2 m/min. (c) 5 m/min. (d) 1.25 m/min.
View Solution
