A complex of iron and cyanide ions is 100%ionised ar 1m (molal). If its elevation in b.p.is 2.08 then the complex is (Kb=0.52∘mol−1kg),
K3[Fe(CN)6]
Fe(CN)2
K4[Fe(CN)6]
Fe(CN)4
The correct Answer is:A
To solve the problem, we need to determine the complex of iron and cyanide ions based on the given information about the boiling point elevation. Let's break down the solution step by step.
Step 1: Understand the Formula for Boiling Point Elevation
The formula for boiling point elevation (ΔTb) is given by:
ΔTb=Kb⋅m⋅i
where:
- ΔTb = elevation in boiling point
- Kb = ebullioscopic constant
- m = molality of the solution
- i = Van't Hoff factor (number of particles the solute dissociates into)
Step 2: Identify Given Values
From the problem, we have:
- ΔTb=2.08°C
- Kb=0.52°C kg/mol
- m=1mol/kg
Step 3: Rearrange the Formula to Find i
We can rearrange the formula to solve for i:
i=ΔTbKb⋅m
Step 4: Substitute the Values
Now, we can substitute the values into the equation:
i=2.080.52⋅1
Step 5: Calculate i
Calculating the above expression:
i=2.080.52=4
Step 6: Interpret the Result
The Van't Hoff factor i=4 indicates that the complex dissociates into 4 ions in solution.
Step 7: Identify the Complex
Now we need to find a complex of iron that, when dissociated, gives a total of 4 ions.
1. Option 1: K3(Fe(CN)6)
- Dissociates into 3K+ and (Fe(CN)6)3−
- Total ions = 3+1=4
2. Other Options (if provided)
- We would check other complexes to see if they also yield 4 ions. However, since we have already found one that works, we can conclude.
Conclusion
The complex that corresponds to the given boiling point elevation and dissociates into 4 ions is K3(Fe(CN)6).
---
The formula for boiling point elevation (ΔTb) is given by:
ΔTb=Kb⋅m⋅i
where:
- ΔTb = elevation in boiling point
- Kb = ebullioscopic constant
- m = molality of the solution
- i = Van't Hoff factor (number of particles the solute dissociates into)
From the problem, we have:
- ΔTb=2.08°C
- Kb=0.52°C kg/mol
- m=1mol/kg
We can rearrange the formula to solve for i:
i=ΔTbKb⋅m
Now, we can substitute the values into the equation:
i=2.080.52⋅1
Calculating the above expression:
i=2.080.52=4
The Van't Hoff factor i=4 indicates that the complex dissociates into 4 ions in solution.
Now we need to find a complex of iron that, when dissociated, gives a total of 4 ions.
- Dissociates into 3K+ and (Fe(CN)6)3−
- Total ions = 3+1=4
- We would check other complexes to see if they also yield 4 ions. However, since we have already found one that works, we can conclude.
The complex that corresponds to the given boiling point elevation and dissociates into 4 ions is K3(Fe(CN)6).
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - EXERCISE-1(PART-3)3videos
SOLUTIONS
- BOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - EXERCISE-2(PART-1)25videos
SOLUTIONS
- BOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - EXERCISE-1(PART-1)33videos
SOLUTIONS
- BOOK - RESONANCE ENGLISHCHAPTER - SOLUTION AND COLLIGATIVE PROPERTIESEXERCISE - PHYSICAL CHEMITRY (SOLUTION & COLLIGATIVE PROPERTIES)52videos
SOLUTION AND COLLIGATIVE PROPERTIES
- BOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART III : PRACTICE TEST-2 (IIT-JEE (ADVANCED PATTERN))23videos
STEREOISOMERISM
Similar Questions
Consider following figure and answer the questions at the end of it. Figure explains elevation in boiling point when a non-volatile solute is added to a solvent.
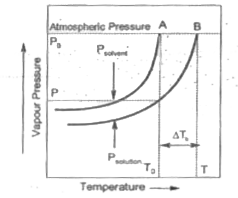
Variation of vapour pressure with temperature and showing elevation in boiling point.
A complex of iron and cyanide ions is 100% ionized at 1m (molal). If elevation in boiling point is 2.08∘(Kb=0.52∘mol−1kg) then the complex is:View SolutionFigure explains elevation in boiling point when a non-volatile solute is added to a solvent. Variation of vapour pressure with temperaure and elevation in boiling point is marked.

Elevation in b.p of an aqueous urea solution is 0.52∘(Kb=0.52∘mol−1kg). Hence, mole fraction of urea in this solution is:View Solution
Knowledge Check
- Question 1 - Select One
A solution containing 12.5 g of non-electrolyte substance in 185 g of water shows boiling point elevation of 0.80 K. Calculate the molar mass of the substance. (Kb=0.52Kkgmol−1)
A53.06 g mol−1B25.3 g mol−1C16.08 g mol−1D43.92 g mol−1
0.1 molal aqueous solution of an electrolyte AB3 is 90% ionised. The boiling point of the solution at 1 atm is (Kb(H2O)=0.52kg mol−1)
View Solution2.0 molal aqueous solution of an electrolyte X2Y3 is 75% ionised. The boiling point of the solution a 1 atm is (Kb(H2O)=0.52K kg mol−1)
View SolutionA solution containg 12g of a non-electrolyte substance in 52g of water gave boiling point elevation of 0.40K . Calculate the molar mass of the substance. (Kb for water =0.52Kkgmol−1)
View SolutionA solution of an organic compound is prepared by dissolving 30g in 100g water. Calculate the molecular mass of compound and the osmotic pressure of solution at 300K, when the elevation in boiling point is 0.52 and Kb for water is 0.52Km−1.
View SolutionA 0.1 molal solution of an acid is 4.5% ionized. Calculate freezing point. (molecular weight of the acid is 300 ). Kf=1.86 K mol−1kg.
View Solution3.0 molal aqueous solution of an electrolyte A2B3 is 50% ionised. The boilng point of the solution at 1 atm is: [kb(H2O)=0.52Kkgmol−1]
View SolutionA solid cube of edge length =25.32 mm of an ionic compound which has NaCl type lattice is added to 1kg of water.The boiling point of this solution is found to be 100.52∘C(assume 100% ionisation of ionic compound).If radius of anion of ionic solid is 200 pm then calculate radius of cation of solid in pm (picometer).
(Kb of water =0.52 K kg mole−1,Avogadro's number,NA=6×1023,(3√75)=4.22)View Solution

