Freundlich adsorption isotherm is given by the expression xm=kP1n which of the following conclusions can be draw from this expression?
When 1n=0, the adsorption is directly proportional to pressure
When n=1,xm vs p graph is a line parallel to x-axis
When 1n=0 the adsorption is independent of pressure
When n=2, plot off xm vs p is a rectangular hyperbola
The correct Answer is:C
To analyze the Freundlich adsorption isotherm given by the expression xm=kP1n, where x is the mass of the adsorbate, m is the mass of the adsorbent, P is the pressure, and k and n are constants, we can derive conclusions based on different values of n.
1. Understanding the Expression:
- The Freundlich adsorption isotherm expresses the relationship between the amount of adsorbate adsorbed per unit mass of adsorbent and the pressure of the adsorbate in the gas phase.
2. Analyzing the Case When 1n=0:
- If 1n=0, then n approaches infinity, and the expression simplifies to xm=k.
- This indicates that the adsorption is independent of pressure, meaning the amount adsorbed remains constant regardless of changes in pressure.
Conclusion: This statement is true.
3. Analyzing the Case When n=1:
- If n=1, then xm=kP.
- This is a linear relationship, and if we plot xm versus P, we get a straight line passing through the origin.
Conclusion: This statement is false, as the graph is not parallel to the x-axis.
4. Analyzing the Case When n=2:
- If n=2, then xm=kP12.
- This represents a square root relationship, which does not correspond to a rectangular hyperbola. Instead, it describes a parabolic curve.
Conclusion: This statement is false.
5. Final Conclusion:
- The only correct conclusion drawn from the expression is that when 1n=0, the adsorption is independent of pressure.
Summary of Conclusions:
- A: False (Adsorption is constant, not dependent on pressure)
- B: False (Graph is a line through the origin, not parallel to x-axis)
- C: True (Adsorption is independent of pressure when 1n=0)
- D: False (The plot is not a rectangular hyperbola)
- The Freundlich adsorption isotherm expresses the relationship between the amount of adsorbate adsorbed per unit mass of adsorbent and the pressure of the adsorbate in the gas phase.
- If 1n=0, then n approaches infinity, and the expression simplifies to xm=k.
- This indicates that the adsorption is independent of pressure, meaning the amount adsorbed remains constant regardless of changes in pressure.
- If n=1, then xm=kP.
- This is a linear relationship, and if we plot xm versus P, we get a straight line passing through the origin.
- If n=2, then xm=kP12.
- This represents a square root relationship, which does not correspond to a rectangular hyperbola. Instead, it describes a parabolic curve.
- The only correct conclusion drawn from the expression is that when 1n=0, the adsorption is independent of pressure.
- A: False (Adsorption is constant, not dependent on pressure)
- B: False (Graph is a line through the origin, not parallel to x-axis)
- C: True (Adsorption is independent of pressure when 1n=0)
- D: False (The plot is not a rectangular hyperbola)
Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following is equivalent to the expression x4−x3−x2?
Ax(x2−x−1)Bx(x−x2−x3)Cx(x3−x2)Dx2(x2−x−1)x2−10x−7
Which of the following expression is equivalent to the expression above ?A(x−5)2−32B(x−5)2+32C(x+5)2−32D(x+5)2+32The expression 3x−1x−4 is equivalent to which of the following ?
A12B3x−1x−4C3−11x−4D3+11x−4
The age pyramid for human population is shown below
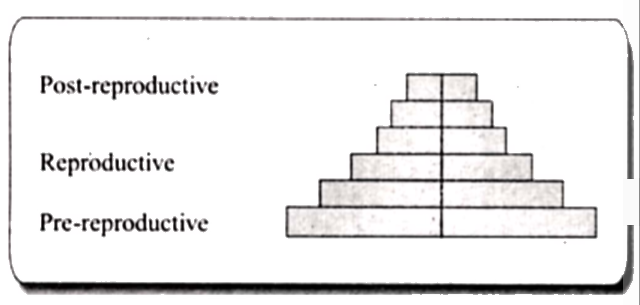
Which of the following conclusion can be drawn from the given age pyramid?
View SolutionExpress which of the following set ups can be used to verify
ohm's law?
View Solution√9x2
If x gt 0 , which of the following is equivalent to the given expression?
View Solution11x−4−1x+6
Which of the following is equivalent to the expression above?
View SolutionFor Freundlich adsorption isotherm, xm=kp1/n , the value of n is
View Solution
