If n1+n2+n3+n4=20 such that ni≥i+1∀i∈{1,2,3,4} and nin∈I then number of solutions are
a. 84
b. 126
c. 286
d.140
To solve the problem, we need to find the number of integer solutions to the equation:
n1+n2+n3+n4=20
with the constraints:
ni≥i+1for i=1,2,3,4
Step 1: Rewrite the variables
We can rewrite the variables ni in terms of new variables xi to simplify the problem. Let:
n1=x1+2n2=x2+3n3=x3+4n4=x4+5
This transformation is based on the constraints ni≥i+1.
Step 2: Substitute into the equation
Now substitute these expressions into the original equation:
(x1+2)+(x2+3)+(x3+4)+(x4+5)=20
Step 3: Simplify the equation
Combine like terms:
x1+x2+x3+x4+14=20
Subtract 14 from both sides:
x1+x2+x3+x4=6
Step 4: Identify the constraints on xi
Since ni must be greater than or equal to i+1, the new variables xi must satisfy:
x1≥0x2≥0x3≥0x4≥0
Step 5: Count the number of solutions
Now we need to find the number of non-negative integer solutions to the equation:
x1+x2+x3+x4=6
We can use the "stars and bars" theorem, which states that the number of ways to distribute n identical objects (stars) into r distinct boxes (variables) is given by:
(n+r−1r−1)
In our case, n=6 (the total we want to achieve) and r=4 (the number of variables):
Number of solutions=(6+4−14−1)=(93)
Step 6: Calculate the binomial coefficient
Now we calculate (93):
(93)=9!3!(9−3)!=9×8×73×2×1=5046=84
Final Answer
Thus, the number of solutions is:
84
We can rewrite the variables ni in terms of new variables xi to simplify the problem. Let:
Now substitute these expressions into the original equation:
Combine like terms:
Since ni must be greater than or equal to i+1, the new variables xi must satisfy:
Now we need to find the number of non-negative integer solutions to the equation:
Now we calculate (93):
Thus, the number of solutions is:
Topper's Solved these Questions
Similar Questions
Let N be the number of integer solutions of the equation n1+n2+n3+n4=17 when n≥1,n2≥−1,n3≥3,n4≥0. If N=17CK, then find K.
View SolutionLet n1<n2<n3<n4<n5 be positive integers such that n1+n2+n3+n4+n5=20. then the number of distinct arrangements n1,n2,n3,n4,n5 is
View SolutionIf n1, n2, n3,…..,n100 are positive real numbers such that n1+n2+n3+…+n100=20 and k=n1(n2+n3+n4)(n5+n6+…+n9)(n10+….+n16)…(…+n100), then k belongs to
View SolutionA coin is tossed. If head appears a fair die is thrown three times otherwise a biased die with probability of obtaining an even number twice as that of an odd number is thrown three times. If (n1,n2,n3) is an outcome, (1≤n1≤6) and is found to satisfy the equation in1+in2+in3=1, , then the probability that a fair die was thrown is (where i=√−1)
View SolutionA light passes through many parallel slans one by one as shown in figure.
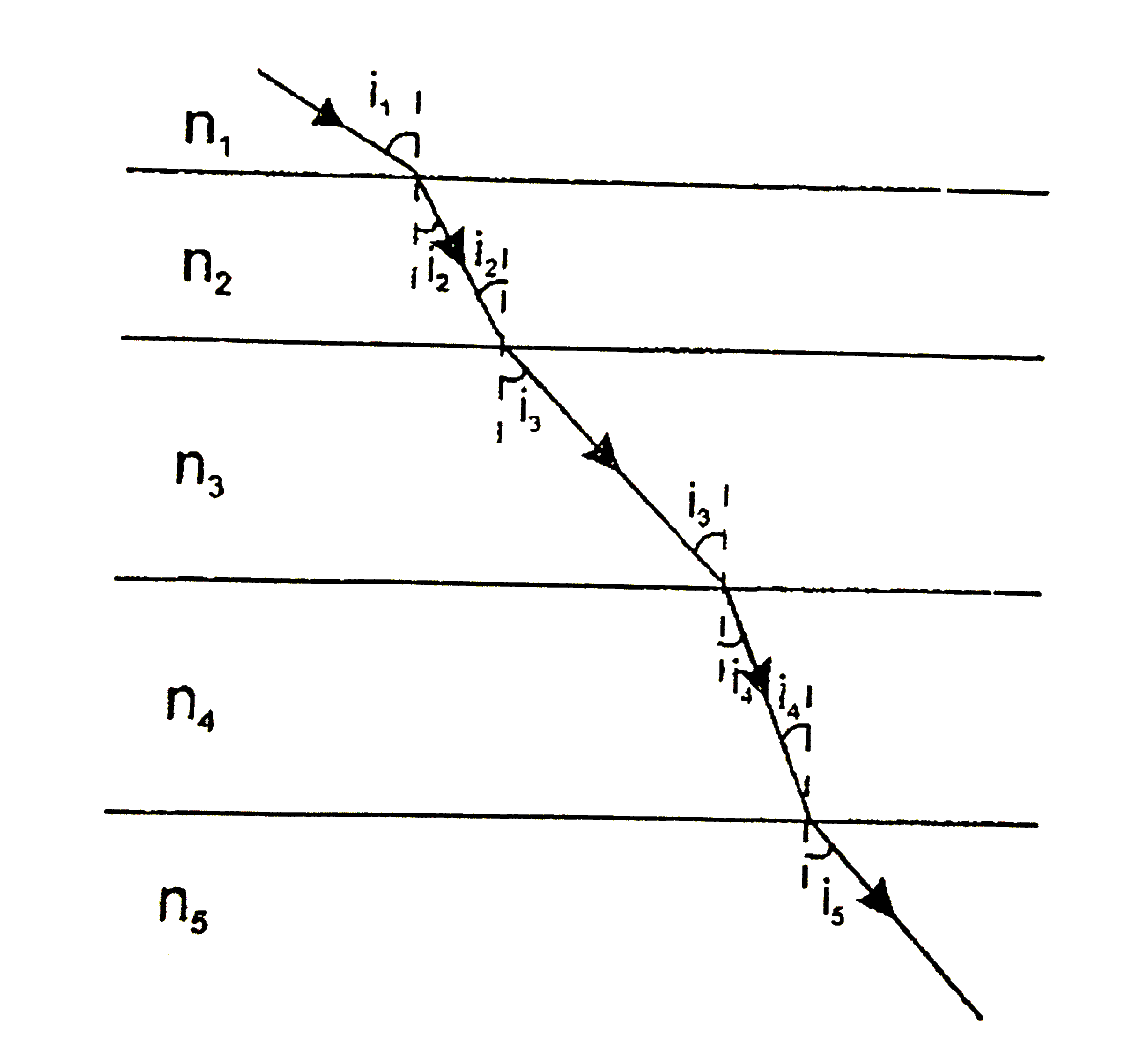
Prove that n1sini1=n2sini3sin=n4sini4=..... [Remember this]. Also prove that if n1=n4 then light rays in medium n1 and in medium n4 are parallel.
View Solutionin+in+1+in+2+in+3(n∈N) is equal to
View SolutionIf n∑i=1(xi+1)2=9n and n∑i=1(xi−1)2=5n, then standard deviation of these 'n' observations (x1) is: (1) 2√3 (2) √3 (3) √5 (4) 3√2
View SolutionFind the integral solution for n1n2=2n1−n2, where n1,n2∈integer.
View SolutionObserve the following statements :
(A) : 10 is the mean of a set of 7 obervations and 5 is the mean of a set of 3 observations. The mean of a combined set is 9.
(R ) : If ¯xi(i=1,2,…,k) are the means of k - series ni(I=1,2,3,…,k) respectively, then the combined or composite mean is
¯x=n1¯x1+n2¯x2+...+nk¯¯¯¯xkn1+n2+...+nk
View SolutionIf i=√−1, the number of values of i−n for a different n∈I is
View Solution
